Bài 14.5, 14.6, 14.7, 14.8 trang 34,35 SBT Vật lí 10
Giải bài 14.5, 14.6, 14.7, 14.8 trang 34,35 sách bài tập vật lý 10. Một vệ tinh có khối lượng m = 600 kg đang bay trên quỹ đạo tròn quan Trái Đất ở độ cao bằng bán kính Trái Đất. Biết Trái Đất có bán kín R = 6 400 km. Lấy g = 9,8 m/s2. Hãy tính
14.5.
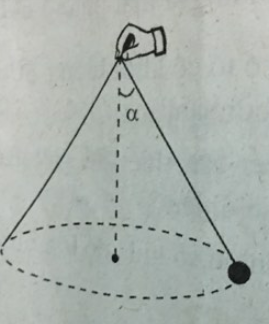
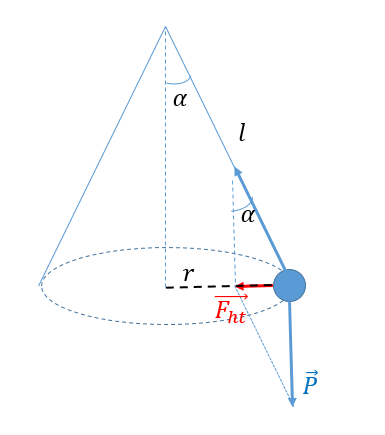
Trong thí nghiệm ở hình 14.1, quả cầu có khối lượng 30 g, dây dài 50 cm. Khi quả cầu quay với tần số 50 vòng/ phút thì \(\alpha \) có độ lớn gần bằng
A. \({43^0}\)
B. \({44^0}\)
C. \({45^0}\)
D. \({46^0}\)
Phương pháp giải:
\({F_{ht}} = m{\omega ^2}r\)
\(\omega = 2\pi f\)
Lời giải chi tiết:
\(f = 50vong/phut = \dfrac{{50}}{{60}}vong/s\)
\( \to \omega = 2\pi f = 5,23rad/s\)
\(r = l.\sin \alpha \)
\(\begin{array}{l}\tan \alpha = \dfrac{{{F_{ht}}}}{P} = \dfrac{{m{\omega ^2}r}}{{mg}} = \dfrac{{{\omega ^2}.l.\sin \alpha }}{g}\\ \to \dfrac{{\sin \alpha }}{{\cos \alpha }} = \dfrac{{{\omega ^2}.l.\sin \alpha }}{g} \\\to \cos \alpha = \dfrac{g}{{{\omega ^2}.l}} \\= \dfrac{{9,8}}{{{{5,23}^2}.0,5}} = 0,717\\ \to \alpha = {44^0}\end{array}\)
14.6.
Một vệ tinh có khối lượng m = 600 kg đang bay trên quỹ đạo tròn quanh Trái Đất ở độ cao bằng bán kính Trái Đất. Biết Trái Đất có bán kính R = 6 400 km. Lấy g = 9,8 m/s2. Hãy tính:
a) tốc độ dài của vệ tinh.
b) chu kì quay của vệ tinh.
c) lực hấp dẫn tác dụng lên vệ tinh.
Phương pháp giải:
Áp dụng công thức
\({F_{ht}} = m\dfrac{{{v^2}}}{r}\)
\({F_{hd}} = G\dfrac{{m.M}}{{{r^2}}}\)
\(T = \dfrac{{2\pi }}{\omega };\omega = \dfrac{v}{r}\)
Lời giải chi tiết:
a. Lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm
Fhd = Fht
\(\to\displaystyle{{GMm} \over {4{R^2}}} = {{m{v^2}} \over {2R}} \\\to v = \sqrt {{{GM} \over {2R}}} \)
Mặt khác, trên mặt đất ta có:
\(P=mg=\displaystyle{{GMm} \over {{R^2}}} \\\to g = \displaystyle{{GM} \over {{R^2}}} = 9,8m/{s^2}\)
Suy ra:
\(v =\displaystyle \sqrt {{{Rg} \over 2}} = \sqrt {{{{{64.10}^5}.9,8} \over 2}} \\= 5600(m/s) = 5,6 km/s\)
b.
\(T = \displaystyle{{4\pi R} \over v} = {{4.3,{{14.64.10}^5}} \over {5600}} \\= 14354,29s \approx 240ph\)
c.
\({F_{ht}} = \displaystyle{{m{v^2}} \over {2R}} = {{{{600.5600}^2}} \over {2.6400000}} = 1470(N)\)
=> Fhd = 1470 (N)
14.7.
Cho biết chu kì chuyển động của Mặt Trăng quanh Trái Đất là 27,32 ngày và khoảng cách từ Trái Đất đến Mặt Trăng là 3,84.108 m. Hãy tính khối lượng của Trái Đất giả thiết quỹ đạo của Mặt Trăng là tròn.
Phương pháp giải:
\({F_{ht}} = m\dfrac{{{v^2}}}{r}\)
\({F_{hd}} = G\dfrac{{m.M}}{{{r^2}}}\)
\(T = \dfrac{{2\pi }}{\omega };\omega = \dfrac{v}{r}\)
Lời giải chi tiết:
Gọi M và m lần lượt là khối lượng của Trái Đất và của Mặt Trăng, r là bán kính quỹ đạo của Mặt Trăng
Ta có:
\({F_{hd}} = {F_{ht}} \\\to \displaystyle{{GMm} \over {{r^2}}} = m{\omega ^2}r \\ \to M = \displaystyle{{{\omega ^2}{r^3}} \over G}\)
Thay \(\omega = {{2\pi } \over T}\) vào ta được
\(M = \displaystyle{{4{\pi ^2}{r^3}} \over {{T^2}G}} \\= \displaystyle{{4.{{(3,14)}^2}.{{(3,84)}^3}{{.10}^{24}}} \over {{{(27,32)}^2}.{{(864)}^2}{{.10}^4}.6,{{67.10}^{ - 11}}}} \\\approx 6,{00.10^{24}}(kg)\)
14.8.
Một vệ tinh, khối lượng 100 kg, được phóng lên quỹ đạo quanh Trái Đất ở độ cao mà tại đó nó có trọng lượng 920 N. Chu kì của vệ tinh là 5,3.103 s.
a) Tính lực hướng tâm tác dụng lên vệ tinh.
b) Tính khoảng cách từ bề mặt Trái Đất đến vệ tinh.
Phương pháp giải:
Áp dụng công thức
\({F_{ht}} = m{\omega ^2}r\)
\(T = \dfrac{{2\pi }}{\omega }\)
Lời giải chi tiết:
a. Fht = P = 920 N
b. Fht = mω2r = 920 N
\(\to r = \displaystyle{{920.{T^2}} \over {m.4{\pi ^2}}} \\= \displaystyle{{920.{{(5,3)}^2}{{.10}^6}} \over {100.4.{{(3,14)}^2}}} \\= 65,{53.10^5}m = 6553km\)
Do đó, ta có: \(h = r – R = 6553 – 6400 = 153 km\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 14.5, 14.6, 14.7, 14.8 trang 34,35 SBT Vật lí 10 timdapan.com"