Bài 1.42 trang 40 SBT đại số và giải tích 11

Vẽ đồ thị của các hàm số

LG a

\(y=\sin 2x+1\)

Phương pháp giải:

Vẽ đồ thị hàm số \(y=\sin 2x\)

- Hàm số \(y=\sin 2x\) là hàm lẻ tuần hoàn chu kỳ \(\pi\)

- Tìm các điểm đồ thị hàm số \(y=\sin 2x\) đi qua

Vẽ đồ thị hàm số \(y=\sin 2x+1\) bằng cách tịnh tiến đồ thị hàm số \(y=\sin 2x\) song song với trục tung lên phía trên một đơn vị.

Lời giải chi tiết:

Xét hàm số \(y=\sin 2x\)

Với \(x=0\), \(y=0\); \(x=\dfrac{\pi}{4}\), \(y=1\);

\(x=-\dfrac{\pi}{4}\), \(y=-1\); \(x=\dfrac{\pi}{2}\), \(y=0\);

\(x=-\dfrac{\pi}{2}\), \(y=0\)

Khi đó đồ thị hàm số \(y=\sin 2x\) đi qua các điểm là \({\left({0;0}\right)}\); \({\left({\dfrac{\pi}{4}; 1}\right)}\); \({\left({-\dfrac{\pi}{4}; -1}\right)}\); \({\left({\dfrac{\pi}{2}; 0}\right)}\);\({\left({-\dfrac{\pi}{2}; 0}\right)}\)

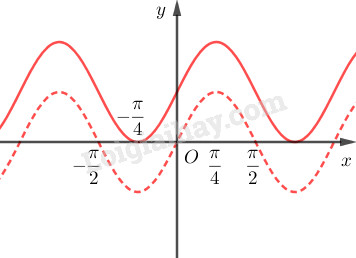
Đồ thị hàm số \(y=\sin 2x+1\) thu được bằng cách tịnh tiến đồ thị hàm số \(y=\sin 2x\) song song với trục tung lên phía trên một đơn vị.

LG b

\(y=\cos {\left({x-\dfrac{\pi}{6}}\right)}\)

Phương pháp giải:

Vẽ đồ thị hàm số \(y=\cos x\)

- Hàm số \(y=\cos x\) là hàm chẵn tuần hoàn chu kỳ \(2\pi\)

- Tìm các điểm đồ thị hàm số \(y=\cos x\) đi qua

Vẽ đồ thị hàm số \(y=\cos {\left({x-\dfrac{\pi}{6}}\right)}\) bằng cách tịnh tiến đồ thị hàm số \(y=\cos x\) song song với trục hoành sang bên phải một đoạn \(\dfrac{\pi}{6}\).

Lời giải chi tiết:

Xét hàm số \(y=\cos x\)

Với \(x=0\), \(y=1\); \(x=\dfrac{\pi}{2}\), \(y=0\);

\(x=-\dfrac{\pi}{2}\), \(y=0\)

Khi đó đồ thị hàm số \(y=\sin 2x\) đi qua các điểm là \({\left({0;0}\right)}\); \({\left({\dfrac{\pi}{2}; 0}\right)}\);\({\left({-\dfrac{\pi}{2}; 0}\right)}\)

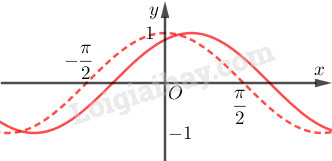
Vẽ đồ thị hàm số \(y=\cos {\left({x-\dfrac{\pi}{6}}\right)}\) bằng cách tịnh tiến đồ thị hàm số \(y=\cos x\) song song với trục hoành sang phải một đoạn bằng \(\dfrac{\pi}{6}\)