Bài 14 trang 62 Vở bài tập toán 9 tập 1

Đề bài

a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị b vừa tìm được.

b) Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A(-1 ; 3). Tìm a. Vẽ đồ thị của hàm số với giá trị a vừa tìm được. 

Lời giải chi tiết

a) Thay \(x = 4;y = 11\) vào hàm số đã cho ta có :

\(11 = 3.4 + b \Leftrightarrow b =  - 1\)

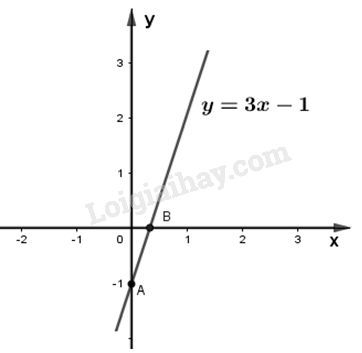
Vậy ta có hàm số \(y = 3x - 1\)

Cho \(x = 0\) thì \(y =  - 1\), ta được \(A\left( {0; - 1} \right)\)

Cho \(y = 0\) thì \(x = \dfrac{1}{3}\) , ta được \(B\left( {\dfrac{1}{3};0} \right)\).

Vẽ đường thẳng đi qua điểm A và B, ta được đồ thị của hàm số \(y = 3x - 1\).

b) Đường thẳng đi qua điểm \(A\left( { - 1;3} \right)\).

Thay giá trị của \(x =  - 1\) và \(y = 3\) vào hàm số đã cho, ta có:

\(3 = a.\left( { - 1} \right) + 5  \Leftrightarrow a = 2\)

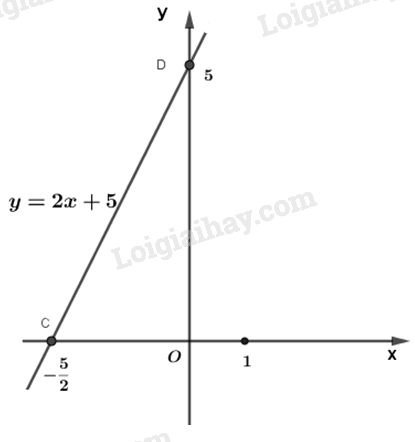
Vậy ta có hàm số \(y = 2x + 5\)

Cho \(x = 0\) thì \(y = 5\), ta được \(D\left( {0;5} \right)\)

Cho \(y = 0\) thì \(x =  - \dfrac{5}{2}\) , ta được \(C\left( { - \dfrac{5}{2};0} \right)\).

Vẽ đường thẳng đi qua hai điểm C và D ta được đồ thị của hàm số \(y = 2x + 5\).