Giải bài 14 trang 25 Chuyên đề học tập Toán 11 Cánh diều
Trong mặt phẳng tọa độ Oxy, cho các điểm A(0; 6), B(6; 3) và điểm M thuộc trục hoành.
Đề bài
Trong mặt phẳng tọa độ Oxy, cho các điểm A(0; 6), B(6; 3) và điểm M thuộc trục hoành.
a) Xác định điểm C đối xứng với B qua trục hoành.
b) Chứng minh rằng MB = MC.
c) Xác định điểm M sao cho tổng MA + MB đạt giá trị nhỏ nhất.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức:
Nếu .\(M' = {Đ_{Ox}}(M)\). thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Lời giải chi tiết
a) Điểm B(6; 3) đối xứng với điểm C qua trục hoành Ox nên C là ảnh của B qua phép đối xứng trục Ox. Do đó C(6; – 3).
b) Vì C là ảnh của điểm B qua phép đối xứng trục Ox nên Ox là đường trung trực của đoạn thẳng BC, do đó điểm M thuộc đường trung trực Ox của BC thì M cách đều B và C, suy ra MB = MC.
c)
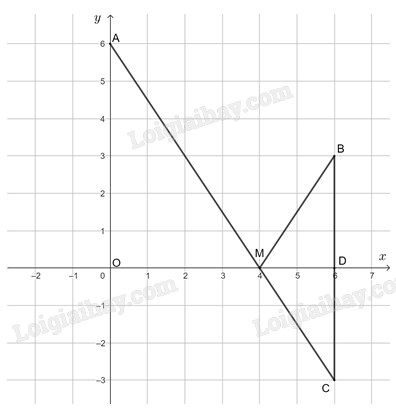
Vì MB = MC nên MA + MB = MA + MC.
Do A và C nằm khác phía nhau đối với trục Ox và M thuộc Ox nên MA + MC ≥ AC.
Dấu “=” xảy ra khi M thuộc AC.
Như vậy M là giao điểm của AC và Ox thì tổng MA + MB đạt giá trị nhỏ nhất bằng AC.
Ta có: \(OA = \sqrt {{6^2} + {0^2}} = 6,\,BC = \sqrt {{{\left( {6 - 6} \right)}^2} + {{\left( { - 3 - 3} \right)}^2}} = 6\).
Gọi D là giao điểm của BC và Ox, khi đó \(CD = \frac{1}{2}BC = 3\) và OA // CD.
Suy ra \(\frac{{OM}}{{MD}} = \frac{{OA}}{{CD}} = \frac{6}{3} = 2\). Suy ra \(OM{\rm{ }} = {\rm{ }}2MD\;\) nên \(OM = \frac{2}{3}OD = \frac{2}{3}.6 = 4\).
Do đó, M(4; 0).
Vậy M(4; 0) thì tổng MA + MB đạt giá trị nhỏ nhất.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 14 trang 25 Chuyên đề học tập Toán 11 Cánh diều timdapan.com"







