Bài 14 trang 103 Vở bài tập toán 8 tập 1
Giải bài 14 trang 103 VBT toán 8 tập 1. Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường xy.
Đề bài
Hai điểm \(A\) và \(B\) thuộc cùng một nửa mặt phẳng có bờ là đường \(xy.\) Khoảng cách từ điểm \(A\) đến \(xy\) bằng \(12\,cm\), khoảng cách từ điểm \(B\) đến \(xy\) bằng \(20\,cm.\) Tính khoảng cách từ trung điểm \(C\) của \(AB\) đến \(xy.\)
Phương pháp giải - Xem chi tiết
Áp dụng:
- Hình thang là tứ giác có hai cạnh đối song song.
- Đường trung bình hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
- Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
- Định lí: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Lời giải chi tiết
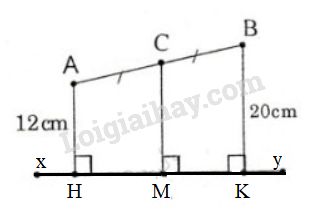
Kẻ \(AH, CM, BK\) vuông góc \(xy\) (\(H, M, K\) là chân đường vuông góc).
\( \Rightarrow AH//CM//BK\) (cùng vuông góc với đường thẳng \(xy\))
Hình thang \(ABKH\) có \(AC = CB\) và \(CM // AH // BK\) (cùng vuông góc \(xy\))
nên \(MH = MK\)
và \( CM\) là đường trung bình của hình thang \(ABKH\)
Do đó \(CM = \dfrac{{AH + BK}}{2} = \dfrac{{12 + 20}}{2} \)\(\,= \dfrac{{32}}{2}\)\(= 16\left( {cm} \right)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 14 trang 103 Vở bài tập toán 8 tập 1 timdapan.com"







