Bài 1.25 trang 19 SBT hình học 12
Giải bài 1.25 trang 19 sách bài tập hình học 12. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông ở B, AB = BC = AA’. Hãy chia lăng trụ đó thành ba tứ diện bằng nhau.
Đề bài
Cho hình lăng trụ đứng \(ABC.A’B’C’\) có đáy là tam giác vuông ở \(B\), \(AB = BC = AA’\). Hãy chia lăng trụ đó thành ba tứ diện bằng nhau.
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa đa diện bằng nhau: Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
Lời giải chi tiết
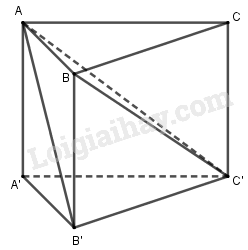
Chia lăng trụ đã cho thành ba tứ diện: \(ABCC’ , ABB’C’\) và \(AA’B’C’\).
+) Phép đối xứng qua mặt phẳng \( (ABC’) \) biến tứ diện \(ABCC’\) thành tứ diện \(ABB’C’\).
+) Phép đối xứng qua mặt phẳng \( (AB’C’) \) biến tứ diện \(ABB’C’\) thành tứ diện \(AA’B’C’\).
Vậy ba tứ diện đó bằng nhau.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.25 trang 19 SBT hình học 12 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.25 trang 19 SBT hình học 12 timdapan.com"







