Bài 1.1 trang 9 SBT hình học 12
Giải bài 1.1 trang 9 sách bài tập hình học 12. Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai tứ diện A’ABD và CC’D’B’ bằng nhau.
Đề bài
Cho hình hộp \(ABCD.A’B’C’D’\) . Chứng minh rằng hai tứ diện \(A’ABD\) và \(CC’D’B’\) bằng nhau.
Phương pháp giải - Xem chi tiết
Dùng phép đối xứng qua tâm của hình hộp.
Lời giải chi tiết
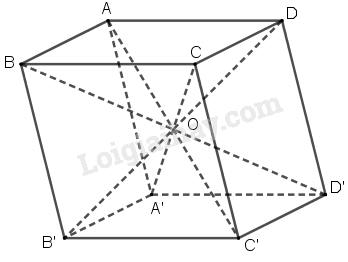
Gọi \(O\) là tâm hình hộp \(ABCD.A’B’C’D’\).
Ta có \(O\) là trung điểm của \(A’C, AC’, BD’, DB’\). Phép đối xứng tâm \(O\) biến các điểm \(A’, A, B, D\) lần lượt thành các điểm \(C, C’, D’, B’\). Do đó hai tứ diện \(A’ABD\) và \(CC’D’B’\) bằng nhau vì có phép dời hình là phép đối xứng tâm \(O\) biến tứ diện này thành tứ diện kia.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.1 trang 9 SBT hình học 12 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.1 trang 9 SBT hình học 12 timdapan.com"







