Bài 1.1, 1.2, 1.3, 1.4 phần bài tập bổ sung trang 100, 101 SBT toán 7 tập 1

Bài 1.1

Mỗi câu sau là đúng hay sai ?

a) Có những cặp góc bằng nhau nhưng không phải là hai góc đối đỉnh.

b) Hai góc bằng nhau và một đường thẳng chứa tia của góc này có chứa tia của góc kia là hai góc đối đỉnh.

c) Hai góc bằng nhau và một tia của góc này là tia đối của góc kia là hai góc đối đỉnh.

d) Hai góc bằng nhau và có chung đỉnh là hai góc đối đỉnh.

e) Góc tạo bởi hai tia đối của một góc và góc đã cho là hai góc đối đỉnh.

f) Hai đường thẳng cắt nhau tạo thành 4 góc, đôi một đối đỉnh.

g) Hai góc đối đỉnh thì hai góc đó phải là góc nhọn

Phương pháp:

- Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Tính chất: Hai góc đối đỉnh thì bằng nhau.

- Tổng hai góc kề bù bằng \(180^o\). 

Lời giải:

a) Đúng, ví dụ như hình vẽ. 

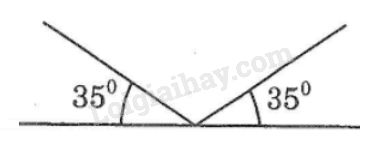
b) Sai (hình vẽ câu a)

c) Sai (hình vẽ câu a)

d) Sai (hình vẽ câu a)

e) Đúng (theo định nghĩa hai góc đối đỉnh)

f) Sai, ví dụ:

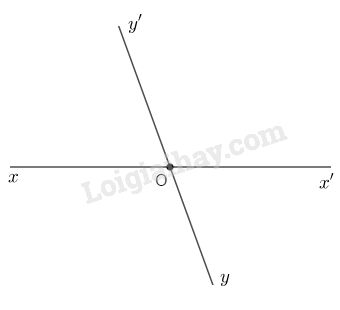
\(\widehat {xOy}\) và \(\widehat {yOx'}\) không đối đỉnh.

g) Sai, ví dụ hình vẽ câu f) ta có:

\(\widehat {xOy}\) và \(\widehat {x'Oy'}\) đối đỉnh nhưng hai góc này là hai góc tù.

Bài 1.2

Ba đường thẳng phân biệt \(xy, mn, zt\) cùng đi qua điểm \(O\) và tạo thành các góc \(\widehat {zOx} = {38^o},\,\widehat {tOm} = {71^o}\) (h.bs 1).

a) Đọc tên các cặp góc đối đỉnh có trong hình đó.

b) Cho biết số đo của các góc còn lại có trong hình đó.

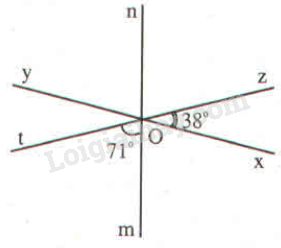
Phương pháp:

- Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Tính chất: Hai góc đối đỉnh thì bằng nhau.

- Tổng hai góc kề bù bằng \(180^o\). 

Lời giải:

a) Các cặp góc đối đỉnh là: \(\widehat {xOz}\) và \(\widehat {tOy}\); \(\widehat {xOn}\) và \(\widehat {mOy}\); \(\widehat {zOn}\) và \(\widehat {tOm}\); \(\widehat {xOm}\) và \(\widehat {nOy}\); \(\widehat {xOt}\) và \(\widehat {zOy}\), \(\widehat {mOz}\) và \(\widehat {tOn}\); các góc bẹt như \(tOz, yOx, nOm\) có góc đối đỉnh là chính nó.

b) Từ các cặp góc đối đỉnh suy ra ngay:

\(\widehat {zOx} = \widehat {tOy} = 38^\circ ,\widehat {tOm} = \widehat {zOn} = 71^\circ \)

\(\widehat {tOz}\) là góc bẹt nên ta có:

\(\widehat {xOm} = 180^\circ  - \left( {71^\circ  + 38^\circ } \right) = 71^\circ \)

Từ đó, \(\widehat {xOm} = \widehat {yOn} = 71^\circ \).

Các góc bẹt như \(tOz, yOx, nOm\) đều có số đo là \(180^\circ \)

Bài 1.3

a) Cho góc mOn. Vẽ góc nOt kề bù với góc mOn. Vẽ góc mOz kề bù với góc mOn. Khi đó mOn và tOz có phải là hai góc đối đỉnh không?

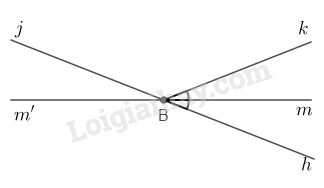
b) Cho góc hBk. Vẽ Bm là tia phân giác của góc hBk. Vẽ Bm' là tia đối của tia Bm. Vẽ góc kBj kề bù với góc hBk. Khi đó các góc m'Bj và hBm có phải là hai góc đối đỉnh không?

c) Cho góc xOy. Vẽ góc yOz kề bù với xOy. Vẽ góc xOt kề bù với góc xOy. Vẽ On là tia phân giác của góc zOy. Vẽ Om là tia phân giác của góc tOx. Khi đó zOn và xOm có phải là hai góc đối đỉnh không?

Phương pháp:

- Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Tính chất: Hai góc đối đỉnh thì bằng nhau.

- Hai góc kề bù là hai góc có một cạnh chung và hai cạnh còn lại là hai tia đối nhau, tổng số đo hai góc kề bù bằng \(180^o\). 

Lời giải:

a) Vì góc nOt kề bù với góc mOn nên Ot là tia đối của tia Om. Tương tự, góc mOz kề bù với góc mOn nên Oz là tia đối của tia On. Từ đó, mOn và tOz là hai góc đối đỉnh.

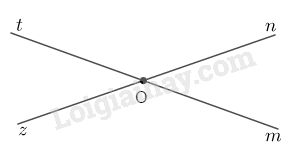
b) Vì góc kBj kề bù với góc hBk nên Bj là tia đối của tia Bh. Từ đó, m’Bj và hBm là hai góc đối đỉnh.

c)

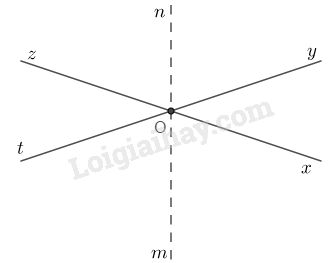
Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, zOy và tOx là hai góc đối đỉnh, tức là \(\widehat {zOy} = \widehat {tOx}\).

Vì On, Om lần lượt là tia phân giác của \(\widehat {zOy} \) và \( \widehat {tOx}\) nên \(\widehat {zOn} = \widehat {nOy} = \widehat {xOm} = \widehat {mOt}\).

Lại vì \(\widehat {zOn} + \widehat {nOx} = 180^\circ \) (hai góc kề bù)

Nên \(\widehat {mOx} + \widehat {nOx} = 180^\circ \).

Suy ra Om và On là hai tia đối nhau.

Từ đó, \(\widehat {zOn}\) và \(\widehat {mOx}\) là hai góc đối đỉnh.

Bài 1.4

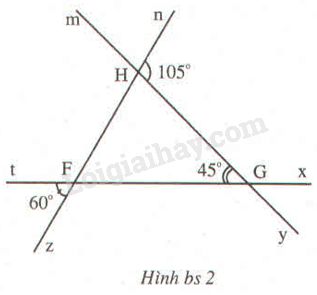
Căn cứ số đo của các góc đã cho hãy tìm số đo của các góc còn lại có trong hình bs2.

Phương pháp:

- Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Tính chất: Hai góc đối đỉnh thì bằng nhau.

- Tổng số đo hai góc kề bù bằng \(180^o\). 

Lời giải:

\(\widehat {FGH}\) và \(\widehat {HGx}\) là hai góc kề bù nên:

\(\widehat {HGx} = {180^o} - \widehat {FGH} = {180^o} - {45^o}\)\(\, = {135^o}\)

\(\widehat {tFz}\) và \(\widehat {tFH}\) là hai góc kề bù nên:

\(\widehat {tFH} = {180^o} - \widehat {tFz} = {180^o} - {60^o} \)\(\,= {120^o}\)

\(\widehat {nHG}\) và \(\widehat {FHG}\) là hai góc kề bù nên:

\(\widehat {FHG} = {180^o} - \widehat {nHG} = {180^o} - {105^o} \)\(\,= {75^o}\)

Ta có các cặp góc đối đỉnh bằng nhau là:

\(\begin{array}{l}
\widehat {HFG} = \widehat {zFt} = {60^o};\\\widehat {xGy} = \widehat {HGF} = {45^o};\\
\widehat {mHF} = \widehat {nHG} = {105^o};\\\widehat {HFt} = \widehat {zFG} = {120^o};\\
\widehat {yGF} = \widehat {xGH} = {135^o};\\\widehat {GHF} = \widehat {nHm} = {75^o}.
\end{array}\)