Đề thi vào lớp 6 môn Toán trường THCS Nam Từ Liêm năm 2023

Đề bài

ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS NAM TỪ LIÊM

NĂM HỌC 2023 – 2024

Thời gian làm bài: 50 phút

PHẦN 1. TRẮC NGHIỆM

Câu 1. Trung bình cộng của dãy số sau là bao nhiêu?

15 ; 45 ; 75

Câu 2. Số $\overline {2a1a} $ chia hết cho 9. Tìm a.

Câu 3. Hoa mua một quyển sách được giảm 10% thì hết 72 000 đồng. Hỏi giá gốc của quyển sách là bao nhiêu?

Câu 4. Năm nay, mẹ hơn con 25 tuổi. Hai năm nữa, tuổi con bằng $\frac{1}{6}$ tuổi mẹ. Tính tuổi con hiện nay.

Câu 5. Một bể nước hình chữ nhật có chiều dài 50m, chiều rộng 30m. Thể tích nước trong bể là 2 100m³. Tính chiều cao mực nước trong bể.

Câu 6. Tổng số sách trong 2 ngăn là 48 quyển. Sau khi chuyển 3 quyển từ ngăn 1 sang ngăn 2 thì số sách ngăn 1 bằng $\frac{3}{5}$ số sách ngăn 2. Tìm số sách ngăn 2.

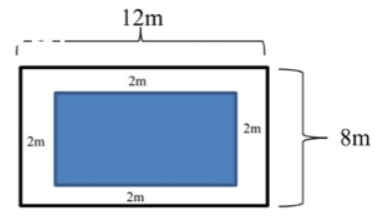
Câu 7. Tính diện tích hình tô đậm.

Câu 8. An viết tất cả các số có 3 chữ số mà có đầy đủ các chữ số 1, 2, 3. Hỏi có bao nhiêu số lớn hơn 222 mà An có thể viết được.

Câu 9. Tìm số bé nhất có 3 chữ số, khi xóa chữ số hàng trăm của số đó, ta được số mới bằng $\frac{1}{9}$ số cũ.

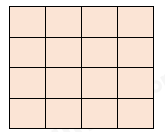
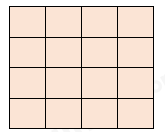
Câu 10. Hình dưới có bao nhiêu hình vuông?

PHẦN 2. TỰ LUẬN

Câu 1

a) Tính nhanh: 2,4 x 150 + 8,6 x 240 – 24

b) Tìm x biết: $\left( {\frac{3}{4} - \frac{1}{4} \times x} \right) \times \frac{{33}}{{11}} = \frac{{15}}{8}$

c) Quãng đường AB dài 75 km. An xuất phát từ A và Bình xuất phát từ B thì hai người gặp nhau sau $2\frac{7}{9}$ giờ. Nếu Bình tăng vận tốc thêm 3 km mỗi giờ thì hai bạn sẽ gặp nhau ở chính giữa quãng đường. Tính vận tốc của mỗi người.

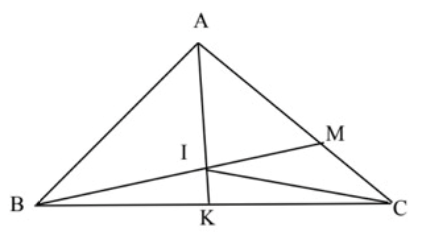
Câu 2. Cho tam giác ABC có diện tích bằng 90 cm². Trên cạnh AC lấy điểm M sao cho AM = 2 MC. Lấy I là trung điểm của BM. Kéo dài AI cắt BC tại K.

a) Tính diện tích tam giác BMC.

b) Tính tỉ số diện tích hai tam giác ABI và BIC

c) So sánh $\frac{{BK}}{{KC}}$

---

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

PHẦN 1. TRẮC NGHIỆM

Câu 1. Trung bình cộng của dãy số sau là bao nhiêu?

15 ; 45 ; 75

Cách giải: Trung bình cộng của ba số đó là (15 + 45 + 75) : 3 = 45

Câu 2. Số $\overline {2a1a} $ chia hết cho 9. Tìm a.

Cách giải: $\overline {2a1a} $ chia hết cho 9 $ \Rightarrow $ (2 + a + 1 + a) chia hết cho 9

$ \Rightarrow $(3 + a x 2) chia hết cho 9 $ \Rightarrow $ a x 2 = 6 $ \Rightarrow $ a = 3

Câu 3. Hoa mua một quyển sách được giảm 10% thì hết 72 000 đồng. Hỏi giá gốc của quyển sách là bao nhiêu?

Cách giải:

72 000 đồng ứng với số phần trăm giá gốc là:

             100% - 10% = 90%

Giá gốc quyển sách là:

         72 000 : 90% = 80 000 (đồng)

                        Đáp số: 80 000 đồng

Câu 4. Năm nay, mẹ hơn con 25 tuổi. Hai năm nữa, tuổi con bằng $\frac{1}{6}$ tuổi mẹ. Tính tuổi con hiện nay.

Cách giải:

Vì hiệu số tuổi của hai mẹ con không thay đổi nên mẹ luôn hơn con 25 tuổi.

Tuổi con 2 năm nữa là:

        25 : 96 – 1) = 5 (tuổi)

Tuổi con hiện nay là:

        5 – 2 = 3 (tuổi)

               Đáp số: 3 tuổi

Câu 5. Một bể nước hình chữ nhật có chiều dài 50m, chiều rộng 30m. Thể tích nước trong bể là 2 100m³. Tính chiều cao mực nước trong bể.

Cách giải:

Chiều cao mực nước trong bể là:

      2 100 : 50 : 30 = 1,4 (m)

                 Đáp số: 1,4 m

Câu 6. Tổng số sách trong 2 ngăn là 48 quyển. Sau khi chuyển 3 quyển từ ngăn 1 sang ngăn 2 thì số sách ngăn 1 bằng $\frac{3}{5}$ số sách ngăn 2. Tìm số sách ngăn 2.

Cách giải:

Sau khi chuyển 3 quyển từ ngăn 1 sang ngăn 2 thì tổng số sách hai ngăn không đổi.

Số sách ngăn 2 lúc sau là:

          48 : (3 + 5) x 5= 30 (quyển)

Số sách ngăn 2 lúc đầu là:

          30 – 3 = 27 (quyển)

                   Đáp số: 27 quyển

Câu 7. Tính diện tích hình tô đậm.

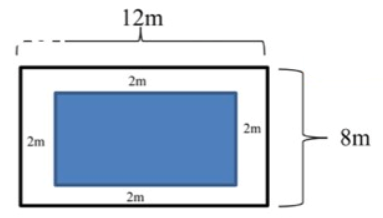
Cách giải:

Chia hình đã cho thành các hình chữ nhật nhỏ như sau:

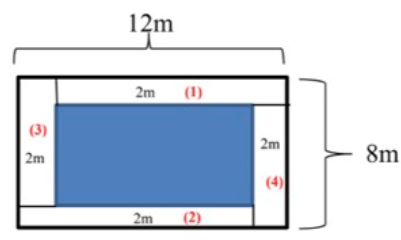
Diện tích hình (1) = diện tích hình (2) và bằng:

(12 – 2) x 2 = 20 (m²)

Diện tích hình (3) = diện tích hình (4) và bằng:

(8 – 2) x 2 = 12 (m²)

Diện tích hình chữ nhật lớn bên ngoài là:

12 x 8 = 96 (m²)

Diện tích hình tô đậm là:

96 – 12 x 2 – 20 x 2 = 32 (m²)

Đáp số: 32 m²

Câu 8. An viết tất cả các số có 3 chữ số mà có đầy đủ các chữ số 1, 2, 3. Hỏi có bao nhiêu số lớn hơn 222 mà An có thể viết được.

Cách giải:

Các số có ba chữ số mà có đầy đủ các chữ số 1, 2, 3 và lớn hơn 222 là 321, 312, 231

Vậy có thể viết được 3 số thoải mãn đề bài.

Câu 9. Tìm số bé nhất có 3 chữ số, khi xóa chữ số hàng trăm của số đó, ta được số mới bằng $\frac{1}{9}$ số cũ.

Cách giải:

Gọi số cần tìm là $\overline {abc} $ (a khác 0, a, b, c < 10)

Ta có: $\overline {abc}  = \overline {bc}  \times 9$

$a \times 100 + \overline {bc}  = \overline {bc}  \times 9$

$a \times 100 = \overline {bc}  \times 8$

$a \times 25 = \overline {bc}  \times 2$

Vì a x 25 chia hết cho 25 $ \Rightarrow \overline {bc}  \times 2$chia hết cho 25 $ \Rightarrow \overline {bc} $ = 25, 50, 75, 100, …

Số cần tìm nhỏ nhất khi a, $\overline {bc} $ lần lượt nhỏ nhất $ \Rightarrow \overline {bc}  = 25$

$ \Rightarrow $ 25 x 2 : 25 = 2

Vậy số bé nhất cần tìm là 225.

Câu 10. Hình dưới có bao nhiêu hình vuông?

Cách giải:

Số hình vuông được tạo từ một ô vuông là 16 (hình)

Số hình vuông được tạo từ 4 ô vuông là 9 (hình)

Số hình vuông được tạo từ 9 ô vuông là 4 (hình)

Số hình vuông được tại từ 16 ô vuông là 1 (hình)

$ \Rightarrow $ Có tất cả 16 + 9 + 4 + 1 = 30 (hình)

PHẦN 2. TỰ LUẬN

Câu 1

a) Tính nhanh: 2,4 x 150 + 8,6 x 240 – 24

b) Tìm x biết: $\left( {\frac{3}{4} - \frac{1}{4} \times x} \right) \times \frac{{33}}{{11}} = \frac{{15}}{8}$

c) Quãng đường AB dài 75 km. An xuất phát từ A và Bình xuất phát từ B thì hai người gặp nhau sau $2\frac{7}{9}$ giờ. Nếu Bình tăng vận tốc thêm 3 km mỗi giờ thì hai bạn sẽ gặp nhau ở chính giữa quãng đường. Tính vận tốc của mỗi người.

Cách giải:

a) 2,4 x 150 + 8,6 x 240 – 24

= 24 x 15 + 86 x 24 – 24

= 24 x (15 + 86 – 1)

= 24 x 100

= 2 400

b) $\left( {\frac{3}{4} - \frac{1}{4} \times x} \right) \times \frac{{33}}{{11}} = \frac{{15}}{8}$

    $\frac{3}{4} - \frac{1}{4} \times x = \frac{{15}}{8}:\frac{{33}}{{11}}$

    $\frac{3}{4} - \frac{1}{4} \times x = \frac{5}{8}$

$\frac{1}{4} \times x = \frac{3}{4} - \frac{5}{8}$

$\frac{1}{4} \times x = \frac{1}{8}$

$x = \frac{1}{8}:\frac{1}{4}$

$x = \frac{1}{2}$

c) Đổi $2\frac{7}{9}$ giờ = $\frac{{25}}{9}$ giờ

Tổng vận tốc của an và Bình là:

          $75:\frac{{25}}{9} = 27$(km/giờ)

Nếu Bình tăng vận tốc thêm 3 km mỗi giờ thì hai bạn sẽ gặp nhau ở chính giữa quãng đường nên vận tốc của An hơn vận tốc của Bình là 3 km/giờ.

Vận tốc của Bình là:

         (27 – 3) : 2 = 12 (km/giờ)

Vận tốc của An là:

         12 + 3 = 15 (km/giờ)

               Đáp số: An: 15 km/giờ

                            Bình: 12km/giờ

Câu 2. Cho tam giác ABC có diện tích bằng 90 cm². Trên cạnh AC lấy điểm M sao cho AM = 2 MC. Lấy I là trung điểm của BM. Kéo dài AI cắt BC tại K.

a) Tính diện tích tam giác BMC.

b) Tính tỉ số diện tích hai tam giác ABI và BIC

c) So sánh $\frac{{BK}}{{KC}}$

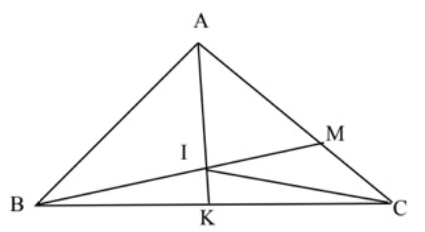
Cách giải:

a) S_BMC = $\frac{1}{3}$S_ABC (Chung đường cao hạ từ B và đáy MC = $\frac{1}{3}$ AC)

$ \Rightarrow $S_BMC = $90 \times \frac{1}{3} = 30$ (cm²)

b) Nối IC ta có:

S_ABM = 2 x S_BMC (Chung chiều cao hạ từ B và đấy AM = 2 x MC)

$ \Rightarrow $Chiều cao hạ từ A xuống BM gấp 2 lần chiều cao hạ từ C xuống đáy BM

$ \Rightarrow $S_ABI = 2 x S_BIC (Chung đáy BI và chiều cao hạ từ A xuống BM gấp 2 lần chiều cao hạ từ C xuống đáy BM)

c) S_ABI = S_AIM (Chung chiều cao hạ từ A và đáy BI = IM)

Mà S_AIM = $\frac{2}{3}$ S_AIC (Chung đường cao hạ từ I và đáy AM = $\frac{2}{3}$ AC)

$ \Rightarrow $S_ABI = S_AIC

$ \Rightarrow $ Đường cao hạ từ B xuống AI = $\frac{2}{3}$ đường cao từ C xuống AI

$ \Rightarrow $S_BAK = $\frac{2}{3}$S_CAK (Chung đáy AK và đường cao hạ từ B xuống AK = $\frac{2}{3}$ đường cao từ C xuống AK)

$ \Rightarrow $BK = $\frac{2}{3}$ CK