Đề thi vào lớp 6 môn Toán trường Nguyễn Tất Thành năm 2023
Một bể bóng trong khu vui chơi có 360 quả bóng bao gồm bóng màu vàng ... Một bể kính dạng hình hộp chữ nhật có chiều dài 1 m, chiều rộng 5 dm, ....
Đề thi
ĐỀ TUYỂN SINH LỚP 6 TRƯỜNG THCS VÀ THPT NGUYỄN TẤT THÀNH NĂM HỌC 2023 - 2024
Môn: TOÁN
Thời gian làm bài: 45 phút
Mã đề 601
I. TRẮC NGHIỆM (Khoanh vào chữ cái trước đáp án đúng từ Câu 1 đến Câu 4)
Câu 1. Kết quả phép tính 2,75 x 0,99 + 2,75 : 100 bằng:
A. 0,275
B. 2,75
C. 27,5
D. 275
Câu 2. Một bể bóng trong khu vui chơi có 360 quả bóng bao gồm bóng màu vàng và bóng màu xanh, $\frac{3}{5}$ số quả bóng trong bể có màu xanh. Số quả bóng màu vàng trong bể đó là:
A. 225 quả
B. 135 quả
C. 144 quả
D. 216 quả
Câu 3. Một bể kính dạng hình hộp chữ nhật có chiều dài 1 m, chiều rộng 5 dm, chiều cao 6 dm (bỏ qua độ dày của các tấm kính). Hiện mực nước trong bể cao bằng $\frac{2}{3}$ chiều cao của bể. Lượng nước đang có trong bể kính đó là:
A. 200 dm3
B. 300 dm3
C. 200 m3
D. 30 dm3
Câu 4. Biểu đồ cột dưới đây cho biết số lượng học sinh khối 6 tham gia câu lạc bộ nghệ thuật trong hè 2023 của trường THCS và THPT Nguyễn Tất Thành.
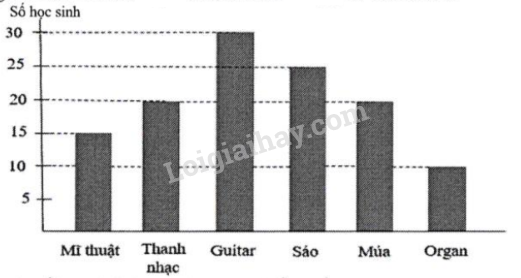
Tỉ số phần trăm của số học sinh học Guitar so với tổng số học sinh tham gia câu lạc bộ nghệ thuật hè 2023 của trường THCS và THPT Nguyễn Tất Thành là:
A. 25 %
B. 30%
C. 12.5%
D. 75%
II. TRẢ LỜI NGẮN (Viết đáp số của bài toán vào ô trống từ Câu 5 đến Câu 8)
|
Câu 5. Trung bình cộng của 3 số bằng 15,3. Trung bình cộng của số thứ nhất và số thứ hai bằng 12,1. Tìm số thứ ba. |
|
|
Câu 6. Nhân dịp ngày Quốc tế Thiếu nhi mùng 1 tháng 6, một cửa hàng quần áo trẻ em giảm giá 15% tất cả các sản phẩm so với giá niêm yết. Mẹ bạn Mai mua một bộ váy tại hàng đó và đã trả 212 500 đồng. Hỏi bộ váy đó có giá niêm yết là bao nhiêu tiền? |
|
|
Câu 7. Tìm số tự nhiên lớn nhất có dạng $\overline {a1024b} $. Biết số đó có sáu chữ số và chia hết cho 45. |
|
|
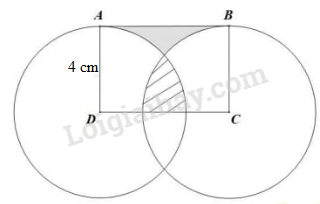
Câu 8. Hình chữ nhật ABCD có cạnh AD bằng 4 cm. Hình tròn tâm D, bán kính DA và hình tròn tâm C , bán kính CB có vị trí như hình bên. Hãy tính độ dài cạnh CD biết diện tích phần tô đậm bằng diện tích phần gạch chéo.
|
III. TỰ LUẬN (Trình bày chi tiết lời giải Câu 9 và Câu 10)
Câu 9. Hai bạn An và Bình cùng đạp xe từ trường đến sân vận động để tham gia thi đấu thể thao. Thời gian An đạp xe từ trường đến sân vận động bằng $\frac{5}{4}$ thời gian Bình đạp xe từ trường đến sân vận động. Biết trong 6 phút bạn An đạp xe được quãng đường dài 1,2 km.
1. Tính vận tốc của bạn An.
2. Tính độ dài quãng đường từ trường đến sân vận động biết rằng nếu trên cùng quãng đường đó và cùng một lúc An xuất phát từ trường còn Bình xuất phát từ sân vận động thì sau 12 phút 2 bạn sẽ gặp nhau.
(Biết vận tốc của 2 bạn không thay đổi)
Câu 10. Cho hình chữ nhật ABCD. Trên AB lấy điểm E sao cho AB = AE x 3, DB cắt EC tại G.
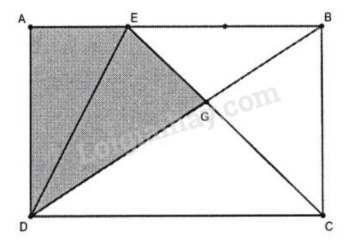
Biết diện tích hình chữ nhật ABCD là 144 cm2, tính:
1. Diện tích tam giác AED.
2. Diện tích tứ giác AEGD.
Đáp án
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Kết quả phép tính 2,75 x 0,99 + 2,75 : 100 bằng:
A. 0,275
B. 2,75
C. 27,5
D. 275
Lời giải
2,75 x 0,99 + 2,75 : 100 = 2,75 x 0,99 + 2,75 x 0,01
= 2,75 x (0,99 + 0,01)
= 2,75 x 1 = 2,75
Chọn B
Câu 2. Một bể bóng trong khu vui chơi có 360 quả bóng gồm bóng màu vàng và bóng màu xanh, $\frac{3}{5}$ số quả bóng trong bể có màu xanh. Số quả bóng màu vàng trong bể đó là:
A. 225 quả
B. 135 quả
C. 144 quả
D. 216 quả
Lời giải
Số bóng xanh trong bể là $\frac{3}{5} \times 360 = 216$ (quả)
Số quả bóng vàng trong bể là 360 – 216 = 144 (quả)
Chọn C
Câu 3. Một bể kính dạng hình hộp chữ nhật có chiều dài 1 m, chiều rộng 5 dm, chiều cao 6 dm (bỏ qua độ dày của các tấm kính). Hiện mực nước trong bể cao bằng $\frac{2}{3}$ chiều cao của bể. Lượng nước đang có trong bể kính đó là:
A. 200 dm3
B. 300 dm3
C. 200 m3
D. 30 dm3
Lời giải
Đổi: 1 m = 10 dm
Chiều cao mực nước trong bể là $\frac{2}{3} \times 6 = 4$ (dm)
Thể tích nước có trong bể kính đó là: 10 x 5 x 4 = 200 (dm3)
Chọn A
Câu 4. Biểu đồ cột dưới đây cho biết số lượng học sinh khối 6 tham gia câu lạc bộ nghệ thuật trong hè 2023 của trường THCS và THPT Nguyễn Tất Thành.
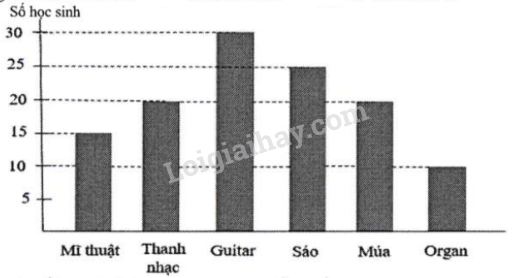
Tỉ số phần trăm của số học sinh học Guitar so với tổng số học sinh tham gia câu lạc bộ nghệ thuật hè 2023 của trường THCS và THPT Nguyễn Tất Thành là:
A. 25 %
B. 30%
C. 12,5%
D. 75%
Lời giải
Tổng số học sinh tham gia câu lạc bộ nghệ thuật hè là:
15 + 20 + 30 + 25 + 20 + 10 = 120 (học sinh)
Tỉ số phần trăm của số học sinh học Guitar so với tổng số học sinh tham gia câu lạc bộ nghệ thuật hè 2023 của trường THCS và THPT Nguyễn Tất Thành là:
30 : 120 x 100% = 25 %
Chọn A
Câu 5. Trung bình cộng của 3 số bằng 15,3. Trung bình cộng của số thứ nhất và số thứ hai bằng 12,1. Tìm số thứ ba.
Lời giải
Tổng của ba số là 15,3 x 3 = 45,9
Tổng của số thứ nhất và số thứ hai là 12,1 x 2 = 24,2
Số thứ ba là 45,9 - 24,2 = 21,7
Đáp số: 21,7
Câu 6. Nhân dịp ngày Quốc tế Thiếu nhi mùng 1 tháng 6, một cửa hàng quần áo trẻ em giảm giá 15% tất cả các sản phẩm so với giá niêm yết. Mẹ bạn Mai mua một bộ váy tại cửa hàng đó và đã trả 212 500 đồng. Hỏi bộ váy đó có giá niêm yết là bao nhiêu tiền?
Lời giải
Giá bán của chiếc váy chiếm 100% - 15% = 85% (giá niêm yết)
Giá niêm yết của chiếc váy đó là 212 500 : 85 x 100 = 250 000 (đồng)
Đáp số: 250 000 đồng
Câu 7. Tìm số tự nhiên lớn nhất có dạng $\overline {a1024b} $. Biết số đó có sáu chữ số và chia hết cho 45.
Lời giải
Để số $\overline {a1024b} $ chia hết cho 45 thì $\overline {a1024b} $ chia hết cho 5 và 9.
Để số $\overline {a1024b} $ chia hết cho 5 thì b = 0 hoặc b = 5
Trường hợp 1: b = 0. Ta có số $\overline {a10240} $ chia hết cho 9
Suy ra a + 7 chia hết cho 9. Do đó a = 2. Ta có số 210240
Trường hợp 1: b = 5. Ta có số $\overline {a10245} $ chia hết cho 9
Suy ra a + 12 chia hết cho 9. Do đó a = 6. Ta có số 610245
Vậy số cần tìm là 610245
Đáp số: 610245
Câu 8. Hình chữ nhật ABCD có cạnh AD bằng 4 cm. Hình tròn tâm D, bán kính DA và hình tròn tâm C , bán kính CB có vị trí như hình bên. Hãy tính độ dài cạnh CD biết diện tích phần tô đậm bằng diện tích phần gạch chéo.
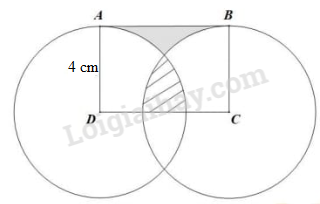
Lời giải
Diện tích $\frac{1}{4}$ hình tròn tâm D, bán kính DA là $\frac{1}{4} \times 4 \times 4 \times 3,14 = 12,56$ (cm2)
Diện tích $\frac{1}{4}$ hình tròn tâm C, bán kính CB là $\frac{1}{4} \times 4 \times 4 \times 3,14 = 12,56$ (cm2)
Vì diện tích phần tô đậm bằng diện tích phần gạch chéo nên diện tích hình chữ nhật ABCD là:
12,56 + 12,56 = 25,12 (cm2)
Độ dài cạnh CD là 25,12 : 4 = 6,28 (cm)
Đáp số: 6,28 cm
Câu 9. Hai bạn An và Bình cùng đạp xe từ trường đến sân vận động để tham gia thi đấu thể thao. Thời gian An đạp xe từ trường đến sân vận động bằng $\frac{5}{4}$ thời gian Bình đạp xe từ trường đến sân vận động. Biết trong 6 phút bạn An đạp xe được quãng đường dài 1,2 km.
1. Tính vận tốc của bạn An.
2. Tính độ dài quãng đường từ trường đến sân vận động biết rằng nếu trên cùng quãng đường đó và cùng một lúc An xuất phát từ trường còn Bình xuất phát từ sân vận động thì sau 12 phút 2 bạn sẽ gặp nhau.
(Biết vận tốc của 2 bạn không thay đổi)
Lời giải
1. Đổi: 6 phút = $\frac{1}{{10}}$ giờ
Vận tốc của An là: $1,2:\frac{1}{{10}} = 12$ (km/giờ)
2. Trên cùng một quãng đường thì thời gian và vận tốc tỉ lệ nghịch với nhau.
t An : t Bình = v Bình : v An = $\frac{5}{4}$
Vận tốc của Bình là $12 \times \frac{5}{4} = 15$ (km/giờ)
Tổng vận tốc của An và Bình là 12 + 15 = 27 (km/giờ)
Đổi: 12 phút = $\frac{1}{5}$ giờ
Quãng đường từ trường đến sân vận động là $27 \times \frac{1}{5} = 5,4$ (km)
Đáp số: 1) 12 km/giờ
2) 5,4 km
Câu 10. Cho hình chữ nhật ABCD. Trên AB lấy điểm E sao cho AB = AE x 3, DB cắt EC tại G.
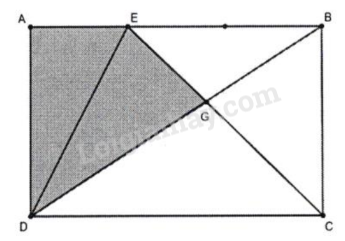
Biết diện tích hình chữ nhật ABCD là 144 cm2, tính:
1. Diện tích tam giác AED.
2. Diện tích tứ giác AEGD.
Lời giải
1. ${S_{ABD}} = {S_{BDC}} = \frac{1}{2} \times {S_{ABCD}} = 144:2 = 72$(cm2)
SAED = $\frac{1}{3}$ SABD (Hai tam giác có chung chiều cao hạ từ đỉnh D và đáy$AE = \frac{1}{3}AB$)
Suy ra SAED = $\frac{1}{3} \times 72 = 24$ (cm2)
2. Ta có SDEB = $\frac{2}{3}$SDAB = $\frac{2}{3}$SCDB nên chiều cao hạ từ E xuống BD bằng $\frac{2}{3}$ chiều cao từ C xuống BD.
Suy ra SEDG = $\frac{2}{3}$SCDG = $\frac{2}{5}$SECD
SECD = AD x DC : 2 = SABCD : 2 = 144 : 2 = 72 (cm2)
SEDG = $\frac{2}{5} \times 72 = 28,8$ (cm2)
SAEGD = 24 + 28,8 = 52,8 (cm2)
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi vào lớp 6 môn Toán trường Nguyễn Tất Thành năm 2023 timdapan.com"