Đề thi vào lớp 6 môn Toán trường Lương Thế Vinh năm 2024

Đề thi

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI TRƯỜNG THCS & THPT LƯƠNG THẾ VINH

ĐỀ TUYỂN SINH VÀO LỚP 6 NĂM HỌC: 2024 – 2025 Môn thi: Toán Thời gian: 60 phút

 

TT	Câu hỏi	Trả lời
1	Tìm a biết: 2 × a - $2\frac{3}{5}$= $\frac{{47}}{5}$
2	Tìm số tự nhiên nhỏ nhất chia hết cho 5 và 7. (Đề khác Tìm số tự nhiên nhỏ nhất có hai chữ số chia hết cho 5 và 7).
3	Tính: 52,39 - 28,23 - 21,77 = ....
4	Tính: $\frac{3}{7} + \frac{8}{5} + \frac{4}{7} - \frac{{48}}{{30}} = ...$
5	Điền số thích hợp vào chỗ chấm: 1 tấn 3 tạ = …kg.
6	Tìm hai số tự nhiên có tổng là 1989 và tỉ số là $\frac{4}{5}$
7	Hai năm trước mẹ gấp 8 lần tuổi con, hai năm sau tổng số tuổi mẹ và tuổi con là 44. Tìm số tuổi mỗi người hiện nay.
8	Tìm số tự nhiên có 4 chữ số, biết rằng nếu xóa chữ số hàng chục và hàng đơn vị thì được số mới kém số đã cho 4 059 đơn vị.
9	Tìm số lớn nhất có các chữ số khác nhau sao cho tích các chữ số bằng 105.
10	Trường THCS & THPT Lương Thế Vinh bán xúc xích để lập quỹ ủng hộ người khó khăn. Biết buổi sáng bán với giá 10 000 đồng một cây xúc xích. Buổi chiều do hạ giá nên số xúc xích bán được tăng 25%, số tiền thu về tăng 12,5% so với buổi sáng. Tính số tiền bán một cây xúc xích buổi chiều.
11	Cho diện tích mỗi hình vuông bé là 1 cm². Tính tổng diện tích các hình vuông có chứa con mèo.
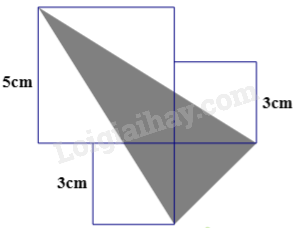
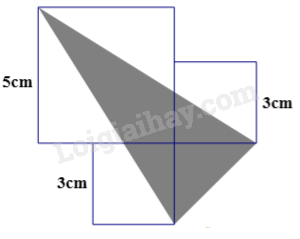
12	Cho cạnh hình vuông lớn là 5cm, cạnh của hai hình vuông nhỏ là 3 cm. Tính diện tích phần tô đậm.
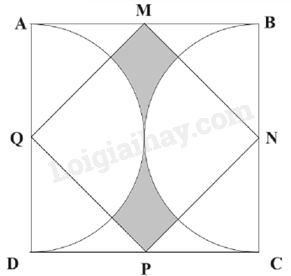
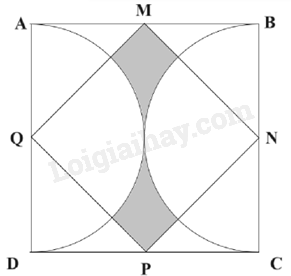
13	Cho hình vuông ABCD có M, N.P, Q lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ. Tính diện tích phần tô màu có trong hình vẽ, biết chu vi hình vuông ABCD là 24cm.
14	Tính hiệu của tống 50 số lẻ đầu tiên với 50 số tự nhiên đầu tiên.
15	Trung bình cộng của 4 số chẵn liên tiếp là 27, tìm 4 số đó.
16	Lớp 5A có 32 học sinh. Số học sinh nam bằng $\frac{3}{8}$ số học sinh. Tính số học sinh nữ.
17	Một đội công nhân 18 người hoàn thành công việc trong 12 ngày. Hỏi 17 nếu muốn hoàn thành công việc trong 9 ngày thì phải bổ sung bao nhiêu công nhân? (Biệt năng suất làm việc mỗi người là như nhau).
18	Một bể bơi dạng hình hộp chữ nhật có chiều dài 20,5m, chiều rộng 16,2m. Khi đổ 298,89 m3 nước vào bể thì mực nước có chiều cao bằng $\frac{3}{4}$ chiều cao của bể. Tính chiều cao của bể bơi.
19	Đang cập nhật đề
20	Đang cập nhật đề

---

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

Đáp án:

TT	Câu hỏi	Trả lời
1	Tìm a biết: 2 × a - $2\frac{3}{5}$= $\frac{{47}}{5}$	a = 6
2	Tìm số tự nhiên nhỏ nhất chia hết cho 5 và 7. (Đề khác Tìm số tự nhiên nhỏ nhất có hai chữ số chia hết cho 5 và 7).	35
3	Tính: 52,39 - 28,23 - 21,77 = ....	2,39
4	Tính: $\frac{3}{7} + \frac{8}{5} + \frac{4}{7} - \frac{{48}}{{30}} = ...$	1
5	Điền số thích hợp vào chỗ chấm: 1 tấn 3 tạ = …kg.	1 300
6	Tìm hai số tự nhiên có tổng là 1989 và tỉ số là $\frac{4}{5}$	1 105 và 884
7	Hai năm trước mẹ gấp 8 lần tuổi con, hai năm sau tổng số tuổi mẹ và tuổi con là 44. Tìm số tuổi mỗi người hiện nay.	Mẹ 34 tuổi, con 6 tuổi
8	Tìm số tự nhiên có 4 chữ số, biết rằng nếu xóa chữ số hàng chục và hàng đơn vị thì được số mới kém số đã cho 4 059 đơn vị.	4 100; 4 099
9	Tìm số lớn nhất có các chữ số khác nhau sao cho tích các chữ số bằng 105.	7 531
10	Trường THCS & THPT Lương Thế Vinh bán xúc xích để lập quỹ ủng hộ người khó khăn. Biết buổi sáng bán với giá 10 000 đồng một cây xúc xích. Buổi chiều do hạ giá nên số xúc xích bán được tăng 25%, số tiền thu về tăng 12,5% so với buổi sáng. Tính số tiền bán một cây xúc xích buổi chiều.	9 000 đồng
11	Cho diện tích mỗi hình vuông bé là 1 cm². Tính tổng diện tích các hình vuông có chứa con mèo.	85 cm²
12	Cho cạnh hình vuông lớn là 5cm, cạnh của hai hình vuông nhỏ là 3 cm. Tính diện tích phần tô đậm.	19,5 cm²
13	Cho hình vuông ABCD có M, N.P, Q lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ. Tính diện tích phần tô màu có trong hình vẽ, biết chu vi hình vuông ABCD là 24cm.	3,87 cm²
14	Tính hiệu của tống 50 số lẻ đầu tiên với 50 số tự nhiên đầu tiên.	1 275
15	Trung bình cộng của 4 số chẵn liên tiếp là 27, tìm 4 số đó.	24, 26, 28, 30.
16	Lớp 5A có 32 học sinh. Số học sinh nam bằng $\frac{3}{8}$ số học sinh. Tính số học sinh nữ.	20
17	Một đội công nhân 18 người hoàn thành công việc trong 12 ngày. Hỏi 17 nếu muốn hoàn thành công việc trong 9 ngày thì phải bổ sung bao nhiêu công nhân? (Biệt năng suất làm việc mỗi người là như nhau).	6 công nhân
18	Một bể bơi dạng hình hộp chữ nhật có chiều dài 20,5m, chiều rộng 16,2m. Khi đổ 298,89 m3 nước vào bể thì mực nước có chiều cao bằng $\frac{3}{4}$ chiều cao của bể. Tính chiều cao của bể bơi.	1,2 m

Lời giải chi tiết

Câu 1. Tìm a biết: 2 × a - $2\frac{3}{5}$= $\frac{{47}}{5}$

Phương pháp

Tìm số

- Số bị trừ = Hiệu + Số trừ

- Thừa số = Tích : Thừa số

Lời giải

2 × a - $2\frac{3}{5}$= $\frac{{47}}{5}$

2 × a - $\frac{{13}}{5}$= $\frac{{47}}{5}$

2 × a = $\frac{{47}}{5}$+ $\frac{{13}}{5}$

2 × a = 12

a = 6

Đáp án: a = 6

Câu 2. Tìm số tự nhiên nhỏ nhất chia hết cho 5 và 7.

(Đề khác Tìm số tự nhiên nhỏ nhất có hai chữ số chia hết cho 5 và 7).

Phương pháp

Lời giải

Các số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5

Các số tự nhiên chia hết cho cả 5 và 7 là: 0; 35; 70; 105; ...

Vậy số tự nhiên nhỏ nhất có 2 chữ số chia hết cho cả 5 và 7 là 35.

Đáp án: 35

Câu 3. Tính: 52,39 - 28,23 - 21,77 = ....

Phương pháp

Thực hiện phép tính trừ với số thập phân.

Lời giải

52,39 - 28,23 - 21,77 = 52,39 – (28,23 - 21,77) = 52,39 – 50 = 2,39

Đáp án: 2,39

Câu 4. Tính: $\frac{3}{7} + \frac{8}{5} + \frac{4}{7} + \frac{{48}}{{30}} = ...$

Phương pháp

Thực hiện phép tính với phân số.

- Rút gọn

- Nhóm các phân số cùng mẫu số rồi tính

Lời giải

$\frac{3}{7} + \frac{8}{5} + \frac{4}{7} - \frac{{48}}{{30}} = \frac{3}{7} + \frac{8}{5} + \frac{4}{7} - \frac{8}{5} = (\frac{3}{7} + \frac{4}{7}) + (\frac{8}{5} - \frac{8}{5}) = 1 + 0 = 1$

Đáp án: 1

Câu 5. Điền số thích hợp vào chỗ chấm: 1 tấn 3 tạ = …kg.

Phương pháp

Áp dụng cách đổi:

1 tấn = 1 000 kg

1 tạ = 100 kg

Lời giải

1 tấn 3 tạ = 1 300 kg.

Đáp án: 1 300

Câu 6. Tìm hai số tự nhiên có tổng là 1989 và tỉ số là $\frac{4}{5}$

Phương pháp

Tìm hai số khi biết tổng và tỉ số của hai số đó

- Tìm tổng số phần bằng nhau và tìm giá trị của 1 phần.

- Tìm số lớn = Giá trị của một phần x số phần của số lớn

- Tìm số bé = Tổng hai số - số lớn

Lời giải

Theo đề bài, coi số lớn là 5 phần bằng nhau và số 5 bé là 4 phần như vậy.

Tổng số phần bằng nhau là: 5 + 4 = 9 (phần)

Số lớn là: 1989 : 9 × 5 = 1 105

Số bé là: 1989 – 1 105 = 884

Đáp án: 1 105 và 884

Câu 7. Hai năm trước mẹ gấp 8 lần tuổi con, hai năm sau tổng số tuổi mẹ và tuổi con là 44. Tìm số tuổi mỗi người hiện nay.

Phương pháp

Tìm tổng số tuổi của mẹ và con hai năm trước = tổng số tuổi mẹ và tuổi con hai năm sau - 2 × 4

Tìm hai số khi biết tổng và tỉ số của hai số đó

- Tìm tổng số phần bằng nhau và tìm giá trị của 1 phần.

- Tìm số lớn = Giá trị của một phần x số phần của số lớn

- Tìm số bé = Tổng hai số - số lớn

Lời giải

Tổng số tuổi của mẹ và con hai năm trước là:

44 - 2 × 4 = 36 (tuổi)

Coi tuổi con hai năm trước là 1 phần thì tuổi mẹ hai năm trước là 8 phần như thế

Tuổi con hai năm trước là:

36 : (1 + 8) × 4 = 4 (tuổi)

Tuổi mẹ hai năm trước là:

36 - 4 = 32 (tuổi)

Tuổi con hiện nay là:

4 + 2 = 6 (tuổi)

Tuổi mẹ hiện nay là:

32 + 2 = 34 (tuổi)

Đáp án: Mẹ 34 tuổi, con 6 tuổi

Câu 8. Tìm số tự nhiên có 4 chữ số, biết rằng nếu xóa chữ số hàng chục và hàng đơn vị thì được số mới kém số đã cho 4 059 đơn vị.

Phương pháp

Bài toán về cấu tạo số

Sử dụng kiến thức về dấu hiệu chia hết

Lời giải

Gọi số tự nhiên cần tìm là: $\overline {abcd} $ (a, b, c, d là các chữ số và a khác 0)

Theo đề bài, ta có:

$\overline {abcd} $- $\overline {ab} $ = 4 059

$\overline {ab} $× 100 + $\overline {cd} $ - $\overline {ab} $ = 4 059

$\overline {ab} $× 99 + $\overline {cd} $ = 4 059

$ \Rightarrow $$\overline {cd} $ = 4 059 - $\overline {ab} $× 99 > 0

Vì 4 059 và $\overline {ab} $× 99  cùng chia hết cho 99

$ \Rightarrow $$\overline {cd} $ chia hết cho 99 nên $\overline {cd} $ = 00 hoặc $\overline {cd} $ = 99

Với $\overline {cd} $ = 00 $ \Rightarrow $$\overline {ab} $× 99 + 00 = 4 059 $ \Rightarrow $$\overline {ab} $ = 41. Ta có số 4 100

Với $\overline {cd} $ = 99 $ \Rightarrow $$\overline {ab} $× 99 + 99 = 4 059 $ \Rightarrow $$\overline {ab} $ = 40. Ta có số 4 099

Vậy các số cần tìm là 4 100; 4 099

Đáp án: 4 100; 4 099

Câu 9. Tìm số lớn nhất có các chữ số khác nhau sao cho tích các chữ số bằng 105.

Phương pháp

- Phân tích số 105 thành tích của các số

- Sắp xếp các số đó để tạo thành số lớn nhất có các chữ số khác nhau.

Lời giải

(Lưu ý: Các mã đề là tìm số lớn nhất có 3 chữ số khác nhau...)

Muốn lập được số lớn nhất có các chữ số khác nhau ta cần lập được số có nhiều chữ số khác nhau nhất có thể.

Ta có: 105 = 1 × 3 × 5 × 7

Vậy ta lập được số lớn nhất có các chữ số khác nhau thỏa mãn tích các chữ số bằng 105 là: 7531

Đáp án: 7531

Câu 10. Trường THCS & THPT Lương Thế Vinh bán xúc xích để lập quỹ ủng hộ người khó khăn. Biết buổi sáng bán với giá 10 000 đồng một cây xúc xích. Buổi chiều do hạ giá nên số xúc xích bán được tăng 25%, số tiền thu về tăng 12,5% so với buổi sáng. Tính số tiền bán một cây xúc xích buổi chiều.

Phương pháp

Bài toán về tỉ số phần trăm

Lời giải

Số lượng xúc xích bán được buổi chiều bằng:

100% + 25% = 125% (số lượng xúc xích bán được buổi sáng)

Số tiền thu được buổi chiều bằng: 100% + 12,5% = 112,5% (số tiền thu được buổi sáng)

Số tiền bán 1 cây xúc xích buổi chiều bằng:

112,5% : 125% = 90% (số tiền bán 1 cây xúc xích buổi sáng)

Số tiền bán 1 cây xúc xích buổi chiều là:

10 000 × 90 : 100 = 9 000 (đồng)

Đáp án: 9 000 đồng

Câu 11. Cho diện tích mỗi hình vuông bé là 1 cm². Tính tổng diện tích các hình vuông có chứa con mèo.

Phương pháp

Tìm số hình vuông có chứa con mèo ở các kích thước khác nhau

Tính tổng diện tích các hình vuông vừa tìm được

Lời giải

Ta có:

Số hình vuông kích thước 1 x 1 là: 1 hình

Số hình vuông kích thước 2 x 2 là: 4 hình

Số hình vuông kích thước 3 x 3 là: 4 hình

Số hình vuông kích thước 4 x 4 là 2 hình

Tổng diện tích các hình vuông có chứa con mèo là:

(1 × 1) × 1+ (2 × 2) × 4 + (3 × 3) × 4 + (4 × 4) × 2 = 85 (cm²)

Đáp án: 85 cm²

Câu 12. Cho cạnh hình vuông lớn là 5cm, cạnh của hai hình vuông nhỏ là 3 cm. Tính diện tích phần tô đậm.

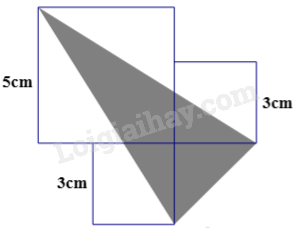
Phương pháp

- Chia hình tô đậm thành các hình đã biết cách tính diện tích

- Tính diện tích từng hình

Tính tổng diện tích các hình đó chính là diện tích hình tô đậm

Lời giải

Ta đánh dấu các điểm như hình dưới đây:

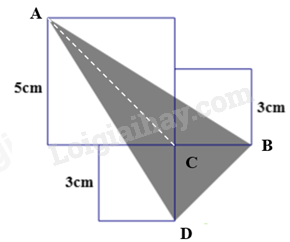
Diện tích phần tô đậm chính bằng tổng diện tích các tam giác ABC, ACD và BCD.

Diện tích tam giác ABC là:

5 × 3 : 2 = 7,5 (cm²)

Diện tích tam giác ADC là:

5 x 3 : 2 = 7,5 (cm²)

Diện tích tam giác BCD là:

3 x 3 : 2 = 4,5 (cm²)

Diện tích phần tô đậm là:

7,5 - 7,5 + 4,5 = 19,5 (cm²)

Đáp án: 19,5 cm²

Câu 13. Cho hình vuông ABCD có M, N.P, Q lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ. Tính diện tích phần tô màu có trong hình vẽ, biết chu vi hình vuông ABCD là 24cm.

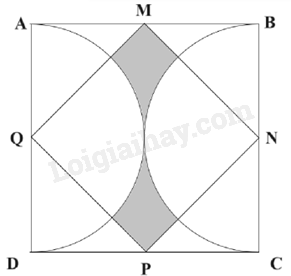
Phương pháp

Lời giải

Ta đánh số như sau:

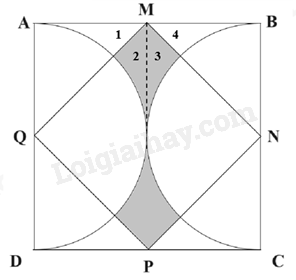
Ta thấy: Diện tích phần tô màu chính bằng tổng diện tích các phần (1), (2), (3), (4) và bằng hiệu diện tích hình vuông ABCD và diện tích hình tròn đường kính AD.

Cạnh hình vuông ABCD là: 24 : 6 = 6 (cm)

Diện tích hình vuông ABCD là: 6 × 6 = 36 (cm²)

Diện tích hình tròn đường kính AD là: (6 : 3) × (6 : 3) × 3,14 = 28,26 (cm²)

Diện tích phần tô màu là: (36 - 28,26) : 2 = 3,87 (cm²)

Đáp án: 3,87 cm²

Câu 14. Tính hiệu của tổng 50 số lẻ đầu tiên với 50 số tự nhiên đầu tiên.

Phương pháp

Số tự nhiên đầu tiên bắt đầu từ 0

- Áp dụng công thức:

Số số hạng của dãy số = (Số hạng cuối – số hạng đầu) : khoảng cách + 1

Tổng của dãy số cách đều = (số hạng đầu + số hạng cuối) x số số hạng : 2

- Tính tổng 50 số lẻ đầu tiên

- Tính tổng 50 số tự nhiên đầu tiên

- Tính hiệu của tổng 50 số lẻ đầu tiên với 50 số tự nhiên đầu tiên.

Lời giải

Tổng của 50 số tự nhiên đầu tiên là:

0 + 1 + 2 + 3 + 4 + ... + 49 = (49 + 0) × 50 : 2 = 1 225

Số lẻ đầu tiên là 1. Số lẻ thứ 50 là: 1 + (50 - 1) ×  2 = 99

Tổng của 50 số lẻ đầu tiên là: (1 + 99) × 50 : 2 = 2 500

Hiệu của tổng 50 số lẻ đầu tiên với 50 số tự nhiên đầu tiên là:

2 500 – 1 225 = 1 275

Đáp án: 1 275

Câu 15. Trung bình cộng của 4 số chẵn liên tiếp là 27, tìm 4 số đó.

Phương pháp

Lời giải

Trung bình cộng của số đầu và số cuối bằng trung bình cộng của 4 số chẵn liên tiếp và bằng 27

Tổng của số chẵn đầu và số chẵn cuối là 27 × 2 = 54

Hiệu số chẵn đầu và số chẵn cuối là: (4 – 1) × 3 = 6

Số chẵn đầu là: (54 – 6) : 2 = 24

Vậy 4 số chẵn liên tiếp là: 24, 26, 28, 30.

Đáp án: 24, 26, 28, 30.

Câu 16. Lớp 5A có 32 học sinh. Số học sinh nam bằng $\frac{3}{8}$ số học sinh. Tính số học sinh nữ.

Phương pháp

Lời giải

Số học sinh nam của lớp 5A là 32 × $\frac{3}{8}$= 12 (học sinh)

Số học sinh nữ của lớp 5A là: 32 – 12 = 20 (học sinh)

Đáp án: 20

Câu 17. Một đội công nhân 18 người hoàn thành công việc trong 12 ngày. Hỏi nếu muốn hoàn thành công việc trong 9 ngày thì phải bổ sung bao nhiêu công nhân? (Biệt năng suất làm việc mỗi người là như nhau).

Phương pháp

Tính số ngày 1 công nhân hoàn thành công việc = Tổng số công nhân ban đầu × Tổng số ngày hoàn thành công việc

Số công nhân để hoàn thành công việc trong 9 ngày = số ngày 1 công nhân hoàn thành công việc : 9

Tính số công nhân cần bổ sung thêm = Số công nhân để hoàn thành công việc trong 9 ngày - Tổng số công nhân ban đầu

Lời giải

1 công nhân hoàn thành công việc trong số ngày là: 12 × 18 = 216 (ngày)

Muốn hoàn thành công việc trong 9 ngày thì cần số công nhân là: 216 : 9 = 24 (công nhân)

Cần bổ sung số công nhân là: 24 – 18 = 6 (công nhân)

Đáp án: 6 công nhân

Câu 18. Một bể bơi dạng hình hộp chữ nhật có chiều dài 20,5m, chiều rộng 16,2m. Khi đổ 298,89 m³ nước vào bể thì mực nước có chiều cao bằng $\frac{3}{4}$ chiều cao của bể. Tính chiều cao của bể bơi.

Phương pháp

Diện tích đáy bể = Chiều dài × Chiều rộng

Chiều cao mực nước hiện có = Thể tích nước : Diện tích đáy bể

Chiều cao của bể bơi = Chiều cao mực nước hiện có : $\frac{3}{4}$

Lời giải

Diện tích đáy bể là: 20,5 × 16,2 = 332,1 (m²)

Chiều cao mực nước hiện có: 289,89 : 332,1 = 0,9 (m)

Chiều cao của bể bơi: 0,9 : 3 × 4 = 1,2 (m)

Đáp án: 1,2 m