Đề thi vào 10 môn Toán Ninh Thuận năm 2020
Câu 1: a) Tìm
Đề bài
Câu 1:
a) Tìm \(x\) để biểu thức \(A = \sqrt {2x - 3} \) có nghĩa
b) Giải phương trình \({x^2} + 5x + 3 = 0\)
Câu 2:
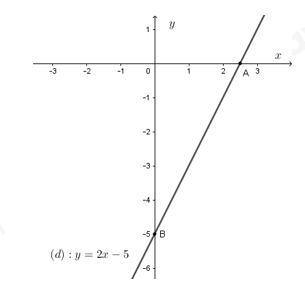
Cho hàm số \(y = 2x - 5\) có đồ thị là đường thẳng \(\left( d \right)\)
a) Gọi \(A\),\(B\) lần lượt là giao điểm của \(\left( d \right)\) với các trục tọa độ \(Ox,Oy\). Tìm tọa độ các điểm A, B và vẽ đường thẳng \(\left( d \right)\) trong mặt phẳng tọa độ \(Oxy.\)
b) Tính diện tích tam giác \(OAB.\)
Câu 3:
a) Rút gọn biểu thức: \(P = \dfrac{{x - 2\sqrt x + 1}}{{\sqrt x - 1}}.\left( {\dfrac{{x + \sqrt x }}{{\sqrt x + 1}} + 1} \right)\) (với \(x \ge 0\) và \(x \ne 1\))
b) Cho \(a > 0,b > 0.\) Chứng minh rằng: \(\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\)
Câu 4:
Cho đường tròn tâm O đường kính \(AB = 2R.\) Vẽ dây cung \(CD\) vuông góc với \(AB\) tại \(I\) (\(I\) nằm giữa \(A\) và \(O\)). Lấy điểm \(E\) trên cung nhỏ \(BC\) (\(E\) khác \(B\) và \(C\)), \(AE\) cắt \(CD\) tại \(F.\)
a) Chứng minh tứ giác \(BEFI\) nội tiếp trong một đường tròn
b) Tính độ dài cạnh \(AC\) theo \(R\) và \(\angle ACD\) khi \(\angle BAC = {60^0}.\)
c) Chứng minh khi điểm \(E\) chạy trên cung nhỏ \(BC\) thì tâm đường tròn ngoại tiếp tam giác \(CEF\) luôn thuộc một đường thẳng cố định.
Lời giải
Câu 1 (2 điểm)
Cách giải:
a) Tìm \(x\) để biểu thức \(A = \sqrt {2x - 3} \) có nghĩa
Ta có biểu thức \(A = \sqrt {2x - 3} \) có nghĩa khi \(2x - 3 \ge 0 \Leftrightarrow 2x \ge 3 \Leftrightarrow x \ge \dfrac{3}{2}\)
Vậy với \(x \ge \dfrac{3}{2}\) thì biểu thức \(A = \sqrt {2x - 3} \) có nghĩa
b) Giải phương trình \({x^2} + 5x + 3 = 0\)
Ta có: \(\Delta = {5^2} - 4.1.3 = 13 > 0\)
Nên phương trình đã cho có hai nghiệm phân biệt \({x_1} = \dfrac{{ - 5 + \sqrt {13} }}{2};{x_2} = \dfrac{{ - 5 - \sqrt {13} }}{2}\)
Vậy phương trình đã cho có hai nghiệm phân biệt \({x_1} = \dfrac{{ - 5 + \sqrt {13} }}{2};{x_2} = \dfrac{{ - 5 - \sqrt {13} }}{2}\)
Câu 2 (2 điểm)
Cách giải:
Cho hàm số \(y = 2x - 5\) có đồ thị là đường thẳng \(\left( d \right)\)
a) Gọi \(A\),\(B\) lần lượt là giao điểm của \(\left( d \right)\) với các trục tọa độ \(Ox,Oy\). Tìm tọa độ các điểm A, B và vẽ đường thẳng \(\left( d \right)\) trong mặt phẳng tọa độ \(Oxy.\)
Vì A là giao điểm của \(\left( d \right)\) và trục \(Ox\) nên \(A\left( {x;0} \right)\)
Ta có \(A\left( {x;0} \right) \in \left( d \right)\) nên \(0 = 2x - 5 \Leftrightarrow x = \dfrac{5}{2} \Rightarrow A\left( {\dfrac{5}{2};0} \right)\)
Vì B là giao điểm của \(\left( d \right)\) và trục \(Oy\) nên \(B\left( {0;y} \right)\)
Ta có \(B\left( {0;y} \right) \in \left( d \right)\) nên \(y = 2.0 - 5 \Leftrightarrow y = - 5 \Rightarrow B\left( {0; - 5} \right)\)
Vậy \(A\left( {\dfrac{5}{2};0} \right),B\left( {0; - 5} \right)\)
+) Vẽ đường thẳng \(\left( d \right):y = 2x - 5\)
Với \(x = 0 \Rightarrow y = - 5\) suy ra \(B\left( {0; - 5} \right)\)
Với \(y = 0 \Rightarrow x = \dfrac{5}{2}\) suy ra \(A\left( {\dfrac{5}{2};0} \right)\)
Đường thẳng đi qua hai điểm \(A\left( {\dfrac{5}{2};0} \right),B\left( {0; - 5} \right)\) là đồ thị hàm số \(y = 2x - 5.\)
b) Tính diện tích tam giác \(OAB.\)
Theo câu a) ta có: \(A\left( {\dfrac{5}{2};0} \right),B\left( {0; - 5} \right)\) nên \(OA = \left| {\dfrac{5}{2}} \right| = \dfrac{5}{2};OB = \left| { - 5} \right| = 5\)
Tam giác \(OAB\) vuông tại \(O\) nên diện tích tam giác \(OAB\) là: \({S_{OAB}} = \dfrac{1}{2}OA.OB\) \( = \dfrac{1}{2}.\dfrac{5}{2}.5 = \dfrac{{25}}{4}\) (đvdt)
Câu 3 (2 điểm)
Cách giải:
a) Rút gọn biểu thức: \(P = \dfrac{{x - 2\sqrt x + 1}}{{\sqrt x - 1}}.\left( {\dfrac{{x + \sqrt x }}{{\sqrt x + 1}} + 1} \right)\) (với \(x \ge 0\) và \(x \ne 1\))
Ta có: \(P = \dfrac{{x - 2\sqrt x + 1}}{{\sqrt x - 1}}.\left( {\dfrac{{x + \sqrt x }}{{\sqrt x + 1}} + 1} \right)\)
\( = \dfrac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x - 1}}.\left( {\dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}} + 1} \right)\)
\( = \left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right) = x - 1\)
Vậy \(P = x - 1\) với \(x \ge 0\) và \(x \ne 1\)
b) Cho \(a > 0,b > 0.\) Chứng minh rằng: \(\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\)
Ta có:
\(\begin{array}{l}\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\\ \Leftrightarrow \dfrac{{a + b}}{{ab}} \ge \dfrac{4}{{a + b}}\\ \Leftrightarrow \dfrac{{a + b}}{{ab}} - \dfrac{4}{{a + b}} \ge 0\\ \Leftrightarrow \dfrac{{{{\left( {a + b} \right)}^2} - 4ab}}{{ab\left( {a + b} \right)}} \ge 0\end{array}\)
\( \Leftrightarrow {\left( {a + b} \right)^2} - 4ab \ge 0\) (do \(a > 0,b > 0 \Rightarrow ab\left( {a + b} \right) > 0\))
\(\begin{array}{l} \Leftrightarrow {a^2} + {b^2} + 2ab - 4ab \ge 0\\ \Leftrightarrow {a^2} + {b^2} - 2ab \ge 0\end{array}\)
\( \Leftrightarrow {\left( {a - b} \right)^2} \ge 0\) (luôn đúng với mọi \(a,b\))
Suy ra \(\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\) với \(a > 0,b > 0.\)
Câu 4 (4 điểm)
Cách giải:
Cho đường tròn tâm O đường kính \(AB = 2R.\) Vẽ dây cung \(CD\) vuông góc với \(AB\) tại \(I\) (\(I\) nằm giữa \(A\) và \(O\)). Lấy điểm \(E\) trên cung nhỏ \(BC\) (\(E\) khác \(B\) và \(C\)), \(AE\) cắt \(CD\) tại \(F.\)
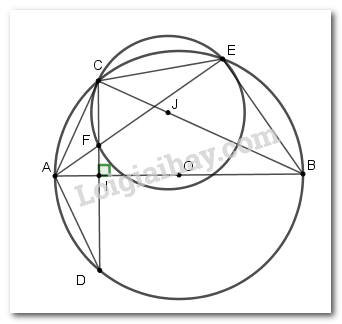
a) Chứng minh tứ giác \(BEFI\) nội tiếp trong một đường tròn
Xét đường tròn \(\left( O \right)\) có \(\angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
Lại có \(\angle FIB = {90^0}\) (do \(CD \bot AB\) tại \(I\))
Xét tứ giác \(BEFI\) có: \(\angle FEB + \angle FIB = {90^0} + {90^0} = {180^0}\) mà hai góc \(\angle FEB,\angle FIB\) đối nhau nên tứ giác \(BEFI\) nội tiếp (dhnb).
b) Tính độ dài cạnh \(AC\) theo \(R\) và \(\angle ACD\) khi \(\angle BAC = {60^0}.\)
Xét đường tròn \(\left( O \right)\) có \(\angle ACB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
Xét tam giác \(ABC\) vuông tại \(C\) ta có: \(\angle ABC = {90^0} - \angle BAC = {90^0} - {60^0} = {30^0}\)
Ta có: \(\cos \angle BAC = \dfrac{{AC}}{{AB}} \Leftrightarrow AC = AB.\cos \angle BAC\) \( = 2R.\cos {60^0} = 2R.\dfrac{1}{2} = R.\)
Xét đường tròn \(\left( O \right)\) có \(AB \bot CD\) tại \(I\) nên \(I\) là trung điểm của dây \(CD\) (quan hệ giữa đường kính và dây cung)
Hay \(AB\) là đường trung trực của đoạn \(CD\) , suy ra \(AC = AD\)
Do đó cung \(AC = \) cung \(AD\) (hai dây bằng nhau căng hai cung bằng nhau)
Xét đường tròn \(\left( O \right)\) có \(\angle ACD = \angle ABC = {30^0}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AC\) và \(AD\))
Nên \(\angle ACD = {30^0}.\)
Vậy \(AC = R,\angle ACD = {30^0}\) khi \(\angle BAC = {60^0}.\)
c) Chứng minh khi điểm \(E\) chạy trên cung nhỏ \(BC\) thì tâm đường tròn ngoại tiếp tam giác \(CEF\) luôn thuộc một đường thẳng cố định.
Xét đường tròn \(\left( O \right)\) có \(\angle CEA = \angle ACD\) (hai góc nội tiếp chắn hai cung bằng nhau \(CA\) và \(AD\))
Xét đường tròn ngoại tiếp tam giác \(CEF\) có \(\angle CEF = \angle ACF\)
Mà \(\angle CEF\) là góc nội tiếp chắn cung \(CF\)
Suy ra \(AC\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(CEF\)
Gọi \(J\) là tâm đường tròn ngoại tiếp tam giác \(CEF\), suy ta \(JC \bot AC\) tại \(C\) (do \(AC\) là tiếp tuyến)
Lại có \(\angle ACB = {90^0}\) (cmt) hay \(AC \bot BC\)
Suy ra \(J \in BC\)
Hay tâm đường tròn ngoại tiếp tam giác \(CEF\) luôn thuộc đường thẳng \(BC\) cố định.
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi vào 10 môn Toán Ninh Thuận năm 2020 timdapan.com"