Đề thi vào 10 môn Toán Ninh Thuận năm 2019
Bài 1 (2 điểm) Giải bất phương trình và hệ phương trình sau:
Đề bài
Bài 1 (2 điểm) Giải bất phương trình và hệ phương trình sau:
\(a)7x - 2 > 4x + 3\\ b)\left\{ \begin{array}{l}3x + y = 1\\x - 2y = 5\end{array} \right.\)
Bài 2 (2 điểm) Cho parabol \(\left( P \right):\,\,\,y = 2{x^2}\) và đường thẳng \(d:\,\,\,y = 3x + 2.\)
a) Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ \(Oxy.\)
b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right).\)
Bài 3 (2 điểm)
a) Rút gọn biểu thức: \(P = \left( {\dfrac{{\sqrt a }}{2} - \dfrac{1}{{2\sqrt a }}} \right).\left( {\dfrac{{\sqrt a - 1}}{{\sqrt a + 1}} - \dfrac{{\sqrt a + 1}}{{\sqrt a - 1}}} \right),\,\,\,a > 1,\,\,a \ne 1.\)
b) Chứng minh rằng phương trình: \({x^2} - 2\left( {m - 1} \right)x + 2m - 4 = 0\) luôn có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\) Tìm giá trị nhỏ nhất của biểu thức: \(A = x_1^2 + x_2^2.\)
Bài 4 (4 điểm) Cho tam giác \(ABC\) vuông tại \(C\) nội tiếp trong đường tròn tâm \(O,\) đường kính \(AB = 2R,\,\,\angle ABC = {60^0}.\) Gọi \(H\) là chân đường cao hạ từ \(C\) xuống \(AB,\,\,K\) là trung điểm đoạn thẳng \(AC.\) Tiếp tuyến tại \(B\) của đường tròn tâm \(O\) cắt \(AC\) kéo dài tại điểm \(D.\)
a) Chứng minh tứ giác \(CHOK\) nội tiếp trong một đường tròn.
b) Chứng minh rằng: \(AC.AD = 4{R^2}.\)
c) Tính theo \(R\) diện tích của phần tam giác \(ABD\) nằm ngoài hình tròn tâm \(O.\)
Lời giải
Bài 1 (2,0 điểm) (TH):
Phương pháp:
a) Giải bất phương trình bằng quy tắc chuyển vế đổi dấu.
b) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.
Cách giải:
a) \(7x - 2 > 4x + 3\).
\(\begin{array}{l} \Leftrightarrow 7x - 4x > 3 + 2\\ \Leftrightarrow 3x > 5 \Leftrightarrow x > \dfrac{5}{3}\end{array}\)
Vậy nghiệm của bất phương trình là \(x > \dfrac{5}{3}\).
b) \(\left\{ \begin{array}{l}3x + y = 1\\x - 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x + 2y = 2\\x - 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 7\\y = 1 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1 - 3 = - 2\end{array} \right.\).
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {1; - 2} \right)\).
Bài 2 (2,0 điểm) (VD):
Phương pháp:
a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục.
b) Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta > \,\,0\,\,\,\left( {\Delta ' > 0} \right).\)
+) Sử dụng định lý Vi-ét để tìm giá trị nhỏ nhất của biểu thức.
Cách giải:
a) Vẽ parabol \(\left( P \right):\,\,y = 2{x^2}\).
Bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = 2{x^2}\) |
\(8\) |
2 |
0 |
2 |
8 |
\( \Rightarrow \) Đồ thị hàm số \(y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;8} \right);\,\,\left( { - 1;2} \right);\,\,\left( {0;0} \right);\,\,\left( {1;2} \right);\,\,\left( {2;8} \right)\).
Vẽ đồ thị:
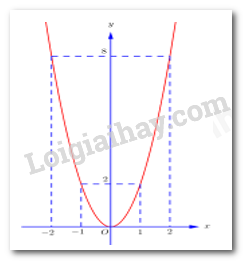
b) Xét phương trình hoành độ giao điểm của hai đồ thị hàm số ta được:
\(\begin{array}{l}\,\,\,\,\,\,\,\,2{x^2} = 3x + 2 \Leftrightarrow 2{x^2} - 3x - 2 = 0\\ \Leftrightarrow 2{x^2} - 4x + x - 2 = 0 \Leftrightarrow 2x\left( {x - 2} \right) + \left( {x - 2} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {2x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\2x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = {2.2^2} = 8\\x = \dfrac{{ - 1}}{2} \Rightarrow y = 2.{\left( { - \dfrac{1}{2}} \right)^2} = \dfrac{1}{2}\end{array} \right.\end{array}\)
Vậy giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(A\left( {2;8} \right)\) và \(B\left( { - \dfrac{1}{2};\dfrac{1}{2}} \right)\).
Bài 3 (VD) (2 điểm)
Phương pháp:
a) Quy đồng mẫu thức, khai tiển và thu gọn \(P\).
b) +) Phương trình luôn có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0,\forall m\).
+) Sử dụng định lý Vi-et, đưa \(A\) về biểu thức ẩn \(m\). Tìm GTNN của \(A\) và kết luận.
Cách giải:
a) \(P = \left( {\dfrac{{\sqrt a }}{2} - \dfrac{1}{{2\sqrt a }}} \right).\left( {\dfrac{{\sqrt a - 1}}{{\sqrt a + 1}} - \dfrac{{\sqrt a + 1}}{{\sqrt a - 1}}} \right)\) với \(a > 0\) và \(a \ne 1\).
Điều kiện: \(a > 0,\,\,a \ne 1.\)
\(\begin{array}{l}P = \left( {\dfrac{{\sqrt a }}{2} - \dfrac{1}{{2\sqrt a }}} \right).\left( {\dfrac{{\sqrt a - 1}}{{\sqrt a + 1}} - \dfrac{{\sqrt a + 1}}{{\sqrt a - 1}}} \right) = \dfrac{{a - 1}}{{2\sqrt a }}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2} - {{\left( {\sqrt a + 1} \right)}^2}}}{{\left( {\sqrt a - 1} \right)\left( {\sqrt a + 1} \right)}}\\ = \dfrac{{a - 1}}{{2\sqrt a }}.\dfrac{{a - 2\sqrt a + 1 - a - 2\sqrt a - 1}}{{a - 1}} = \dfrac{{a - 1}}{{2\sqrt a }}.\dfrac{{ - 4\sqrt a }}{{a - 1}} = - 2.\end{array}\)
Vậy \(P = - 2\).
b) Chứng minh rằng phương trình \({x^2} - 2\left( {m - 1} \right)x + 2m - 4 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\) Tìm giá trị nhỏ nhất của biểu thức \(A = x_1^2 + x_2^2.\)
Ta có: \(\Delta ' = {\left( {m - 1} \right)^2} - \left( {2m - 4} \right) = {m^2} - 2m + 1 - 2m + 4 = {m^2} - 4m + 5\)
\( = \left( {{m^2} - 4m + 4} \right) + 1 = {\left( {m - 2} \right)^2} + 1 > 0,\forall m\)
\( \Rightarrow \) Phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) với mọi \(m\).
Theo định lý Vi – et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right)\\{x_1}{x_2} = 2m - 4\end{array} \right.\).
Theo đề bài ta có: \(A = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\).
\(\begin{array}{l} \Rightarrow A = 4{\left( {m - 1} \right)^2} - 2\left( {2m - 4} \right) = 4{m^2} - 8m + 4 - 4m + 8\\\,\,\,\,\,\,\, = 4{m^2} - 12m + 12 = 4{m^2} - 2.2m.3 + {3^2} + 3\\\,\,\,\,\,\,\, = {\left( {2m - 3} \right)^2} + 3.\end{array}\)
Ta có:\({\left( {2m - 3} \right)^2} \ge 0\,\,\,\forall m \Rightarrow A = {\left( {2m - 3} \right)^2} + 3 \ge 3\,\,\,\forall m\)
\( \Rightarrow A \ge 3\).
Dấu “=” xảy ra khi \(2m - 3 = 0 \Leftrightarrow m = \dfrac{3}{2}\).
Vậy \({A_{\min }} = 3\) khi \(m = \dfrac{3}{2}\).
Câu 4 (VD) (4 điểm)
Phương pháp:
a) Sử dụng các dấu hiệu nhận biết để chứng minh tứ giác nội tiếp.
b) Chứng minh các cặp tam giác đồng dạng để chứng minh đẳng thức.
c) Sử dụng định lý Ta-lét và các công thức tính viên phân và công thức diện tích tam giác để làm bài.
Cách giải:
a) \(CH \bot AB\,\,\left( {gt} \right) \Rightarrow \angle OHC = {90^0}\).
\(K\) là trung điểm của \(AC\) \( \Rightarrow OK \bot AC\) (quan hệ vuông góc giữa đường kính và dây) \( \Rightarrow \angle OKC = {90^0}\).
Xét tứ giác \(CHOK\) có \(\angle OHC + \angle OKC = {90^0} + {90^0} = {180^0}\).
Mà hai góc này ở vị trí đối diện nên tứ giác \(CHOK\) nội tiếp (đpcm).
b) Ta có: \(\angle C = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tam giác \(\Delta ACB\) và \(\Delta ABD\) có:
\(\angle ACB = \angle ABD = {90^0};\)
\(\angle BAD\) chung;
Suy ra (cạnh tương ứng)
\( \Rightarrow AC.AD = A{B^2} = 4{R^2}\) (đpcm).
c) Nối \(C\) với \(O\).
Tam giác \(OBC\) cân tại \(O\) có \(\angle OBC = {60^0}\,\,\left( {gt} \right)\) nên là tam giác đều cạnh \(OB = OC = BC = R\) và \(\angle BOC = {60^0}\).
\(CH \bot OB \Rightarrow H\) là trung điểm của \(OB \Rightarrow HB = \dfrac{R}{2}\).
Tam giác \(CHB\) vuông tại \(H\) \( \Rightarrow C{H^2} + H{B^2} = C{B^2}\) (Định lí Pytago)
\( \Rightarrow CH = \sqrt {C{B^2} - H{B^2}} = \sqrt {{R^2} - \dfrac{{{R^2}}}{4}} = \dfrac{{R\sqrt 3 }}{2}\)
\( \Rightarrow {S_{\Delta COB}} = \dfrac{1}{2}OB.CH = \dfrac{1}{2}.R.\dfrac{{R\sqrt 3 }}{2} = \dfrac{{{R^2}\sqrt 3 }}{4}\).
Diện tích hình quạt \({S_{qCOB}} = \dfrac{{60.\pi {R^2}}}{{360}} = \dfrac{{\pi {R^2}}}{6}\).
\( \Rightarrow \) Diện tích hình viên phân tạo bởi dây và cung nhỏ \(CB\) là \({S_{vp}} = {S_{qCOB}} - {S_{\Delta COB}} = \dfrac{{\pi {R^2}}}{6} - \dfrac{{{R^2}\sqrt 3 }}{4}\).
Diện tích tam giác \(ABC\) là: \({S_{\Delta ABC}} = \dfrac{1}{2}CH.AB = \dfrac{1}{2}.\dfrac{{R\sqrt 3 }}{2}.2R = \dfrac{{{R^2}\sqrt 3 }}{2}\).
Do \(CH//DB\) (cùng vuông góc \(AB\)) nên \(\dfrac{{AH}}{{AB}} = \dfrac{{CH}}{{DB}}\) (Định lí Ta-lét)
\( \Rightarrow DB = \dfrac{{AB.CH}}{{AH}} = \dfrac{{2R.\dfrac{{R\sqrt 3 }}{2}}}{{\dfrac{3}{4}.2R}} = \dfrac{{2R\sqrt 3 }}{3}\)
\( \Rightarrow \) Diện tích tam giác \(ABD\) là \({S_{\Delta ADB}} = \dfrac{1}{2}BA.BD = \dfrac{1}{2}2R.\dfrac{{2R\sqrt 3 }}{3} = \dfrac{{2{R^2}\sqrt 3 }}{3}\).
Vậy diện tích hình cần tính là:
\(\begin{array}{l}S = {S_{\Delta ABD}} - {S_{\Delta ABC}} - {S_{vp}}\\\,\,\,\, = \dfrac{{2{R^2}\sqrt 3 }}{3} - \dfrac{{{R^2}\sqrt 3 }}{2} - \left( {\dfrac{{\pi {R^2}}}{6} - \dfrac{{{R^2}\sqrt 3 }}{4}} \right)\\\,\,\,\, = \dfrac{{2{R^2}\sqrt 3 }}{3} - \dfrac{{{R^2}\sqrt 3 }}{2} - \dfrac{{\pi {R^2}}}{6} + \dfrac{{{R^2}\sqrt 3 }}{4} = \dfrac{{5{R^2}\sqrt 3 }}{{12}} - \dfrac{{\pi {R^2}}}{6}\end{array}\)
Vậy \(S = \dfrac{{5{R^2}\sqrt 3 }}{{12}} - \dfrac{{\pi {R^2}}}{6}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi vào 10 môn Toán Ninh Thuận năm 2019 timdapan.com"







