Đề thi vào 10 môn Toán Bến Tre năm 2019

Đề bài

Câu 1 (1,5 điểm)

a) Rút gọn biểu thức: \(A = \sqrt {27}  - \sqrt {12} \)  

b) Giải hệ phương trình \(\left\{ \begin{array}{l}7x - 3y = 5\\x + 3y = 3\end{array} \right.\)

Câu 2 (2 điểm)

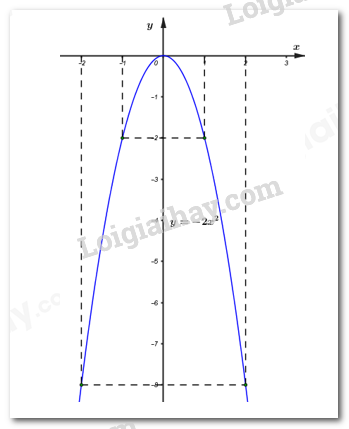
a) Trong mặt phẳng tọa độ \(\left( {Oxy} \right)\) cho parabol \(\left( P \right):\,\,y =  - 2{x^2}.\) Vẽ \(\left( P \right).\)

b) Tìm \(m\) để đường thẳng \(y = \left( {5m - 2} \right)x + 2019\) song song với đường thẳng \(y = x + 3.\)

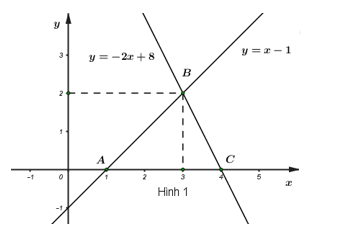
c) Hai đường thẳng \(y = x - 1\) và \(y =  - 2x + 8\) cắt nhau tại điểm \(B\) và lần lượt cắt trục \(Ox\) tại điểm \(A,\,\,C\) (hình 1). Xác định tọa độ các điểm \(A,\,\,B,\,\,C\) và tính diện tích tam giác \(ABC.\) 

Câu 3 (1,5 điểm):

a) Giải phương trình \({x^2} + 2x - 3 = 0.\)

b) Tìm \(m\) để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 7 = 0\) vô nghiệm.

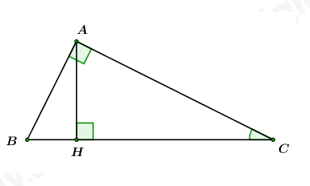
Câu 4 (1,5 điểm): Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,AC = 4cm.\) Tính độ dài đường cao \(AH,\) tính \(\cos \angle ACB\) và chu vi tam giác \(ABH.\)

Câu 5 (1,5 điểm)

a) Sau Kỳ thi tuyển sinh vào lớp 10 năm học 2019 – 2020, học sinh hia lớp 9A và 9B tặng lại thư viện trường 738 quyển sách gồm hai loại sách giáo khoa và sách tham khảo. Trong đó, mỗi học sinh lớp 9A tặng 6 quyển sách giáo khoa và 3 quyển sách tham khảo; mỗi học sinh lớp 9B tặng 5 quyển sách giáo khoa và 4 quyển sách tham khảo. Biết số sách giao khoa nhiều hơn số sách tham khảo là 166 quyển. Tính số học sinh của mỗi lớp.

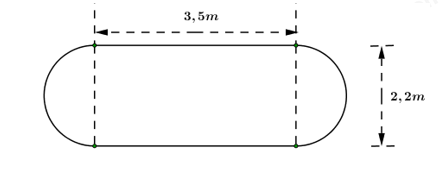
b) Một bồn chứa xăng đặt trên xe gồm hai nửa hình cầu có đường kính 2,2m và một hình trụ có chiều dài 3,5m (hình vẽ). Tính thể tích của bồn chứa xăng (kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy).

Câu 6 (2 điểm) : Cho tam giác \(ABC\) vuông cân tại \(A\), đường cao \(AH\,\,\left( {H \in BC} \right)\). Trên \(AC\) lấy điểm \(M\,\,\left( {M \ne A,\,\,M \ne C} \right)\) và vẽ đường tròn đường kính \(MC\). Kẻ \(BM\) cắt \(AH\) tại \(E\) và cắt đường tròn tại \(D\). Đường thẳng \(AD\) cắt đường tròn tại \(S\). Chứng minh rằng:

a) Tứ giác \(CDEH\) là tứ giác nội tiếp.

b) \(\angle BCA = \angle ACS\).

Lời giải

Câu 1: (1,5 điểm) (TH)

Phương pháp:

a) Sử dụng công thức khai căn: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A,\,\,khi\,\,A \ge 0\\ - A,\,\,khi\,\,\,A\, < 0\end{array} \right.\)

b) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.

Hướng dẫn giải:

a) Rút gọn biểu thức: \(A = \sqrt {27}  - \sqrt {12} \)  

Ta có: \(A = \sqrt {27}  - \sqrt {12}  = \sqrt {{3^2}.3}  - \sqrt {{2^2}.3}  = 3\sqrt 3  - 2\sqrt 3  = \sqrt 3 \)

b) Giải hệ phương trình \(\left\{ \begin{array}{l}7x - 3y = 5\\x + 3y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8x = 8\\x + 3y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = \dfrac{2}{3}\end{array} \right.\)

Vậy hệ phương trình có nghiệm là: \(\left( {x;y} \right) = \left( {1;\dfrac{2}{3}} \right)\)

Câu 2 (VD) (2 điểm):

Phương pháp:

a) Lập bảng giá trị các điểm mà đồ thị hàm số \(y =  - 2{x^2}\) đi qua rồi vẽ đồ thi hàm số.

b) Hai đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)

c) Dựa vào hình vẽ, xác định tọa độ các điểm \(A,\,\,B,\,\,C\) và tính diện tích tam giác \(ABC\) bằng công thức: \({S_{ABC}} = \dfrac{1}{2}BH.AC = \dfrac{1}{2}{y_B}.AC.\)

Cách giải:

a) Trong mặt phẳng tọa độ \(\left( {Oxy} \right)\) cho parabol \(\left( P \right):\,\,y =  - 2{x^2}.\) Vẽ \(\left( P \right).\)

Ta có bảng giá trị:

Vậy đồ thị hàm số \(\left( P \right):\,\,\,y =  - 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2; - 8} \right),\,\,\left( { - 1; - 2} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\, - 2} \right),\,\,\left( {2;\, - 8} \right).\)

Đồ thị hàm số \(\left( P \right):\,\,\,y =  - 2{x^2}\)

b) Tìm \(m\) để đường thẳng \(y = \left( {5m - 2} \right)x + 2019\) song song với đường thẳng \(y = x + 3.\)

Đường thẳng \(y = \left( {5m - 2} \right)x + 2019\) song song với đường thẳng \(y = x + 3\)

\( \Leftrightarrow \left\{ \begin{array}{l}5m - 2 = 1\\2019 \ne 3\,\,\left( {luon\,\,dung} \right)\end{array} \right. \Leftrightarrow 5m = 1 + 2 \Leftrightarrow m = \dfrac{3}{5}.\)

Vậy \(m = \dfrac{3}{5}\) thỏa mãn bài toán.

c) Hai đường thẳng \(y = x - 1\) và \(y =  - 2x + 8\) cắt nhau tại điểm \(B\) và lần lượt cắt trục \(Ox\) tại điểm \(A,\,\,C\) (hình 1). Xác định tọa độ các điểm \(A,\,\,B,\,\,C\) và tính diện tích tam giác \(ABC.\) 

Dựa vào Hình 1 ta thấy tọa độ các điểm \(A,\,\,B,\,\,C\) là: \(A\left( {1;\,\,0} \right),\,\,\,B\left( {3;\,\,2} \right),\,\,\,C\left( {4;\,\,0} \right).\)

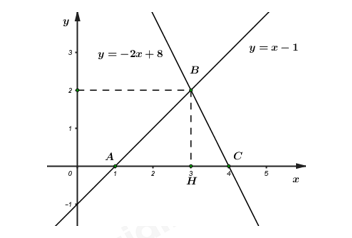
Gọi \(H\) là hình chiếu vuông góc của \(B\) trên \(AC,\,\) ta có: \({S_{ABC}} = \dfrac{1}{2}BH.AC.\)

Ta có: \(\left\{ \begin{array}{l}BH = {y_B} = 2\\AC = {x_C} - {x_A} = 4 - 1 = 3\end{array} \right. \Rightarrow {S_{ABC}} = \dfrac{1}{2}BH.AC = \dfrac{1}{2}.2.3 = 3\) (đvdt).

Câu 3 (VD) (1,5 điểm)

Phương pháp:

a) Giải phương trình bằng công thức nghiệm thu gọn hoặc nhẩm nghiệm.

b) Phương trình \(a{x^2} + bx + c = 0\,\,\,\left( {a \ne 0} \right)\) vô nghiệm \( \Leftrightarrow \Delta ' < 0.\)

Cách giải:

a) Giải phương trình \({x^2} + 2x - 3 = 0.\)

Phương trình:\({x^2} + 2x - 3 = 0\) có \(a = 1,\,\,b = 2,\,\,c =  - 3 \Rightarrow a + b + c = 1 + 2 - 3 = 0\)

\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \dfrac{c}{a} =  - 3\end{array} \right..\)

Vậy phương trình có tập nghiệm \(S = \left\{ {1;\,\, - 3} \right\}.\) 

b) Tìm \(m\) để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 7 = 0\) vô nghiệm.

Phương trình đã cho vô nghiệm \( \Leftrightarrow \Delta ' < 0\)

\(\begin{array}{l} \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} - 3m + 7 < 0\\ \Leftrightarrow {m^2} + 2m + 1 - {m^2} - 3m + 7 < 0\\ \Leftrightarrow  - m + 8 < 0 \Leftrightarrow m > 8.\end{array}\)

Vậy với \(m > 8\) thì phương trình đã cho vô nghiệm.

Câu 4 (VD) (1,5 điểm):

Phương pháp:

Sử dụng hệ thức lượng trong tam giác vuông và công thức tỉ số lượng giác để làm bài toán.

Cách giải:

Câu 5 (VD) (1,5 điểm):

Phương pháp:

a) Giải bài toán bằng cách lập hệ phương trình:

Gọi số học sinh lớp 9A là \(x\) (học sinh) \(\left( {x \in \mathbb{N}*} \right).\)

Gọi số học sinh lớp 9A là \(y\) (học sinh) \(\left( {y \in \mathbb{N}*} \right).\)

Biểu diễn số sách giáo khoa và sách tham khảo mỗi lớp tặng lại cho trường rồi lập hệ phương trình.

Giải hệ phương trình, đối chiếu với điều kiện của\(x,\,\,y\) rồi kết luận.

b) Thể tích của bồn chứa xăng = thể tích của khối cầu bán đường kính 2,2 m + thể tích của khối trụ có đường kính đáy là 2,2 m và chiều cao 3,5 m.

Cách giải:

a) Gọi số học sinh lớp 9A là \(x\) (học sinh) \(\left( {x \in {\mathbb{N}^*}} \right).\)

    Gọi số học sinh lớp 9B là \(y\) (học sinh) \(\left( {y \in {\mathbb{N}^*}} \right).\)

Số sách giáo khảo lớp 9A tặng cho trường là: \(6x\) (quyển sách).

Số sách tham khảo lớp 9A tặng cho trường là: \(3x\) (quyển sách).

Số sách giáo khảo lớp 9B tặng cho trường là: \(5y\) (quyển sách).

Số sách tham khảo lớp 9B tặng cho trường là: \(4y\) (quyển sách).

Tổng số sách cả hai lớp tặng cho trường là 738 quyển nên ta có phương trình:

\(6x + 3x + 5y + 4y = 738 \Leftrightarrow 9x + 9y = 738 \Leftrightarrow x + y = 82\,\,\,\left( 1 \right)\)

Tổng số sách giáo khoa nhiều hơn số sách tham khảo là 166 quyển nên ta có phương trình:

\(6x + 5y - \left( {3x + 4y} \right) = 166 \Leftrightarrow 3x + y = 166\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 82\\3x + y = 166\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 84\\y = 82 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 42\,\,\,\left( {tm} \right)\\y = 40\,\,\,\left( {tm} \right)\end{array} \right..\)

Vậy số lớp 9A có 42 học sinh, lớp 9B có 40 học sinh.

b) Bồn chứa xăng bao gồm 1 hình cầu và 1 hình trụ.

Ta có bán kính của hình cầu của bồn chứa xăng là: \(R = 2,\,2:2 = 1,1\,\,m.\)

\( \Rightarrow \) Thể tích phần hình cầu của bồn chứa xăng là: \({V_1} = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}.3,14.1,{1^3} \approx 5,57\,\,\left( {{m^3}} \right).\)

Phần hình trụ của bồn chứa xăng có bán kính đáy là: \(R = 1,1\,m\) và chiều cao là: \(h = 3,5\,m.\)

\( \Rightarrow \) Thể tích phần hình trụ của bồn chứa xăng là: \({V_2} = \pi {R^2}h = 3,14.1,{1^2}.3,5 = 13,3\,\,\,\left( {{m^3}} \right).\)

Vậy thể tích của bồn chứa xăng là: \(V = {V_1} + {V_2} = 5,57 + 13,3 = 18,87\,\,\,\left( {{m^3}} \right).\)

Câu 6 (VD):

Cách giải:

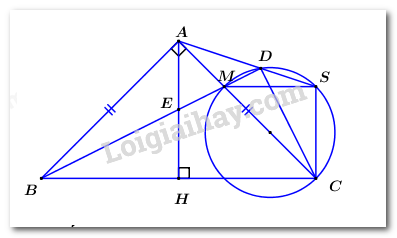
a) Tứ giác \(CDEH\) là tứ giác nội tiếp.

Ta có : \(\angle EHC = {90^0}\) (\(AH\) là đường cao của \(\Delta ABC\))

Ta có \(\angle CDM = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính \(MC\)).

\( \Rightarrow \angle CDE = {90^0}\).

Xét tứ giác \(CDEH\) có : \(\angle CDE + \angle CHE = {90^0} + {90^0} = {180^0}\), suy ra tứ giác \(CDEH\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).

b) \(\angle BCA = \angle ACS\).

Ta có \(\angle CDE = {90^0}\,\,\left( {cmt} \right) \Rightarrow \angle CDB = {90^0}\).

Xét tứ giác \(ADCB\) có : \(\angle CDB = \angle CAB = {90^0} \Rightarrow \) Tứ giác \(ADCB\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau).

\( \Rightarrow \angle BDA = \angle BCA\) (hai góc nội tiếp cùng chắn cung \(AB\)).

Tứ giác \(CSDM\) nội tiếp đường tròn đường kính \(CM \Rightarrow \angle MCS = \angle ADM = \angle BDA\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).

\( \Rightarrow \angle BCA = \angle MCS = \angle ACS\,\,\left( {dpcm} \right)\).

Từ (1) và (2) suy ra

\( \Rightarrow \angle AFE + \angle BAA' = \angle ACB + \angle BCA'\)

Mà \(\angle ACB + \angle BCA' = \angle A'CA = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

Nên \(\angle AFE + \angle BAA' = {90^0}\) hay \(\angle AFI + \angle FAI = {90^0}\)

\( \Rightarrow \angle AIF = {90^0}\) \( \Rightarrow AO \bot PG\) tại \(I\)

\( \Rightarrow I\) là trung điểm của \(PG\) (đường kính vuông góc với dây thì đi qua trung điểm của dây ấy)

\( \Rightarrow AO\) là đường trung trực của \(PG\). (đpcm)