Đề thi vào 10 môn Toán Bến Tre năm 2023
Phần I: Trắc nghiệm (4 điểm) Câu 1: Giá trị của biểu thức \(\sqrt 9 {\rm{ \;}} - 2\) bằng A. 1 B. 7 C. \( - 5\) D. 79
Đề bài
Phần I: Trắc nghiệm (4 điểm)
Câu 1: Giá trị của biểu thức \(\sqrt 9 {\rm{ \;}} - 2\) bằng
A. 1
B. 7
C. \( - 5\)
D. 79
Câu 2: Điều kiện của \(x\) để biểu thức \(\sqrt {2x - 8} \) có nghĩa là
A. \(x = 4\).
B. \(x > 4\).
C. \(x < 4\).
D. \(x \ge 4\).
Câu 3: Kết quả rút gọn của biểu thức \(M = \sqrt {9x{y^2}} \) với \(x \ge 0,y < 0\) bằng
A. \(M = {\rm{ \;}} - 3y\sqrt x \).
B. \(M = 3y\sqrt x \).
C. \(M = {\rm{ \;}} - 3xy\).
D. \(M = 3\sqrt {xy} \).
Câu 4: Hàm số \(y = {x^2}\) có đồ thị là hình vẽ nào dưới đây?
A. 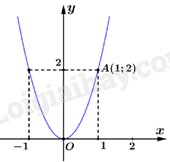
B. 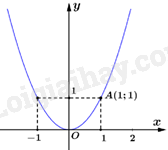
C. 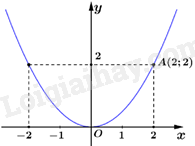
D. 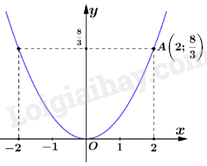
Câu 5: Điểm nào sau đây thuộc đường thẳng \(y = 7x - 6\) ?
A. \(M\left( {0;1} \right)\).
B. \(N\left( {2;4} \right)\).
C. \(P\left( {1;1} \right)\).
D. \(Q\left( {2;2} \right)\).
Câu 6: Tọa độ các giao điểm của đường thẳng \(y = 7x\) và parabol \(y = {\rm{ \;}} - {x^2}\) là
A. \(M\left( {0;1} \right),N\left( {7;14} \right)\).
B. \(M\left( {1;0} \right),N\left( {7;49} \right)\).
C. \(M\left( {0;0} \right),N\left( { - 7; - 49} \right)\)
D. \(M\left( {1;1} \right),N\left( { - 7;49} \right)\).
Câu 7: Hàm số \(y = 3{x^2}\) nghịch biến khi
A. \(x > 0\).
B. \(x < 0\).
C. \(x > 1\).
D. \(x \ne 0\).
Câu 8: Tìm tham số \(m\) để đường thẳng \(y = 3x + 2m - 7\) đi qua điểm \(M\left( { - 2;4} \right)\) ?
A. \(m = {\rm{ \;}} - \frac{7}{2}\).
B. \(m = 9\).
C. \(m = {\rm{ \;}} - \frac{{17}}{2}\).
D. \(m = \frac{{17}}{2}\).
Câu 9: Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
A. \(y = 3x - 2\)
B. \(y = 2{x^2}\).
C. \(y = \frac{1}{x}\).
D. \(y = 7\sqrt x \).
Câu 10: Tính biệt thức \(\Delta \) của phương trình: \({x^2} + 2mx - 9 = 0\) với \(m\) là tham số.
A. \(\Delta = 40\).
B. \(\Delta = 36m\).
C. \(\Delta = 4{m^2} + 36\).
D. \(\Delta = {m^2} + 9\).
Câu 11: Phương trình: \(5{x^2} + 2x = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Khi đó \({x_1} + {x_2}\) bằng
A. \(\frac{2}{5}\).
B. \( - \frac{2}{5}\).
C. \( - \frac{1}{5}\).
D. 0 .
Câu 12: Một nghiệm của phương trình: \(3{x^4} - \left( {2 + \sqrt 3 } \right){x^2} - 1 + \sqrt 3 {\rm{ \;}} = 0\)
A. \(x = {\rm{ \;}} - 2\).
B. \(x = {\rm{ \;}} - 3\).
C. \(x = 2\).
D. \(x = {\rm{ \;}} - 1\).
Câu 13: Cho tam giác ABC vuông tại \(A\) có \(AB = 4\;{\rm{cm}}\) và \(AC = 5\;{\rm{cm}}\). Khi đó độ dài của đoạn thẳng BC bằng
A. \(BC = 6\;{\rm{cm}}\).
B. \(BC = \sqrt {41} \;{\rm{cm}}\).
C. \(BC = 3\;{\rm{cm}}\).
D. \(BC = 41\;{\rm{cm}}\).
Câu 14: Cho đường tròn \(\left( {O;4\;{\rm{cm}}} \right)\), đường kính của \((O)\) có độ dài bằng
A. \(8\;{\rm{cm}}\).
B. \(4\;{\rm{cm}}\).
C. \(2\;{\rm{cm}}\).
D. \(1\;{\rm{cm}}\).
Câu 15: Cho tam giác ABD nội tiếp đường tròn \((O)\) và \(\widehat {AOB} = 60^\circ \) (tham khảo hình vẽ bên). Số đo của góc bằng
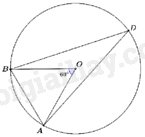
A. \(60^\circ \).
B. \(120^\circ \).
C. \(30^\circ \).
D. \(90^\circ \).
Câu 16: Cho tam giác ABC vuông tại \(A\) biết \(\widehat {ABC} = 30^\circ \) và \(AC = 7\;{\rm{cm}}\) (tham khảo hình vẽ bên). Độ dài của đoạn thẳng AB
A. \(3\sqrt 3 \;{\rm{cm}}\).
B. \(\sqrt 3 \;{\rm{cm}}\).
C. \(\frac{{7\sqrt 3 }}{3}\;{\rm{cm}}\).
D. \(7\sqrt 3 \;{\rm{cm}}\).
Câu 17: Một hình trụ có chiều cao \(h = 10\;{\rm{cm}}\) và đường kính của đường tròn đáy bằng \(6\;{\rm{cm}}\). Diện tích xung quanh của hình trụ đó bằng
A. \(30\pi {\rm{c}}{{\rm{m}}^2}\).
B. \(15\pi {\rm{c}}{{\rm{m}}^2}\).
C. \(60\pi {\rm{c}}{{\rm{m}}^2}\).
D. \(90\pi {\rm{c}}{{\rm{m}}^2}\).
Câu 18: Cho tam giác BCD nội tiếp đường tròn tâm \(O\) và \(\angle CBD = 60^\circ \). Dựng tiếp tuyến Dx của đường tròn \(\left( O \right)\) như hình vẽ. Khi đó, số đo của góc CDx
A. \(120^\circ \).
B. \(60^\circ \).
C. \(30^\circ \).
D. \(100^\circ \).
Câu 19: Diện tích mặt cầu có đường kính \(30\;{\rm{cm}}\) bằng
A. \(300\pi {\rm{c}}{{\rm{m}}^2}\).
B. \(1200\pi {\rm{c}}{{\rm{m}}^2}\).
C. \(3600\pi {\rm{c}}{{\rm{m}}^2}\).
D. \(900\pi {\rm{c}}{{\rm{m}}^2}\).
Câu 20: Cho \(\Delta ABC\) vuông tại \(B\) có đường cao BD, biết \(AD = 4\;{\rm{cm}},DC = 8\;{\rm{cm}}\) (tham khảo hình vẽ bên). Độ dài đoạn thẳng AB
A. \(\sqrt 3 \;{\rm{cm}}\)
B. \(4\sqrt 3 \;{\rm{cm}}\)
C. \(32\;{\rm{cm}}\)
D. \(4\sqrt 2 \;{\rm{cm}}\)
Phần II. Tự luận (6 điểm)
Câu 21: Vẽ đồ thị của hàm số \(y = 2{x^2}\).
Câu 22: Giải phương trình: \(3{x^2} + 4x - 9 = 0\).
Câu 23: Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 3}\\{2x - 3y = {\rm{ \;}} - 4}\end{array}} \right.\).
Câu 24: Rút gọn biểu thức: \(A = \frac{{x - \sqrt x }}{{\sqrt x {\rm{ \;}} - 1}}:\frac{1}{{\sqrt x }}\) với \(x > 0\) và \(x \ne 1\).
Câu 25: Tìm các giá trị của tham số \(m\) để phương trình: \({x^2} - \left( {m + 1} \right)x - 2023 = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa: \(\frac{1}{{{x_1} - 2023}} + \frac{1}{{{x_2} - 2023}} = 1\).
Câu 26: Cho các số thực a, b thỏa mãn: \({a^2} + {b^2} - 14a + 12b + 85 = 0\). Tính giá trị của biểu thức: \(B = 3a + 2b\)
Câu 27: Để chuẩn bị tham gia kỳ thi tuyển sinh vào lớp 10 đạt kết quả như mong đợi, bạn A đã lập kế hoạch sẽ làm xong 80 bài tập trong khoảng thời gian nhất định với số lượng bài tâp được chia đều trong các ngày. Trên thực tế, khi làm bài tập, mỗi ngày bạn A đã làm thêm 2 bài tập so với kế hoạch ban đầu nên đã hoàn thành kế hoạch sớm hơn 2 ngày so với dự định. Hỏi theo kế hoạch, mỗi ngày bạn A phải làm xong bao nhiêu bài tập?
Câu 28: Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Kẻ AH vuông góc với BC tại H, kẻ HE vuông góc với AB tại E, kẻ HD vuông góc với AC tại D.
a) Chứng minh: tứ giác AEHD là tứ giác nội tiếp.
b) Dựng đường kính AK của đường tròn (O). Chứng minh: AE.AK = AH.AC.
-----HẾT-----
Lời giải chi tiết
Phần I: Trắc nghiệm
Câu 1 (NB):
Phương pháp:
Tính toán với căn bậc hai \(\sqrt {{a^2}} {\rm{ \;}} = \left| a \right|\)
Cách giải:
\(\sqrt 9 {\rm{ \;}} - 2 = 3 - 2 = 1\)
Chọn A.
Câu 2 (NB):
Phương pháp:
\(\sqrt {f(x)} \) có nghĩa khi \(f(x) \ge 0\)
Cách giải:
\(\sqrt {2x - 8} \) có nghĩa khi \(2x - 8 \ge 0 \Leftrightarrow x \ge 4\)
Chọn D.
Câu 3 (TH):
Phương pháp:
Hằng đẳng thức \(\sqrt {{A^2}} {\rm{ \;}} = \left| A \right|\)
Cách giải:
Với \(x \ge 0,y < 0\) thì \(M = \sqrt {9x{y^2}} {\rm{ \;}} = \sqrt {{{(3y)}^2}x} {\rm{ \;}} = \left| {3y} \right|\sqrt x {\rm{ \;}} = {\rm{ \;}} - 3y\sqrt x \)
Chọn A.
Câu 4 (NB):
Phương pháp:
Đồ thị hàm số \(y = a{x^2}(a \ne 0)\) đi qua điểm \(M({x_0};{y_0})\) thỏa mãn \({y_0} = a{x_0}^2\)
Cách giải:
Thay tọa độ điểm \(A(1;1)\) vào hàm số \(y = {x^2}\) ta được: \(1 = {1^2}\) (luôn đúng)
Suy ra đồ thị hàm số \(y = {x^2}\) đi qua điểm \(A(1;1)\)
Chọn B.
Câu 5 (NB):
Phương pháp:
Đường thẳng \(y = ax + b(a \ne 0)\) đi qua điểm \(M({x_0};{y_0})\) thỏa mãn \({y_0} = a{x_0} + b\)
Cách giải:
Thay tọa độ điểm \(P\left( {1;1} \right)\) vào đường thẳng \(y = 7x - 6\) ta được: \(1 = 7.1 - 6 = 1\) (luôn đúng)
Vậy điểm \(P\left( {1;1} \right)\) thuộc đường thẳng \(y = 7x - 6\)
Chọn C.
Câu 6 (TH):
Phương pháp:
Xét phương trình hoành độ giao điểm của (P) và (d).
Cách giải:
Xét phương trình hoành độ giao điểm của (P) và (d) ta được:
\(\begin{array}{*{20}{l}}{7x = {\rm{ \;}} - {x^2}}\\{ \Leftrightarrow {x^2} + 7x = 0}\\{ \Leftrightarrow x(x + 7) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0 \Rightarrow y = 0}\\{x = {\rm{ \;}} - 7 \Rightarrow y = 7.( - 7) = {\rm{ \;}} - 49}\end{array}} \right.}\end{array}\)
Vạy (P) và (d) cắt nhau tại hai điểm \((0;0),( - 7; - 49)\)
Chọn C.
Câu 7 (NB):
Phương pháp:
Hàm số \(y = a{x^2}(a \ne 0)\) nghịch biến khi \(\left\{ {\begin{array}{*{20}{l}}{a > 0}\\{x < 0}\end{array}} \right.\) hoặc \(\left\{ {\begin{array}{*{20}{l}}{a < 0}\\{x > 0}\end{array}} \right.\)
Cách giải:
Hàm số \(y = 3{x^2}\) nghịch biến khi \(\left\{ {\begin{array}{*{20}{l}}{3 > 0}\\{x < 0}\end{array}} \right.\)
Chọn B.
Câu 8 (NB):
Phương pháp:
Đường thẳng \(y = ax + b(a \ne 0)\) đi qua điểm \(M({x_0};{y_0})\) thỏa mãn \({y_0} = a{x_0} + b\)
Cách giải:
Thay tọa độ điểm \(M\left( { - 2;4} \right)\) vào \(y = 3x + 2m - 7\) ta được:
\(\begin{array}{*{20}{l}}{4 = 3.( - 2) + 2m - 7}\\{ \Leftrightarrow 2m = 4 + 6 + 7}\\{ \Leftrightarrow 2m = 17}\\{ \Leftrightarrow m = \frac{{17}}{2}}\end{array}\)
Chọn D.
Câu 9 (NB):
Phương pháp:
Hàm số bậc nhất có dạng \(y = ax + b(a \ne 0)\) với a, b là hệ số.
Cách giải:
Hàm số \(y = 3x - 2\) là hàm số bậc nhất.
Chọn A.
Câu 10 (NB):
Phương pháp:
Công thức \(\Delta {\rm{ \;}} = {b^2} - 4ac\)
Cách giải:
Phương trình: \({x^2} + 2mx - 9 = 0\) có: \(\Delta {\rm{ \;}} = {(2m)^2} - 4.( - 9) = 4{m^2} + 36\)
Chọn C.
Câu 11 (NB):
Phương pháp:
Hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
Phương trình: \(5{x^2} + 2x = 0\) có \({x_1} + {x_2} = \frac{{ - 2}}{5}\)
Chọn B.
Câu 12 (TH):
Phương pháp:
Đưa phương trình về dạng \(a{x^2} + bx + c = 0(a \ne 0)\), nhẩm nghiệm:
Nếu \(a + b + c = 0\) thì phương trình có nghiệm \(\left[ {\begin{array}{*{20}{l}}{{x_1} = 1}\\{{x_2} = \frac{c}{a}}\end{array}} \right.\)
Nếu \(a - b + c = 0\) thì phương trình có nghiệm \(\left[ {\begin{array}{*{20}{l}}{{x_1} = {\rm{ \;}} - 1}\\{{x_2} = \frac{{ - c}}{a}}\end{array}} \right.\)
Cách giải:
Phương trình \(3{x^4} - \left( {2 + \sqrt 3 } \right){x^2} - 1 + \sqrt 3 {\rm{ \;}} = 0\)
Đặt \({x^2} = t(t \ge 0) \Rightarrow 3{t^2} - \left( {2 + \sqrt 3 } \right){t^2} - 1 + \sqrt 3 {\rm{ \;}} = 0\)
Có \(a + b + c = 3 - 2 - \sqrt 3 {\rm{ \;}} - 1 + \sqrt 3 {\rm{ \;}} = 0\) \( \Rightarrow \) Phương trình có nghiệm \(\left[ {\begin{array}{*{20}{l}}{{t_1} = 1 \Rightarrow {x^2} = 1 \Rightarrow x = {\rm{ \;}} \pm 1}\\{{t_2} = \frac{{ - 1 + \sqrt 3 }}{3}}\end{array}} \right.\)
Vậy một nghiệm của phương trình là \(x = {\rm{ \;}} - 1\)
Chọn D.
Câu 13 (NB):
Phương pháp:
Áp dụng định lí Pytago vào \(\Delta ABC\) vuông tại A có: \(B{C^2} = A{B^2} + A{C^2}\)
Cách giải:
Áp dụng định lí Pytago vào \(\Delta ABC\) vuông tại A có: \(B{C^2} = A{B^2} + A{C^2} \Rightarrow BC = \sqrt {{4^2} + {5^2}} {\rm{ \;}} = \sqrt {41} (cm)\)
Chọn B.
Câu 14 (NB):
Phương pháp:
Đường tròn \((O;R)\) có bán kính \(R\), đường kính 2R
Cách giải:
Đường tròn \(\left( {O;4\;{\rm{cm}}} \right)\) có đường kính bằng \(2.4 = 8\)cm
Chọn A.
Câu 15 (NB):
Phương pháp:
Góc nội tiếp bằng một nửa số đo góc ở tâm cùng chắn một cung.
Cách giải:
Xét (O) có: \(\angle ADB = \frac{1}{2}\angle AOB = \frac{1}{2}.60^\circ {\rm{ \;}} = 30^\circ \) (tính chất góc nội tiếp và góc ở tâm cùng chắn cung AB)
Chọn C.
Câu 16 (NB):
Phương pháp:
Công thức lượng giác \(\Delta ABC\) vuông tại \(A\) có \(\tan B = \frac{{AC}}{{AB}}\)
Cách giải:
\(\Delta ABC\) vuông tại \(A\) có \(\tan B = \frac{{AC}}{{AB}}\) \( \Rightarrow \tan 30^\circ {\rm{\;}} = \frac{7}{{AB}} \Leftrightarrow \frac{{\sqrt 3 }}{3} = \frac{7}{{AB}} \Rightarrow AB = \frac{{3.7}}{{\sqrt 3 }} = 7\sqrt 3 \)
Chọn D.
Câu 17 (NB):
Phương pháp:
Diện tích xung quanh của hình lăng trụ \({S_{xq}} = 2\pi R.h\) với \(h\) là chiều cao, \(R\) là bán kính.
Cách giải:
Một hình trụ có chiều cao \(h = 10\;{\rm{cm}}\) và đường kính của đường tròn đáy bằng \(6\;{\rm{cm}}\)
Tức là \(2R = 6(cm)\)
Diện tích xung quanh hình trụ là \(2\pi R.h = 6.10\pi {\rm{ \;}} = 60\pi (c{m^2})\)
Chọn C.
Câu 18 (TH):
Phương pháp:
Tam giác ABC nội tiếp đường tròn (O), nên tam giác ABC đều.
Tính chất góc nội tiếp bằng góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung.
Cách giải:
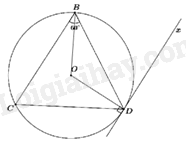
Vì tam giác ABC nội tiếp đường tròn (O), nên tam giác ABC đều.
\( \Rightarrow \angle BCD = \angle CDB = 60^\circ \)
Xét (O) có: \(\angle BDx = \angle BCD = 60^\circ \) (góc nội tiếp bằng góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BD)
\( \Rightarrow \angle CDx = \angle CDB + \angle BDx = 60^\circ {\rm{ \;}} + 60^\circ {\rm{ \;}} = 120^\circ \)
Chọn A.
Câu 19 (NB):
Phương pháp:
Diện tích mặt cầu \(S = 4\pi {R^2}\)
Cách giải:
Diện tích mặt cầu có đường kính \(30\;{\rm{cm}}\) bằng: \(S = 4\pi {R^2} = 4\pi .{\left( {\frac{{30}}{2}} \right)^2} = 900\pi (c{m^2})\)
Chọn D.
Câu 20 (NB):
Phương pháp:
Hệ thức lượng trong \(\Delta ABC\) vuông tại \(B\) có đường cao BD: \(A{B^2} = AD.AC\)
Cách giải:
Hệ thức lượng trong \(\Delta ABC\) vuông tại \(B\) có đường cao BD: \(A{B^2} = AD.AC \Rightarrow AB = \sqrt {4.(4 + 8)} {\rm{ \;}} = 4\sqrt 3 cm\)
Chọn B.
Phần II: Tự luận
Câu 21 (NB):
Phương pháp:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị tương ứng giữa \(x\) và \(y\).
Bước 3: Vẽ đồ thị và kết luận.
Chú ý: vì đồ thị hàm số \(y = a{x^2}(a \ne 0)\) luôn đi qua gốc tọa độ \(O\) và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này , ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng
qua Oy.
Cách giải:
Tập xác định: \(x \in \mathbb{R}\).
Bảng giá trị:

Ta thấy \(a = 2 > 0\) nên đồ thị có bề lõm hướng xuống dưới và đi qua 5 điểm \(A\left( { - 2;8} \right)\); \(B\left( { - 1;2} \right)\); \(O\left( {0;0} \right)\); \(C\left( {1;2} \right)\); \(D\left( {2;8} \right)\).
Đồ thị \(y = 2{x^2}\) là một Parabol có bề lõm hướng lên, nằm phía trên Ox, nhận Oy làm trục đối xứng và đi qua các điểm \(A\left( { - 2;8} \right)\); \(B\left( { - 1;2} \right)\); \(O\left( {0;0} \right)\); \(C\left( {1;2} \right)\); \(D\left( {2;8} \right)\).
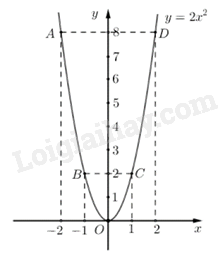
Câu 22 (NB):
Phương pháp:
Công thức \(\Delta ' = {(b')^2} - ac\) với \(b' = \frac{b}{2}\)
Nếu \(\Delta ' > 0 \Rightarrow \) PT có hai nghiệm \(x = \frac{{ - b' \pm \sqrt {\Delta '} }}{a}\)
Nếu \(\Delta {\rm{ \;}} = 0 \Rightarrow \) PT có nghiệm kép \(x = \frac{{ - b'}}{a}\)
Nếu \(\Delta {\rm{ \;}} < 0 \Rightarrow \) PT vô nghiệm
Cách giải:
Xét phương trình \(3{x^2} + 4x - 9 = 0\) có: \(\Delta ' = {2^2} - 3.\left( { - 9} \right) = 4 - \left( { - 27} \right) = 31 > 0\)
Suy ra phương trình có hai nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - 2 - \sqrt {31} }}{3}}\\{{x_2} = \frac{{ - 2 + \sqrt {31} }}{3}}\end{array}} \right.\)
Vậy phương trình có hai nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - 2 - \sqrt {31} }}{3}}\\{{x_2} = \frac{{ - 2 + \sqrt {31} }}{3}}\end{array}} \right.\).
Câu 23 (NB):
Phương pháp:
Giải hệ bằng phương pháp cộng đại số.
Cách giải:
Hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x + y = 3}\\{2x - 3y = {\rm{ \;}} - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + 2y = 6}\\{2x - 3y = {\rm{ \;}} - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{5y = 10}\\{x = 3 - y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 2}\\{x = 1}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {1;2} \right)\).
Câu 24 (TH):
Phương pháp:
Rút gọn biểu thức thông qua: quy đồng, tính toán, đổi dấu.
Cách giải:
\(\begin{array}{*{20}{l}}{A = \frac{{x - \sqrt x }}{{\sqrt x {\rm{ \;}} - 1}}:\frac{1}{{\sqrt x }}}\\{A = \frac{{\sqrt x \left( {\sqrt x {\rm{ \;}} - 1} \right)}}{{\sqrt x {\rm{ \;}} - 1}}:\frac{1}{{\sqrt x }}}\\{A = \sqrt x :\frac{1}{{\sqrt x }}}\\{A = \sqrt x \sqrt x {\rm{ \;}} = x.}\end{array}\)
Vậy \(A = x.\) với \(x > 0\) và \(x \ne 1\).
Câu 25 (TH):
Phương pháp:
Công thức \(\Delta {\rm{ \;}} = {b^2} - 4ac\)
Điều kiện \(\Delta {\rm{ \;}} > 0\) để PT có hai nghiệm phân biệt
Hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
Xét phương trình \({x^2} - (m + 1)x - 2023 = 0\) có \(\Delta {\rm{ \;}} = {\left[ { - \left( {m + 1} \right)} \right]^2} - 4.1.\left( { - 2023} \right) = {\left( {m + 1} \right)^2} + 8092 > 0\) với mọi m.
Vậy phương trình luôn có hai nghiệm phân biệt \({x_1},{x_2}\) với mọi m
Áp dụng định lí Vi – ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = m + 1}\\{{x_1}.{x_2} = {\rm{ \;}} - 2023}\end{array}} \right.\) (1)
Ta có \(\frac{1}{{{x_1} - 2023}} + \frac{1}{{{x_2} - 2023}} = 1\)
\(\begin{array}{l} \Leftrightarrow \frac{{{x_2} - 2023}}{{\left( {{x_1} - 2023} \right)\left( {{x_2} - 2023} \right)}} + \frac{{{x_1} - 2023}}{{\left( {{x_1} - 2023} \right)\left( {{x_2} - 2023} \right)}} = 1\\ \Leftrightarrow \frac{{{x_2} - 2023 + {x_1} - 2023}}{{\left( {{x_1} - 2023} \right)\left( {{x_2} - 2023} \right)}} = 1\\ \Leftrightarrow {x_1} + {x_2} - 4046 = \,\,{x_1}{x_2} - 2023\left( {{x_1} + {x_2}} \right) + {2023^2}\,\,\,\\\,\, \Leftrightarrow \,{x_1}{x_2} - 2024\left( {{x_1} + {x_2}} \right) + {2023^2} + 4046 = 0 & & \left( 2 \right)\end{array}\)
Thay (1) vào (2) ta có:
\(\begin{array}{l} - 2023 - 2024.\left( {m + 1} \right) + {2023^2} + 4026 = 0\\ \Leftrightarrow - 2024\left( {m + 1} \right) = - 4094552\\ \Leftrightarrow m + 1 = 2023\\ \Leftrightarrow m = 2022\left( {TM} \right)\end{array}\)
Vậy m = 2022
Câu 26 (VD):
Phương pháp:
Biến đổi biểu thức về dạng \({(a + b)^2} + {(c + d)^2} = 0\) \( \Leftrightarrow \left\{ \begin{array}{l}{(a + b)^2} = 0\\{(c + d)^2} = 0\end{array} \right.\) vì \({A^2} \ge 0,\forall A\)
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {a^2} + {b^2} - 14a + 12b + 85 = 0}\\{ \Leftrightarrow {a^2} - 14a + 49 + {b^2} + 12b + 36 = 0}\\{ \Leftrightarrow {{(a - 7)}^2} + {{(b + 6)}^2} = 0}\end{array}\)
Vì \({(a - 7)^2} \ge 0\quad \forall a \in \mathbb{R}\); \({(b + 6)^2} \ge 0\quad \forall b \in \mathbb{R}\)
Suy ra: \(\left\{ {\begin{array}{*{20}{l}}{a - 7 = 0}\\{b + 6 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 7}\\{b = {\rm{ \;}} - 6}\end{array}} \right.\)
Do đó: \(B = 3a + 2b = 3.7 + 2.\left( { - 6} \right) = 21 - 12 = 9\)
Vậy \(B = 9.\)
Câu 27 (TH):
Phương pháp:
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
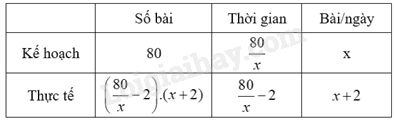
PT: thực tế bạn A đã hoàn thành 80 bài theo kế hoạch.
Cách giải:
Gọi số bài tập mỗi ngày bạn A phải làm theo kế hoạch ban đầu là \(x\) (bài). (Điều kiện \(x \in \mathbb{N},0 < x < 80\))
Như vậy theo kế hoạch, số ngày để bạn An hoàn thành 80 bài tập là: \(\frac{{80}}{x}\) (ngày)
Vì thực tế mỗi ngày bạn A làm thêm 2 bài tập so với kế hoạch nên mỗi ngày A làm được \(x + 2\) bài
Do A hoàn thành sớm hơn 2 ngày so với dự định nên ta có phương trình:
\(\left( {x + 2} \right)\left( {\frac{{80}}{x} - 2} \right) = 80\)
\(\begin{array}{l} \Rightarrow \left( {x + 2} \right)\left( {80 - 2x} \right) = 80x\\ \Leftrightarrow 80x - 2{x^2} - 4x + 160 = 80x\\ \Leftrightarrow 2{x^2} + 4x - 160 = 0\\ \Leftrightarrow {x^2} + 2x - 80 = 0\\ \Leftrightarrow {x^2} + 10x - 8x - 80 = 0\\ \Leftrightarrow x\left( {x + 10} \right) - 8\left( {x + 10} \right) = 0\\ \Leftrightarrow \left( {x - 8} \right)\left( {x + 10} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 8 = 0\\x + 10 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 8\,\,(TM)\\x = - 10\,\,(KTM)\end{array} \right.\end{array}\)
Vậy theo kế hoạch, mỗi ngày bạn A phải làm xong 8 bài tập.
Câu 28 (VD):
Phương pháp:
a) Chứng minh AEHD có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Áp dụng hệ thức lượng trong tam giác vuông \(\Delta AHC\) và \(\Delta AHB\) chứng minh được \(AE.AB = AD.AC\) suy ra $\Delta AED\backsim \Delta ACB\left( c.g.c \right)$
Áp dụng thêm tính chất góc nội tiếp cùng chắn một cung bằng nhau.
Chứng minh $\Delta AEH\backsim \Delta ACK\left( g.g \right)$ suy ra cạnh tương ứng tỉ lệ.
Cách giải:
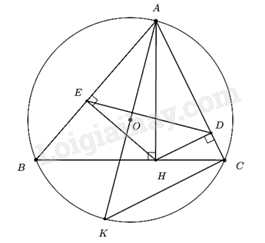
a) Xét tứ giác AEHD có:
\(\angle AEH = {90^0}\) (\(HE \bot AB\))
\(\angle ADH = {90^0}\) (\(HD \bot AC\))
\( \Rightarrow \)\(\angle AEH + \angle ADH = {90^0} + {90^0} = {180^0}\)
Suy ra tứ giác AEHD nội tiếp (tổng hai góc đối bằng \({180^0}\)) (dhnb)
b) Xét \(\Delta AHB\) vuông tại H, đường cao HE có:
\(A{H^2} = AE.AB\) (hệ thức lượng trong tam giác vuông)
Xét \(\Delta AHC\) vuông tại H, đường cao HE có:
\(A{H^2} = AD.AC\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow AE.AB = AD.AC \Leftrightarrow \frac{{AE}}{{AC}} = \frac{{AD}}{{AB}}\)
Xét \(\Delta AED\) và \(\Delta ABC\) có \(\angle BAC\) chung và \(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}}\) (cmt)
$\Rightarrow \Delta AED \backsim \Delta ACB\left( {c.g.c} \right) \Rightarrow \angle ADE = \angle ABC$ (2 góc tương ứng)
Mà \(\angle ABC = \angle AKC\) (cùng chắn cung AC)
\( \Rightarrow \angle ADE = \angle AKC\left( { = \angle ABC} \right)\)
Do AEHD nội tiếp nên \(\angle AHE = \angle ADE\) (cùng chắn cung AE)
\( \Rightarrow \angle AHE = \angle AKC\)
Xét \(\Delta AEH\) và \(\Delta ACK\) có
\(\angle AHE = \angle AKC\)
\(\angle AEH = \angle ACK = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
$\Rightarrow \Delta AEH \backsim \Delta ACK\left( {g.g} \right) \Rightarrow \dfrac{{AE}}{{AC}} = \dfrac{{AH}}{{AK}} \Rightarrow AE.AK = AH.AC$ (đpcm)
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi vào 10 môn Toán Bến Tre năm 2023 timdapan.com"







