Đề thi học kì 2 môn toán lớp 8 năm 2019 - 2020 trường THCS Nghĩa Tân

Đề bài

Bài 1  (2,0 điểm):

Cho hai biểu thức: \(A = \dfrac{{x - 2}}{x}\)  và \(B = \dfrac{{4x}}{{x + 1}} + \dfrac{x}{{1 - x}} + \dfrac{{2x}}{{{x^2} - 1}}\)  với \(x \ne  \pm 1;x \ne 0\)

a) Tính giá trị của biểu thức A khi \(x = \dfrac{2}{3}\)

b) Chứng minh rằng: \(B = \dfrac{{3x}}{{x + 1}}\)

c) Cho \(P = A.B.\) Tìm tất cả các giá trị của \(m\) để phương trình \(P = m\) có nghiệm duy nhất.

Bài 2 (2,0 điểm):

Một người đi xe máy từ A đến B với vận tốc \(50\) km/h, sau đó 30 phút, một ôtô cũng xuất phát từ A đến B với vận tốc 60 km/h. Tính độ dài quãng đường AB biết cả 2 xe đến B cùng lúc.

Bài 3 (2,5 điểm):

Giải các phương trình và bất phương trình sau:

a) \(3x\left( {x - 2} \right) = {x^2} - 4\)

b) \(\dfrac{{x + 3}}{{x - 1}} + \dfrac{x}{{x + 1}} = \dfrac{{{x^2} + 4x + 5}}{{{x^2} - 1}}\)

c) \(3\left( {x - 1} \right) < 5\left( {x + 1} \right) - 2\)

d) \({x^3} >  - 2x\)

Bài 4 (3 điểm): Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), đường cao AH

a) Chứng minh rằng \(\Delta BHA \backsim \Delta BAC\). Từ đó suy ra \(B{A^2} = BH.BC\)

b) Lấy điểm I thuộc AH. Kẻ đường thẳng đi qua B và vuông góc với CI tại K. Chứng minh rằng \(CH.CB = CI.CK\)

c) Tia BK cắt tia HA tại D. Chứng minh rằng \(\widehat {BHK} = \widehat {BDC}\)

d) Trên tia đối của tia KC lấy điểm M sao cho \(BM = BA.\) Chứng minh rằng \(\widehat {BMD} = {90^0}\) . 

Bài 5 (0,5 điểm):

Cho \(x > 0.\) Tìm giá trị nhỏ nhất của biểu thức:

\(M = 4{x^2} - 3x + \dfrac{1}{{4x}} + 2020\)

---

LG bài 1

Phương pháp giải:

a) Thay \(x = \dfrac{2}{3}\)  vào biểu thức A rồi tính toán

b) Qui đồng rồi thực hiện cộng trừ các phân thức để rút gọn B

c) Biến đổi về phương trình bậc nhất rồi sử dụng: \(ax + b = 0\) có nghiệm duy nhất khi \(a \ne 0.\)

Lời giải chi tiết:

Cho hai biểu thức: \(A = \dfrac{{x - 2}}{x}\)  và \(B = \dfrac{{4x}}{{x + 1}} + \dfrac{x}{{1 - x}} + \dfrac{{2x}}{{{x^2} - 1}}\)  với \(x \ne  \pm 1;x \ne 0\)

a) Tính giá trị của biểu thức A khi \(x = \dfrac{2}{3}\)

Thay \(x = \dfrac{2}{3}\) (thỏa mãn điều kiện) vào biểu thức \(A\) ta được:

\(A = \dfrac{{\dfrac{2}{3} - 2}}{{\dfrac{2}{3}}}\) \( = \dfrac{{\dfrac{{ - 4}}{3}}}{{\dfrac{2}{3}}} =  - 2\)

Vậy với \(x = \dfrac{2}{3}\) thì \(A =  - 2.\)

b) Chứng minh rằng: \(B = \dfrac{{3x}}{{x + 1}}\)

Với \(x \ne  \pm 1;x \ne 0\) ta có:

\(B = \dfrac{{4x}}{{x + 1}} + \dfrac{x}{{1 - x}} + \dfrac{{2x}}{{{x^2} - 1}}\)

\( = \dfrac{{4x}}{{x + 1}} - \dfrac{x}{{x - 1}} + \dfrac{{2x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)

\( = \dfrac{{4x\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \dfrac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\) \( + \dfrac{{2x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)

\(\begin{array}{l} = \dfrac{{4x\left( {x - 1} \right) - x\left( {x + 1} \right) + 2x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \dfrac{{4{x^2} - 4x - {x^2} - x + 2x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \dfrac{{3{x^2} - 3x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \dfrac{{3x\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \dfrac{{3x}}{{x + 1}}\end{array}\)

Vậy \(B = \dfrac{{3x}}{{x + 1}}\)  với \(x \ne  \pm 1;x \ne 0\)

c) Cho \(P = A.B.\) Tìm tất cả các giá trị của \(m\) để phương trình \(P = m\) có nghiệm duy nhất.

Với \(x \ne  \pm 1;x \ne 0\) ta có:

\(P = A.B\) \( = \dfrac{{x - 2}}{x}.\dfrac{{3x}}{{x + 1}}\) \( = \dfrac{{3\left( {x - 2} \right)}}{{x + 1}}\)

Xét phương trình \(P = m\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{3\left( {x - 2} \right)}}{{x + 1}} = m\\ \Rightarrow 3\left( {x - 2} \right) = m\left( {x + 1} \right)\\ \Leftrightarrow 3x - 6 = mx + m\\ \Leftrightarrow mx - 3x + m + 6 = 0\\ \Leftrightarrow \left( {m - 3} \right)x + m + 6 = 0\left( * \right)\end{array}\)

Để phương trình \(P = m\) có nghiệm duy nhất thì phương trình (*) có nghiệm duy nhất khác \( \pm 1\) và khác \(0\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m - 3 \ne 0\\\left( {m - 3} \right).1 + m + 6 \ne 0\\\left( {m - 3} \right).\left( { - 1} \right) + m + 6 \ne 0\\\left( {m - 3} \right).0 + m + 6 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 3\\2m + 3 \ne 0\\9 \ne 0\\m + 6 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 3\\m \ne  - \dfrac{3}{2}\\m \ne  - 6\end{array} \right.\end{array}\) 

Vậy với \(m \ne 3;m \ne  - \dfrac{3}{2};m \ne  - 6\) thì phương trình \(P = m\) có nghiệm duy nhất.

---

LG bài 2

Phương pháp giải:

Giải bài toán bằng cách lập phương trình 

Bước 1: Chọn ẩn và đặt điều kiện cho ẩn

Bước 2: Lập phương trình và giải phương trình

Bước 3: Kết hợp điều kiện và kết luận

Lời giải chi tiết:

Một người đi xe máy từ A đến B với vận tốc \(50\) km/h, sau đó 30 phút, một ôtô cũng xuất phát từ A đến B với vận tốc 60 km/h. Tính độ dài quãng đường AB biết cả 2 xe đến B cùng lúc.

Gọi quãng đường AB là \(x\) (km) \(\left( {x > 0} \right)\)

Thời gian xe máy đi từ A đến B là \(\dfrac{x}{{50}}\) giờ

Thời gian ô tô đi từ A đến B là \(\dfrac{x}{{60}}\) giờ

Vì ô tô xuất phát muộn hơn xe máy 30 phút \( = \dfrac{1}{2}\) giờ nên thời gian xe máy đi từ A đến B sẽ nhiều hơn thời gian ô tô đi từ A đến B là \(\dfrac{1}{2}\) giờ. Ta có phương trình:

\(\begin{array}{l}\dfrac{x}{{50}} - \dfrac{x}{{60}} = \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{6x - 5x}}{{300}} = \dfrac{{150}}{{300}}\end{array}\)

\( \Leftrightarrow x = 150\) (thỏa mãn) 

Vậy quãng đường AB dài 150km.

---

LG bài 3

Phương pháp giải:

a) Đưa về giải phương trình \(A\left( x \right).B\left( x \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)

b) Giải phương trình chứa ẩn ở mẫu

B1: Đặt điều kiện và quy đồng mẫu thức

B2: Bỏ mẫu, chuyển vế đưa về giải phương trình \(A\left( x \right).B\left( x \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)

B3: So sánh điều kiện và kết luận nghiệm 

c) Nhân phá ngoặc rồi đưa về giải bất phương trình bậc nhất 1 ẩn.

d) Chuyển vế, đặt nhân tử chung và đánh giá.

Lời giải chi tiết:

a) \(3x\left( {x - 2} \right) = {x^2} - 4\)

\(\begin{array}{l} \Leftrightarrow 3x\left( {x - 2} \right) = \left( {x - 2} \right)\left( {x + 2} \right)\\ \Leftrightarrow 3x\left( {x - 2} \right) - \left( {x - 2} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {3x - x - 2} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {2x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\2x - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\2x = 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\end{array}\)

Vậy phương trình có tập nghiệm \(S = \left\{ {1;2} \right\}\)

b) \(\dfrac{{x + 3}}{{x - 1}} + \dfrac{x}{{x + 1}} = \dfrac{{{x^2} + 4x + 5}}{{{x^2} - 1}}\)  Điều kiện: \(x \ne  \pm 1\)

\( \Leftrightarrow \dfrac{{\left( {x + 3} \right)\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \dfrac{{x\left( {x - 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\) \( = \dfrac{{{x^2} + 4x + 5}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)

\( \Rightarrow \left( {x + 3} \right)\left( {x + 1} \right) + x\left( {x - 1} \right)\) \( = {x^2} + 4x + 5\)

\( \Leftrightarrow {x^2} + 3x + x + 3 + {x^2} - x\) \( = {x^2} + 4x + 5\)

\(\begin{array}{l} \Leftrightarrow 2{x^2} + 4x + 3 - x = {x^2} + 4x + 5\\ \Leftrightarrow 2{x^2} + 4x + 3 - x - {x^2} - 4x - 5 = 0\\ \Leftrightarrow {x^2} - x - 2 = 0\end{array}\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 2x + x - 2 = 0\\ \Leftrightarrow x\left( {x - 2} \right) + \left( {x - 2} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x + 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\left( {tm} \right)\\x =  - 1\left( {ktm} \right)\end{array} \right.\end{array}\)

Vậy phương trình có nghiệm \(x = 2.\)

c) \(3\left( {x - 1} \right) < 5\left( {x + 1} \right) - 2\)

\(\begin{array}{l} \Leftrightarrow 3x - 3 < 5x + 5 - 2\\ \Leftrightarrow 3x - 5x < 5 - 2 + 3\\ \Leftrightarrow  - 2x < 6\\ \Leftrightarrow x >  - 3\end{array}\)

Tập nghiệm của bất phương trình là \(S = \left\{ {x|x >  - 3} \right\}\)

d) \({x^3} >  - 2x\) 

\(\begin{array}{l} \Leftrightarrow {x^3} + 2x > 0\\ \Leftrightarrow x\left( {{x^2} + 2} \right) > 0\end{array}\)

\( \Leftrightarrow x > 0\) (vì \({x^2} \ge 0\) với mọi \(x\) nên \({x^2} + 2 \ge 2 > 0\) với mọi \(x\))

Tập nghiệm của bất phương trình là \(S = \left\{ {x|x > 0} \right\}\)

---

LG bài 4

Phương pháp giải:

a) Chứng minh hai tam giác BHA và BAC đồng dạng theo trường hợp góc – góc.

Từ đó suy ra cặp cạnh tương ứng tỉ lệ và suy ra đẳng thức cần chứng minh.

b) Chứng minh \(\Delta CHI \backsim \Delta CKB\) theo trường hợp góc – góc.

Từ đó suy ra tỉ số các cặp cạnh tương ứng và đẳng thức cần CM.

c) Chứng minh tỉ số \(\dfrac{{BH}}{{BD}} = \dfrac{{BK}}{{BC}}\) suy ra hai tam giác \(BHK\) và \(BDC\) đồng dạng theo trường hợp cạnh – góc – cạnh.

Từ đó suy ra cặp góc tương ứng bằng nhau.

d) Chứng minh đẳng thức \(B{M^2} = BK.BD\) từ việc sử dụng kết quả câu a, c và giả thiết BA=BM.

Từ đó suy ra hai tam giác BKM và BMD đồng dạng và suy ra cặp góc tương ứng bằng nhau.

Lời giải chi tiết:

Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), đường cao AH 

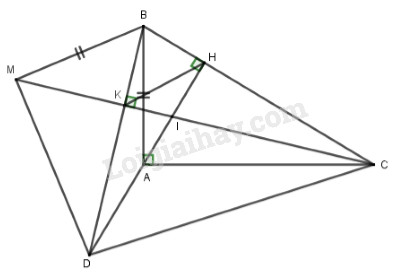
a) Chứng minh rằng \(\Delta BHA \backsim \Delta BAC\). Từ đó suy ra \(B{A^2} = BH.BC\)

Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\).

Ta có: \(AH \bot BC \Rightarrow \widehat {AHB} = {90^0}\).

Xét \(\Delta BHA\) và \(\Delta BAC\) có:

\(\begin{array}{l}\widehat {AHB} = \widehat {BAC} = {90^0}\\\widehat B\,\,\,chung\\ \Rightarrow \Delta BHA \backsim \Delta BAC\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{BA}}{{BC}}\)(cạnh tương ứng)

\( \Rightarrow BH.BC = B{A^2}\) (đpcm).

b) Lấy điểm I thuộc AH. Kẻ đường thẳng đi qua B và vuông góc với CI tại K. Chứng minh rằng \(CH.CB = CI.CK\)

Ta có: \(BK \bot CK \Rightarrow \widehat {BKC} = {90^0}\)

\(AH \bot BC \Rightarrow \widehat {CHI} = {90^0}\).

Xét \(\Delta CHI\) và \(\Delta CKB\) có:

\(\begin{array}{l}\widehat C\,\,\,chung\\\widehat {CHI} = \widehat {CKB} = {90^0}\\ \Rightarrow \Delta CHI \backsim \Delta CKB\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{CH}}{{CK}} = \dfrac{{CI}}{{CB}}\) (cạnh tương ứng)

\( \Rightarrow CH.CB = CK.CI\) (đpcm)

c) Tia BK cắt tia HA tại D. Chứng minh rằng \(\widehat {BHK} = \widehat {BDC}\)

Xét \(\Delta BHD\) và \(\Delta BKC\) có:

\(\begin{array}{l}\widehat {BKC} = \widehat {BHD} = {90^0}\\\widehat B\,\,\,chung\\ \Rightarrow \Delta BHD \backsim \Delta BKC\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{BH}}{{BK}} = \dfrac{{BD}}{{BC}}\) (cạnh tương ứng)

\( \Rightarrow \dfrac{{BH}}{{BD}} = \dfrac{{BK}}{{BC}}\).

Xét \(\Delta BHK\) và \(\Delta BDC\) có:

\(\begin{array}{l}\dfrac{{BH}}{{BD}} = \dfrac{{BK}}{{BC}}\,\left( {cmt} \right)\\\widehat B\,\,\,chung\\ \Rightarrow \Delta BHK \backsim \Delta BDC\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow \widehat {BHK} = \widehat {BDC}\) (góc tương ứng) (đpcm).

d) Trên tia đối của tia KC lấy điểm M sao cho \(BM = BA.\) Chứng minh rằng \(\widehat {BMD} = {90^0}\) .

Từ câu a ta có: \(B{A^2} = BH.BC\).

Mà \(BM = BA\) nên \(B{M^2} = BH.BC\)  (1)

Từ câu c ta có: \(\dfrac{{BH}}{{BD}} = \dfrac{{BK}}{{BC}}\) \( \Rightarrow BH.BC = BK.BD\)  (2)

Từ (1) và (2) suy ra \(B{M^2} = BK.BD\) \(\left( { = BH.BC} \right)\)

\( \Rightarrow \dfrac{{BM}}{{BK}} = \dfrac{{BD}}{{BM}}\)

Xét \(\Delta BMD\) và \(\Delta BKM\) có:

\(\begin{array}{l}\widehat B\,\,\,chung\\\dfrac{{BM}}{{BK}} = \dfrac{{BD}}{{BM}}\,\left( {cmt} \right)\\ \Rightarrow \Delta BMD \backsim \Delta BKM\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow \widehat {BMD} = \widehat {BKM}\) (góc tương ứng)

Mà \(\widehat {BKM} = {90^0}\) nên \(\widehat {BMD} = {90^0}\) (đpcm).

---

LG bài 5

Phương pháp giải:

Biến đổi M về làm xuất hiện hằng đẳng thức. 

Sử dụng đánh giá \({A^2} \ge 0\) và BĐT Cô – si cho hai số dương \(a,b\) là \(a + b \ge 2\sqrt {ab} \).

Lời giải chi tiết:

Cho \(x > 0.\) Tìm giá trị nhỏ nhất của biểu thức: \(M = 4{x^2} - 3x + \dfrac{1}{{4x}} + 2020\)

Ta có:

\(\begin{array}{l}M = 4{x^2} - 3x + \dfrac{1}{{4x}} + 2020\\ = 4{x^2} - 4x + x + \dfrac{1}{{4x}} + 1 + 2019\\ = \left( {4{x^2} - 4x + 1} \right) + \left( {x + \dfrac{1}{{4x}}} \right) + 2019\\ = {\left( {2x - 1} \right)^2} + \left( {x + \dfrac{1}{{4x}}} \right) + 2019\end{array}\)

Ta có: \({\left( {2x - 1} \right)^2} \ge 0\) với mọi \(x > 0\).

Áp dụng BĐT Cô – si cho hai số dương là \(x\) và \(\dfrac{1}{{4x}}\) ta có:

\(x + \dfrac{1}{{4x}} \ge 2\sqrt {x.\dfrac{1}{{4x}}} \) \( = 2.\sqrt {\dfrac{1}{4}}  = 2.\dfrac{1}{2} = 1\)

\( \Rightarrow M \ge 0 + 1 + 2019 = 2020\)

Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}2x - 1 = 0\\x = \dfrac{1}{{4x}}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2x = 1\\4{x^2} = 1\end{array} \right. \Leftrightarrow x = \dfrac{1}{2}\)

Vậy GTNN của M là \(2020\) khi \(x = \dfrac{1}{2}\).

HẾT