Đề thi học kì 2 môn toán lớp 8 năm 2019 - 2020 trường THCS Dịch Vọng

Đề bài

Bài 1  (2,0 điểm): Cho biểu thức: \(A = \left( {\dfrac{2}{{x - 1}} + \dfrac{3}{{x + 1}} - \dfrac{{2x + 2}}{{{x^2} - 1}}} \right).\dfrac{{{x^2} + x}}{{3x + 9}}\)  với \(x \ne  - 3;x \ne  \pm 1\)

a) Chứng minh \(A = \dfrac{x}{{x + 3}}\)

b) Tính giá trị của biểu thức \(A\) khi \(\left| {x - 2} \right| = 1\)

c) Tìm \(x\) để \(A < 1.\)

Bài 2 (2,0 điểm): Giải bài toán sau bằng cách lập phương trình.

Trong thời gian nghỉ do dịch Covid-19, An dự định tự ôn tập kiến thức bằng cách làm thêm các bài tập trong sách tham khảo. Lúc đầu An dự định sẽ hoàn thành trong 40 ngày. Nhưng thực tế, mỗi ngày An làm được nhiều hơn 1 bài nên đã hoàn thành số bài tập đó sớm hơn dự định 2 ngày. Hỏi thực tế mỗi ngày An làm được bao nhiêu bài tập?

Bài 3 (2,0 điểm): Giải các phương trình sau:

a) \(\left( {x + 1} \right)\left( {x - 2} \right) = 2\left( {{x^2} - 4} \right)\)

b) \(\left| {x - 2} \right| + 3 = 2x\)

c) \(\dfrac{3}{{x - 7}} + \dfrac{2}{{x + 7}} = \dfrac{5}{{{x^2} - 49}}\)

d) \(\dfrac{{2x - 1}}{3} - \dfrac{{x + 3}}{2} > 1 + \dfrac{{5x}}{6}\)

Bài 4 (3,5 điểm):

1. Cho \(\Delta ABC\) vuông tại A có AH là đường cao.

a) Chứng minh: \(\Delta HAC \backsim \Delta ABC\)

b) Vẽ \(HD \bot AB\left( {D \in AB} \right),\) \(HE \bot AC\left( {E \in AC} \right).\) Chứng minh \(A{H^2} = AD.AB\)

c) Chứng minh: \(AD.AB = AE.AC\)

d) Tính tỉ số \(\dfrac{{{S_{\Delta ADE}}}}{{{S_{\Delta ACB}}}}\). Biết \(AB = 12cm,AC = 16cm.\)

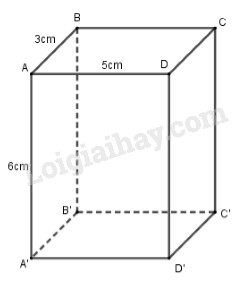
2. Cho hình hộp chữ nhật có \(AB = 3cm,AD = 5cm,\) \(AA' = 6cm\) như hình bên. Tính diện tích xung quanh và thể tích của hình hộp chữ nhật.

Bài 5 (0,5 điểm):

Tìm giá trị nhỏ nhất và giá trị lớn nhất của \(A = \dfrac{{27 - 12x}}{{{x^2} + 9}}\). 

HẾT

---

LG bài 1

Phương pháp giải:

a) Qui đồng mẫu các phân thức, cộng trừ và rút gọn các phân thức 

b) Tìm x sau đó thay giá trị của x thỏa mãn điều kiện vào biểu thức A để tính toán

c) Đưa về giải bất phương trình, chú ý rằng \(\dfrac{B}{C} < 0\) thì B và C trái dấu 

Lời giải chi tiết:

Cho biểu thức: \(A = \left( {\dfrac{2}{{x - 1}} + \dfrac{3}{{x + 1}} - \dfrac{{2x + 2}}{{{x^2} - 1}}} \right).\dfrac{{{x^2} + x}}{{3x + 9}}\)  với \(x \ne  - 3;x \ne  \pm 1\)

a) Chứng minh \(A = \dfrac{x}{{x + 3}}\)

Với \(x \ne  - 3;x \ne  \pm 1\) ta có: \(A = \left( {\dfrac{2}{{x - 1}} + \dfrac{3}{{x + 1}} - \dfrac{{2x + 2}}{{{x^2} - 1}}} \right).\dfrac{{{x^2} + x}}{{3x + 9}}\)

\( = \left[ {\dfrac{{2\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \dfrac{{3\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \dfrac{{2x + 2}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}} \right]\)\(.\dfrac{{{x^2} + x}}{{3x + 9}}\)

\( = \dfrac{{2\left( {x + 1} \right) + 3\left( {x - 1} \right) - \left( {2x + 2} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\) \(.\dfrac{{x\left( {x + 1} \right)}}{{3\left( {x + 3} \right)}}\)

\(\begin{array}{l} = \dfrac{{2x + 2 + 3x - 3 - 2x - 2}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.\dfrac{{x\left( {x + 1} \right)}}{{3\left( {x + 3} \right)}}\\ = \dfrac{{3x - 3}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.\dfrac{{x\left( {x + 1} \right)}}{{3\left( {x + 3} \right)}}\\ = \dfrac{{3\left( {x - 1} \right).x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right).3\left( {x + 3} \right)}}\\ = \dfrac{x}{{x + 3}}\end{array}\)

Vậy \(A = \dfrac{x}{{x + 3}}\) với \(x \ne  - 3;x \ne  \pm 1\).

b) Tính giá trị của biểu thức \(A\) khi  \(\left| {x - 2} \right| = 1\)

Ta có: \(\left| {x - 2} \right| = 1\) \( \Leftrightarrow \left[ \begin{array}{l}x - 2 = 1\\x - 2 =  - 1\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)

Mà điều kiện \(x \ne  - 3;x \ne  \pm 1\) nên chỉ có \(x = 3\) thỏa mãn.

Thay \(x = 3\) vào biểu thức \(A = \dfrac{x}{{x + 3}}\) ta được:

\(A = \dfrac{3}{{3 + 3}}\) \( = \dfrac{3}{6} = \dfrac{1}{2}\)

Vậy \(A = \dfrac{1}{2}\) khi \(\left| {x - 2} \right| = 1\)

c) Tìm \(x\) để \(A < 1.\)

Để \(A < 1\) thì \(\dfrac{x}{{x + 3}} < 1\) với \(x \ne  - 3;x \ne  \pm 1\)

\(\begin{array}{l} \Leftrightarrow \dfrac{x}{{x + 3}} - 1 < 0\\ \Leftrightarrow \dfrac{x}{{x + 3}} - \dfrac{{x + 3}}{{x + 3}} < 0\\ \Leftrightarrow \dfrac{{x - x - 3}}{{x + 3}} < 0\\ \Leftrightarrow \dfrac{{ - 3}}{{x + 3}} < 0\end{array}\) 

Vì \( - 3 < 0\) nên \(\dfrac{{ - 3}}{{x + 3}} < 0 \Leftrightarrow x + 3 > 0\) \( \Leftrightarrow x >  - 3\)

Kết hợp điều kiện \(x \ne  - 3;x \ne  \pm 1\) ta có \(x >  - 3;x \ne  \pm 1\)

Vậy với \(x >  - 3;x \ne  \pm 1\) thì \(A < 1.\)

---

LG bài 2

Phương pháp giải:

Giải bài toán bằng cách lập phương trình 

Bước 1: Chọn ẩn và đặt điều kiện cho ẩn

Bước 2: Lập phương trình và giải phương trình

Bước 3: Kết hợp điều kiện và kết luận

Lời giải chi tiết:

Gọi số bài tập thực tế mỗi ngày An làm được là: \(x\) (bài) \(\left( {x > 1} \right)\)

Số bài tập An làm mỗi ngày theo dự định là: \(x - 1\) (bài)

Tổng số bài tập An làm là: \(40\left( {x - 1} \right)\) bài

Thời gian An làm bài theo thực tế là \(\dfrac{{40\left( {x - 1} \right)}}{x}\)  ngày

Vì An đã hoàn thành số bài tập đó sớm hơn dự định 2 ngày nên thực tế An làm trong \(40 - 2 = 38\) ngày

Ta có phương trình:

\(\begin{array}{l}\dfrac{{40\left( {x - 1} \right)}}{x} = 38\\ \Rightarrow 40\left( {x - 1} \right) = 38x\\ \Leftrightarrow 40x - 40 = 38x\\ \Leftrightarrow 40x - 38x = 40\\ \Leftrightarrow 2x = 40\end{array}\)

\( \Leftrightarrow x = 20\) (thỏa mãn) 

Vậy theo thực tế mỗi ngày An làm được \(20\) bài tập.

---

LG bài 3

Phương pháp giải:

a) Nhân đa thức với đa thức, chuyển vế rút gọn đưa về giải phương trình bậc nhất 1 ẩn

b) Phá dấu giá trị tuyệt đối \(\left| A \right| = A\) khi \(A \ge 0\) và \(\left| A \right| =  - A\) khi \(A < 0\)

c) Giải phương trình chứa ẩn ở mẫu 

B1: Đặt điều kiện và quy đồng mẫu thức

B2: Bỏ mẫu, chuyển vế đưa về giải phương trình bậc nhất 1 ẩn

B3: So sánh điều kiện và kết luận nghiệm

d) Quy đồng mẫu rồi đưa về giải bất phương trình bậc nhất 1 ẩn.

Lời giải chi tiết:

a) \(\left( {x + 1} \right)\left( {x - 2} \right) = 2\left( {{x^2} - 4} \right)\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 2x + x - 2 = 2{x^2} - 8\\ \Leftrightarrow {x^2} - x - 2 = 2{x^2} - 8\\ \Leftrightarrow {x^2} - x - 2 - 2{x^2} + 8 = 0\\ \Leftrightarrow  - {x^2} - x + 6 = 0\\ \Leftrightarrow {x^2} + x - 6 = 0\\ \Leftrightarrow {x^2} - 2x + 3x - 6 = 0\\ \Leftrightarrow x\left( {x - 2} \right) + 3\left( {x - 2} \right) = 0\\ \Leftrightarrow \left( {x + 3} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 3\\x = 2\end{array} \right.\end{array}\)

Vậy phương trình có tập nghiệm \(S = \left\{ { - 3;2} \right\}\)

b) \(\left| {x - 2} \right| + 3 = 2x\)

\( \Leftrightarrow \left| {x - 2} \right| = 2x - 3\)

TH1: \(x - 2 \ge 0 \Leftrightarrow x \ge 2\) \( \Rightarrow \left| {x - 2} \right| = x - 2\)

Khi đó ta có phương trình:

\(\begin{array}{l}x - 2 = 2x - 3\\ \Leftrightarrow x - 2x = 2 - 3\\ \Leftrightarrow  - x =  - 1\end{array}\)

\( \Leftrightarrow x = 1\) (không thỏa mãn)

TH2: \(x - 2 < 0 \Leftrightarrow x < 2\)

\( \Rightarrow \) \(\left| {x - 2} \right| =  - \left( {x - 2} \right)\)\( = 2 - x\)

Khi đó ta có phương trình:

\(\begin{array}{l}2 - x = 2x - 3\\ \Leftrightarrow  - x - 2x =  - 2 - 3\\ \Leftrightarrow  - 3x =  - 5\end{array}\)

\( \Leftrightarrow x = \dfrac{5}{3}\)  (thỏa mãn)

Vậy phương trình có nghiệm \(x = \dfrac{5}{3}.\)

c) \(\dfrac{3}{{x - 7}} + \dfrac{2}{{x + 7}} = \dfrac{5}{{{x^2} - 49}}\)  Điều kiện: \(x \ne  \pm 7\)

\( \Leftrightarrow \dfrac{{3\left( {x + 7} \right)}}{{\left( {x - 7} \right)\left( {x + 7} \right)}} + \dfrac{{2\left( {x - 7} \right)}}{{\left( {x + 7} \right)\left( {x - 7} \right)}}\) \( = \dfrac{5}{{\left( {x - 7} \right)\left( {x + 7} \right)}}\)

\( \Leftrightarrow \dfrac{{3\left( {x + 7} \right) + 2\left( {x - 7} \right)}}{{\left( {x - 7} \right)\left( {x + 7} \right)}} = \dfrac{5}{{\left( {x - 7} \right)\left( {x + 7} \right)}}\)

\(\begin{array}{l} \Rightarrow 3\left( {x + 7} \right) + 2\left( {x - 7} \right) = 5\\ \Leftrightarrow 3x + 21 + 2x - 14 = 5\\ \Leftrightarrow 5x + 7 = 5\\ \Leftrightarrow 5x =  - 2\end{array}\)

\( \Leftrightarrow x =  - \dfrac{2}{5}\) (thỏa mãn)

Vậy phương trình có nghiệm \(x =  - \dfrac{2}{5}\).

d) \(\dfrac{{2x - 1}}{3} - \dfrac{{x + 3}}{2} > 1 + \dfrac{{5x}}{6}\) 

\(\begin{array}{l} \Leftrightarrow \dfrac{{\left( {2x - 1} \right).2}}{6} - \dfrac{{3\left( {x + 3} \right)}}{6} > \dfrac{6}{6} + \dfrac{{5x}}{6}\\ \Leftrightarrow \dfrac{{4x - 2 - 3x - 9}}{6} > \dfrac{{6 + 5x}}{6}\\ \Leftrightarrow \dfrac{{x - 11}}{6} > \dfrac{{5x + 6}}{6}\\ \Leftrightarrow x - 11 > 5x + 6\\ \Leftrightarrow x - 5x > 6 + 11\\ \Leftrightarrow  - 4x > 17\\ \Leftrightarrow x <  - \dfrac{{17}}{4}\end{array}\)

Vậy tập nghiệm của bất phương trình \(S = \left\{ {x|x <  - \dfrac{{17}}{4}} \right\}\)

---

LG bài 4

Phương pháp giải:

1)

a) Chứng minh hai tam giác đồng dạng theo trường hợp góc – góc.

b) Chứng minh \(\Delta AHD \backsim \Delta ABH\left( {g - g} \right)\)

Từ đó suy ra tỉ lệ các cạnh tương ứng.

c) Chứng minh \(A{H^2} = AE.AC\) suy ra đpcm.

d) Chứng minh \(\Delta ADE \backsim \Delta ACB\).

Tính độ dài \(BC,DE\) suy ra tỉ lệ diện tích.

Sử dụng kết quả: Nếu hai tam giác đồng dạng thì tỉ lệ diện tích bằng bình phương tỉ số đồng dạng.

2) 

Diện tích xung quanh hình hộp bằng chu vi đáy nhân chiều cao.

Thể tích hình hộp chữ nhật: \(V = abc\) với \(a,b,c\) là các kích thước của hình hộp chữ nhật

Lời giải chi tiết:

1. Cho \(\Delta ABC\) vuông tại A có AH là đường cao. 

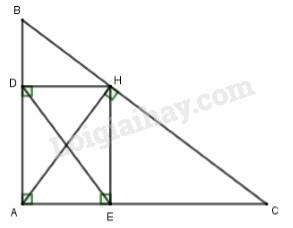
a) Chứng minh: \(\Delta HAC \backsim \Delta ABC\)

Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\).

Ta có: \(AH \bot BC \Rightarrow \widehat {AHC} = {90^0}\).

Xét \(\Delta HAC\) và \(\Delta ABC\) có:

\(\begin{array}{l}\widehat {AHC} = \widehat {BAC} = {90^0}\\\widehat C\,\,\,\,\,\,chung\\ \Rightarrow \Delta HAC \backsim \Delta ABC\left( {g - g} \right)\end{array}\)

\( \Rightarrow \) đpcm.

b) Vẽ \(HD \bot AB\left( {D \in AB} \right),\) \(HE \bot AC\left( {E \in AC} \right).\) Chứng minh \(A{H^2} = AD.AB\)

Ta có: \(HD \bot AB \Rightarrow \widehat {ADH} = {90^0}\)

Xét tam giác \(AHD\) và tam giác \(ABH\) có:

\(\begin{array}{l}\widehat {ADH} = \widehat {AHB} = {90^0}\\\widehat B\,\,\,chung\\ \Rightarrow \Delta AHD \backsim \Delta ABH\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{AH}}{{AB}} = \dfrac{{AD}}{{AH}}\) (cạnh tương ứng)

\( \Rightarrow A{H^2} = AD.AB\left( {dpcm} \right)\).

c) Chứng minh: \(AD.AB = AE.AC\)

Ta có: \(HE \bot AC \Rightarrow \widehat {AEH} = {90^0}\)

Xét tam giác \(AHE\) và tam giác \(ACH\) có:

\(\begin{array}{l}\widehat {AEH} = \widehat {AHC} = {90^0}\\\widehat C\,\,\,chung\\ \Rightarrow \Delta AHE \backsim \Delta ACH\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AE}}{{AH}}\) (cạnh tương ứng)

\( \Rightarrow A{H^2} = AE.AC\).

Mà \(A{H^2} = AD.AB\) (theo câu b)

\( \Rightarrow AD.AB = AE.AC\left( { = A{H^2}} \right)\) (đpcm)

d)  Tính tỉ số \(\dfrac{{{S_{\Delta ADE}}}}{{{S_{\Delta ACB}}}}\). Biết \(AB = 12cm,AC = 16cm.\)

Theo câu c, \(AD.AB = AE.AC\) \( \Rightarrow \dfrac{{AD}}{{AC}} = \dfrac{{AE}}{{AB}}\)

Xét \(\Delta ADE\) và \(\Delta ACB\) có:

\(\begin{array}{l}\widehat A\,\,\,chung\\\dfrac{{AD}}{{AC}} = \dfrac{{AE}}{{AB}}\left( {cmt} \right)\\ \Rightarrow \Delta ADE \backsim \Delta ACB\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow \dfrac{{AD}}{{AC}} = \dfrac{{AE}}{{AB}} = \dfrac{{DE}}{{BC}} = k\) với \(k\) là tỉ số đồng dạng của hai tam giác \(ADE\) và \(ACB\).

Xét tam giác ABC vuông tại A có \(AB = 12,AC = 16\).

Áp dụng định lý Pitago ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ = {12^2} + {16^2} = 400 = {20^2}\\ \Rightarrow BC = 20\end{array}\)

Ta có:

\(\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}AH.BC\\ \Rightarrow AB.AC = AH.BC\\ \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{12.16}}{{20}} = 9,6\end{array}\)

Xét tứ giác AEHD có \(\widehat A = \widehat D = \widehat E = {90^0}\) nên là hình chữ nhật.

\( \Rightarrow DE = AH = 9,6\) (tính chất)

\( \Rightarrow k = \dfrac{{DE}}{{BC}} = \dfrac{{9,6}}{{20}} = \dfrac{{12}}{{25}}\)

Vậy \(\dfrac{{{S_{\Delta ADE}}}}{{{S_{\Delta ACB}}}} = {k^2} = {\left( {\dfrac{{12}}{{25}}} \right)^2} = \dfrac{{144}}{{625}}\).

2) Cho hình hộp chữ nhật có \(AB = 3cm,AD = 5cm,\) \(AA' = 6cm\) như hình bên. Tính diện tích xung quanh và thể tích của hình hộp chữ nhật.

Chu vi hình chữ nhật ABCD là: \(\left( {3 + 5} \right).2 = 16\left( {cm} \right)\)

Diện tích xung quanh hình hộp chữ nhật là: \(16.6 = 96\left( {c{m^2}} \right)\).

Thể tích hình hộp chữ nhật là: \(3.5.6 = 90\left( {c{m^3}} \right)\).

---

LG bài 5

Phương pháp giải:

Biến đổi A về dạng \(A = {A_1} - \dfrac{{B_1^2}}{{{x^2} + 9}} = {A_2} + \dfrac{{B_2^2}}{{{x^2} + 9}}\)

Từ đó suy ra \({A_2} \le A \le {A_1}\).

Lời giải chi tiết:

Tìm giá trị nhỏ nhất và giá trị lớn nhất của \(A = \dfrac{{27 - 12x}}{{{x^2} + 9}}\) .

Ta có:

\(\begin{array}{l}A = \dfrac{{27 - 12x}}{{{x^2} + 9}}\\ = \dfrac{{{x^2} - 12x + 36 - 9 - {x^2}}}{{{x^2} + 9}}\\ = \dfrac{{{{\left( {x - 6} \right)}^2} - \left( {{x^2} + 9} \right)}}{{{x^2} + 9}}\\ = \dfrac{{{{\left( {x - 6} \right)}^2}}}{{{x^2} + 9}} - \dfrac{{{x^2} + 9}}{{{x^2} + 9}}\\ = \dfrac{{{{\left( {x - 6} \right)}^2}}}{{{x^2} + 9}} - 1\end{array}\)

Vì \({\left( {x - 6} \right)^2} \ge 0\) và \({x^2} \ge 0 \Rightarrow {x^2} + 9 > 0\) với mọi \(x\) nên \(\dfrac{{{{\left( {x - 6} \right)}^2}}}{{{x^2} + 9}} \ge 0\)

\( \Rightarrow \dfrac{{{{\left( {x - 6} \right)}^2}}}{{{x^2} + 9}} - 1 \ge 0 - 1 =  - 1\)

\( \Rightarrow A \ge  - 1\)

Dấu “=” xảy ra khi \(x - 6 = 0 \Leftrightarrow x = 6\).

Lại có,

\(\begin{array}{l}A = \dfrac{{27 - 12x}}{{{x^2} + 9}}\\ = \dfrac{{ - 4{x^2} - 12x - 9 + 36 + 4{x^2}}}{{{x^2} + 9}}\\ = \dfrac{{ - \left( {4{x^2} + 12x + 9} \right) + 4\left( {{x^2} + 9} \right)}}{{{x^2} + 9}}\\ = \dfrac{{ - {{\left( {2x + 3} \right)}^2} + 4\left( {{x^2} + 9} \right)}}{{{x^2} + 9}}\\ =  - \dfrac{{{{\left( {2x + 3} \right)}^2}}}{{{x^2} + 9}} + \dfrac{{4\left( {{x^2} + 9} \right)}}{{{x^2} + 9}}\\ =  - \dfrac{{{{\left( {2x + 3} \right)}^2}}}{{{x^2} + 9}} + 4\end{array}\)

Vì \({\left( {2x + 3} \right)^2} \ge 0\) và \({x^2} \ge 0 \Rightarrow {x^2} + 9 > 0\) với mọi \(x\) nên \(\dfrac{{{{\left( {2x + 3} \right)}^2}}}{{{x^2} + 9}} \ge 0\)

\(\begin{array}{l} \Rightarrow  - \dfrac{{{{\left( {2x + 3} \right)}^2}}}{{{x^2} + 9}} \le 0\\ \Rightarrow  - \dfrac{{{{\left( {2x + 3} \right)}^2}}}{{{x^2} + 9}} + 4 \le 0 + 4 = 4\\ \Rightarrow A \le 4\end{array}\)

Dấu “=” xảy ra khi \(2x + 3 = 0 \Leftrightarrow x =  - \dfrac{3}{2}\).

Vậy GTLN của A là \(4\) khi \(x =  - \dfrac{3}{2}\)

GTNN của A là \( - 1\) khi \(x = 6\).

HẾT