Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 7
Câu 1: Phát biểu nào sau đây là một mệnh đề? A. Mùa thu Hà Nội đẹp quá! B. Bạn có đi học không? C. Đề thi môn Toán khó quá! D. Hà Nội là thủ đô của Việt Nam.
Đề bài
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1: Phát biểu nào sau đây là một mệnh đề?
A. Mùa thu Hà Nội đẹp quá! B. Bạn có đi học không?
C. Đề thi môn Toán khó quá! D. Hà Nội là thủ đô của Việt Nam.
Câu 2: Cho số gần đúng \(a = 23748023\) với độ chính xác \(d = 101\). Hãy viết số quy tròn của số \(a.\)
A. \(23749000.\) B. \(23748000.\) C. \(23746000.\) D. \(23747000.\)
Câu 3: Cho tam giác \(ABC\) với \(M,\;N,\;P\) lần lượt là trung điểm của \(BC,\;CA,\;AB\). Khẳng định nào sau đây sai?
A. \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 .\) B. \(\overrightarrow {AP} + \overrightarrow {BM} + \overrightarrow {CN} = \overrightarrow 0 .\)
C. \(\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PM} = \overrightarrow 0 .\) D. \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {MP} .\)
Câu 4: Cho hình thoi \(ABCD\) cạnh bằng \(1\;cm\) và có \(\widehat {BAD} = 60^\circ \). Tính độ dài cạnh \(AC\).
A. \(AC = \sqrt 3 .\) B. \(AC = \sqrt 2 .\) C. \(AC = 2\sqrt 3 .\) D. \(AC = 2.\)
Câu 5: Cặp số (x;y) nào là sau đây không là nghiệm của bất phương trình \(2x - y + 3 > 0\).
A. (x;y) = (0;4). B. (x;y) = (2;5). C. (x;y) = (1;3). D. (x;y) = (1;4).
Câu 6: Cho tam giác \(ABC\) và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \). Mệnh đề nào sau đây sai?
A. \(MABC\) là hình bình hành. B. \(\overrightarrow {AM} + \overrightarrow {AB} = \overrightarrow {AC} .\)
C. \(\overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BM} .\) D. \(\overrightarrow {MA} = \overrightarrow {BC} .\)
Câu 7: Cho tam giác \(ABC\) có \(AB = 3\sqrt 3 ,{\rm{ }}BC = 6\sqrt 3 \) và \(CA = 9\). Gọi \(D\) là trung điểm \(BC\). Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABD.\)
A. \(R = \frac{9}{6}\). B. \(R = 3\). C. \(R = 3\sqrt 3 \). D. \(R = \frac{9}{2}\).
Câu 8: Cho hai vectơ \(\vec a\) và \(\overrightarrow b \). Đẳng thức nào sau đây sai?
A. \(\vec a.\overrightarrow b = \frac{1}{2}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} - {{\left| {\vec a} \right|}^2} - {{\left| {\overrightarrow b } \right|}^2}} \right).\) B. \(\vec a.\overrightarrow b = \frac{1}{2}\left( {{{\left| {\vec a} \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - {{\left| {\vec a - \overrightarrow b } \right|}^2}} \right).\)
C. \(\vec a.\overrightarrow b = \frac{1}{2}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} - {{\left| {\vec a - \overrightarrow b } \right|}^2}} \right).\) D. \(\vec a.\overrightarrow b = \frac{1}{4}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} - {{\left| {\vec a - \overrightarrow b } \right|}^2}} \right).\)
Câu 9: Cho \(A\) là tập hợp các hình thoi, \(B\) là tập hợp các hình chữ nhật và \(C\) là tập hợp các hình vuông. Khi đó
A. \(B\backslash A = C\). B. \(A \cup B = C\). C. \(A\backslash B = C\). D. \(A \cap B = C\).
Câu 10: Lớp 10A có \(45\) học sinh, trong đó có \(15\) học sinh được xếp loại học lực giỏi, \(20\) học sinh được xếp loại hạnh kiểm tốt, \(10\) em vừa được xếp loại học lực giỏi , vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt?
A. \(10\). B. \(35\). C. \(25\). D. \(45\).
Câu 11: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc \({60^0}\). Tàu thứ nhất chạy với tốc độ \(30\,km/h\), tàu thứ hai chạy với tốc độ \(40\,km/h\). Hỏi sau \(2\) giờ hai tàu cách nhau bao nhiêu \(km\)?
A. \(13.\) B. \(20\sqrt {13} .\) C. \(10\sqrt {13} .\) D. \(15.\)
Câu 12: Cho biết \(\tan \alpha = - 3.\) Giá trị của \(P = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }}\) bằng bao nhiêu?
A. \(P = \frac{4}{3}.\) B. \(P = \frac{5}{3}.\) C. \(P = - \frac{4}{3}.\) D. \(P = - \frac{5}{3}.\)
Câu 13: Cho \(A = \left( {2; + \infty } \right)\), \(B = \left( {m; + \infty } \right)\). Điều kiện cần và đủ của \(m\) sao cho \(B\) là tập con của \(A\) là
A. \(m \le 2\). B. \(m = 2\). C. \(m > 2\). D. \(m \ge 2\).
Câu 14: Tam giác \(ABC\) vuông ở \(A\) có góc \(\widehat B = {30^0}.\) Khẳng định nào sau đây là sai?
A. \(\cos B = \frac{1}{{\sqrt 3 }}.\) B. \(\sin C = \frac{{\sqrt 3 }}{2}.\) C. \(\cos C = \frac{1}{2}.\) D. \(\sin B = \frac{1}{2}.\)
Câu 15: Cho hình chữ nhật \(ABCD\) có \(AB = 8,{\rm{ }}AD = 5.\) Tích \(\overrightarrow {AB} .\overrightarrow {BD} .\)
A. \(\overrightarrow {AB} .\overrightarrow {BD} = 62.\) B. \(\overrightarrow {AB} .\overrightarrow {BD} = 64.\) C. \(\overrightarrow {AB} .\overrightarrow {BD} = - 62.\) D. \(\overrightarrow {AB} .\overrightarrow {BD} = - 64.\)
Câu 16: Cho tam giác \(ABC\) vuông cân tại \(C\) và \(AB = \sqrt 2 .\) Tính độ dài của \(\overrightarrow {AB} + \overrightarrow {AC} .\)
A. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \sqrt 5 .\) B. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2\sqrt 5 .\)
C. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \sqrt 3 .\) D. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2\sqrt 3 .\)
Câu 17: Tiền thưởng (triệu đồng) của cán bộ và nhân viên trong một công ty được cho ở bảng dưới đây:
|
Tiền thưởng |
1 |
2 |
3 |
4 |
5 |
Cộng |
|
Tần số |
10 |
12 |
11 |
15 |
2 |
50 |
Tìm Mốt \({M_0}\)?
A. \({M_0} = 4\) B. \({M_0} = 15\)
C. \({M_0} = 5\) D. \({M_0} = 11\)
Câu 18: Giả sử ta có một mẫu số liệu kích thước \(N\) là \(\left\{ {{x_1};{\mkern 1mu} {\mkern 1mu} {x_2};{\mkern 1mu} {\mkern 1mu} \ldots ;{\mkern 1mu} {\mkern 1mu} {x_N}} \right\}\). Khi đó, phương sai của mẫu số liệu này, kí hiệu là \({s^2}\) được tính bởi công thức nào sau đây?
A. \({s^2} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} - \bar x} \right)}^2}} \) B. \({s^2} = \frac{1}{N}{\left( {\sum\limits_{i = 1}^N {\left( {{x_i} - \bar x} \right)} } \right)^2}\) C. \({s^2} = N\sum\limits_{i = 1}^N {{{\left( {{x_i} - \bar x} \right)}^2}} \) D. \({s^2} = N{\left( {\sum\limits_{i = 1}^N {\left( {{x_i} - \bar x} \right)} } \right)^2}\)
Câu 19: Cho tam giác \(ABC\) có \(AB = 4\)cm, \(BC = 7\) cm, \(AC = 9\)cm. Tính \(\cos A\).
A. \(\cos A = - \frac{2}{3}\). B. \(\cos A = \frac{1}{2}\). C. \(\cos A = \frac{1}{3}\). D. \(\cos A = \frac{2}{3}\).
Câu 20: Một cửa hàng bán sách thống kê số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở cửa hàng trong một ngày. Số liệu được ghi trong bảng phân bố tần số sau:
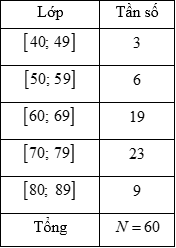
Số trung bình cộng và độ lệch chuẩn xấp xỉ bằng (kết quả được làm tròn đến chữ số thập phân thứ hai).
A. 69,34 và 10,26 B. 69,33 và 10,25 C. 10,25 và 69,33 D. 10,26 và 69,34
Câu 21: Miền nghiệm của bất phương trình: \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) - y + 3\) là nửa mặt phẳng chứa điểm:
A. \(\left( {3;0} \right).\) B. \(\left( {3;1} \right).\) C. \(\left( {2;1} \right).\) D. \(\left( {0;0} \right).\)
Câu 22: Phần không bị gạch trong hình vẽ dưới đây (không kể biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
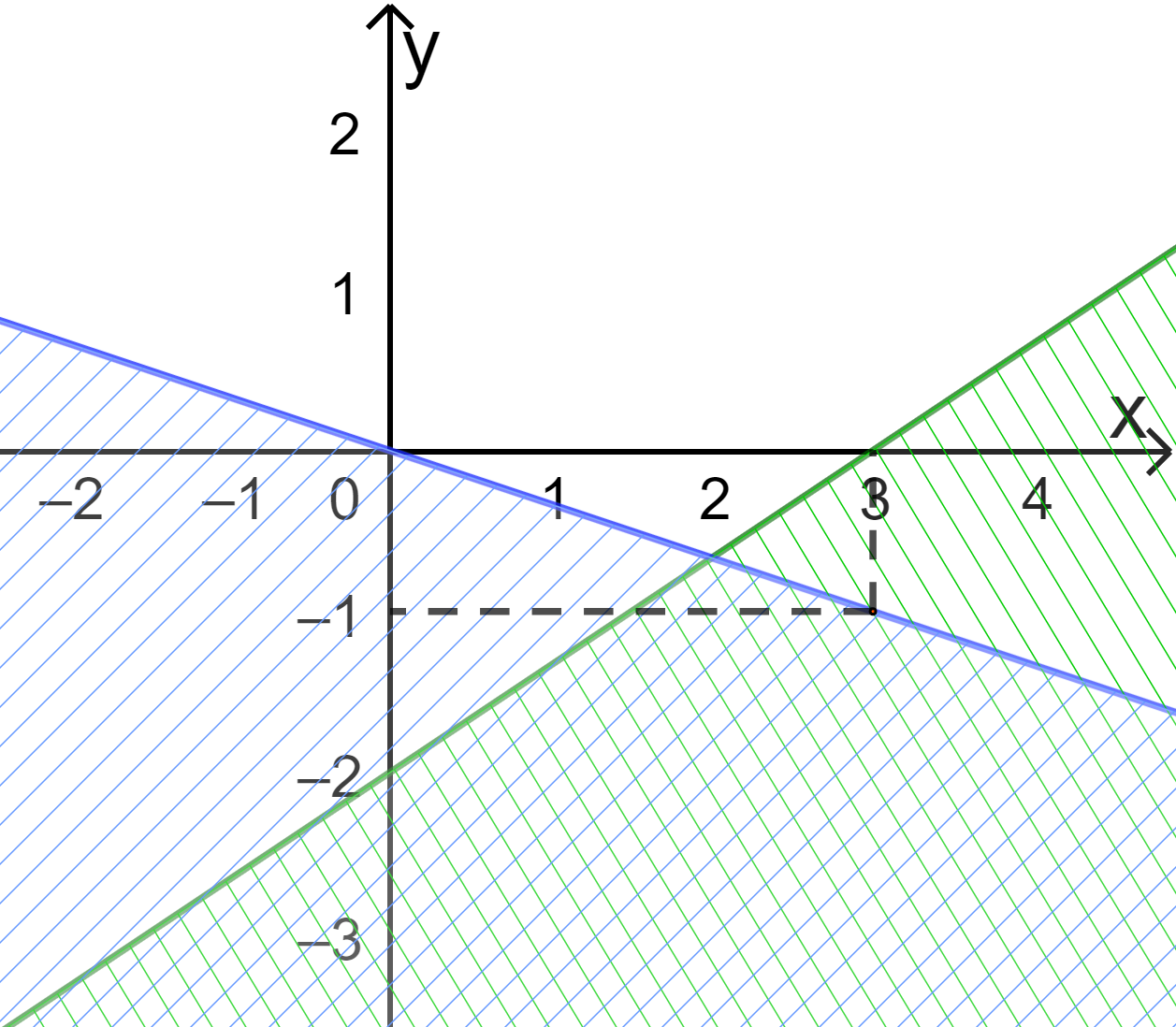
A. \(\left\{ \begin{array}{l}2x - 3y > 6\\x + 3y < 0\end{array} \right.\) B. \(\left\{ \begin{array}{l}2x - 3y < 6\\x + 3y > 0\end{array} \right.\) C. \(\left\{ \begin{array}{l}3x - 2y < 6\\x + 3y < 0\end{array} \right.\) D. \(\left\{ \begin{array}{l}2x - 3y > 6\\x - 3y > 0\end{array} \right.\)
Câu 23: Cho tam giác \(ABC\), có độ dài ba cạnh là \(BC = a,AC = b,AB = c\). Gọi \({m_a}\) là độ dài đường trung tuyến kẻ từ đỉnh \(A\), \(R\) là bán kính đường tròn ngoại tiếp tam giác và \(S\) là diện tích tam giác đó. Mệnh đề nào sau đây sai?
A. \(m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4}\). B. \({a^2} = {b^2} + {c^2} + 2bc\cos A\).
C. \(S = \frac{{abc}}{{4R}}\). D. \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Câu 24: Cho hình vuông \(ABCD\) cạnh bằng \(2.\) Điểm \(M\) nằm trên đoạn thẳng \(AC\) sao cho \(AM = \frac{{AC}}{4}\). Gọi \(N\) là trung điểm của đoạn thẳng \(DC.\) Tính \(\overrightarrow {MB} .\overrightarrow {MN} .\)
A. \(\overrightarrow {MB} .\overrightarrow {MN} = - 4.\) B. \(\overrightarrow {MB} .\overrightarrow {MN} = 0.\) C. \(\overrightarrow {MB} .\overrightarrow {MN} = 4.\) D. \(\overrightarrow {MB} .\overrightarrow {MN} = 16.\)
Câu 25: Kết quả đo chiều dài của một chiếc bàn được ghi là \(120cm \pm 0,5cm\), điều đó có nghĩa là:
A. Chiều dài đúng của chiếc bàn là một số nằm trong khoảng 119,5cm đến 120,5cm.
B. Chiều dài đúng của chiếc bàn là một số lớn hơn 120cm.
C. Chiều dài đúng của chiếc bàn là một số nhỏ hơn 120cm.
D. Chiều dài đúng của chiếc bàn là 119,5m hoặc là 120,5cm.
Câu 26: Một thửa ruộng hình chữ nhật có chiều dài là \(x = 23{\rm{m}} \pm 0,01{\rm{m}}\) và chiều rộng là \(y = 15{\rm{m}} \pm 0,01{\rm{m}}\). Tính diện tích \(S\) của thửa ruộng đã cho.
A. \(S = 345{\rm{m}} \pm 0,001{\rm{m}}{\rm{.}}\) B. \(S = 345{\rm{m}} \pm 0,38{\rm{m}}{\rm{.}}\)
C. \(S = 345{\rm{m}} \pm 0,01{\rm{m}}{\rm{.}}\) D. \(S = 345{\rm{m}} \pm 0,3801{\rm{m}}{\rm{.}}\)
Câu 27: Cho dãy số liệu thống kê: 5; 6; 7; 8; 9. Phương sai của dãy số liệu thống kê trên là:
A. 10 B. 7 C. 6 D. 2
Câu 28: Lớp 10A có 51 bạn học sinh trong đó có 31 bạn học tiếng Anh và 27 bạn học tiếng Nhật. Lớp 10A có bao nhiêu bạn học cả tiếng Anh và tiếng Nhật?
A. \(7\). B. \(9\). C. \(5\). D. \(12\).
Câu 29: Cho tam giác \(ABC\) đều cạnh \(a\). Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|.\)
A. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 .\) B. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \frac{{a\sqrt 3 }}{2}.\)
C. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2a.\) D. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2a\sqrt 3 .\)
Câu 30: Cho tam giác \(ABC\) và điểm \(M\) thỏa mãn \(\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {AB} \). Tìm vị trí điểm \(M.\)
A. \(M\) là trung điểm của \(AC.\) B. \(M\) là trung điểm của \(AB.\)
C. \(M\) là trung điểm của \(BC.\) D. \(M\) là điểm thứ tư của hình bình hành \(ABCM.\)
Phần 2: Tự luận (4 điểm)
Câu 1: Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ. Chứng minh rằng:
a) \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {IJ} \).
b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
c) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \) với M là điểm bất kỳ.
Câu 32: Cho các số liệu thống kê về sản lượng chè thu được trong 1 năm (kg/sào) của 20 hộ gia đình
|
111 |
112 |
112 |
113 |
114 |
114 |
115 |
114 |
115 |
116 |
|
112 |
113 |
113 |
114 |
115 |
114 |
116 |
117 |
113 |
115 |
a) Tính số trung bình và trung vị của mẫu số liệu trên.
b) Tính phương sai và độ lệch chuẩn
Câu 33: Từ một đỉnh tháp người ta nhìn hai điểm \(A\) và \(B\) trên mặt đất dưới các góc nhìn là \(\alpha = {72^0}12'\) và \(\beta = {34^0}26'\). Ba điểm \(A,B,C\) thẳng hàng trong đó C là điểm chính giữa chân tháp. Tính chiều cao CD của tháp biết \(AB = 91m\).
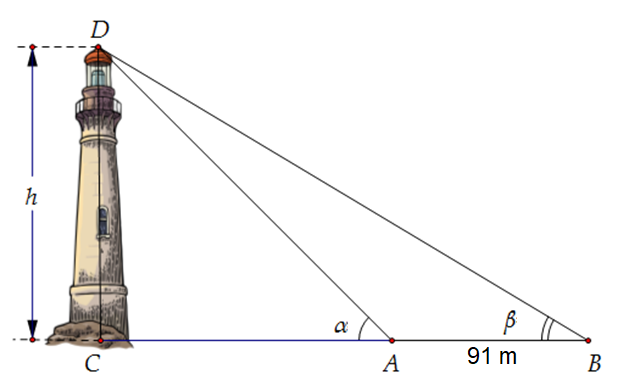
----- HẾT -----
Lời giải
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
|
1.D |
2.B |
3.D |
4.A |
5.A |
6.D |
7.B |
8.C |
9.D |
10.C |
|
11.B |
12.B |
13.D |
14.A |
15.D |
16.A |
17.A |
18.A |
19.D |
20.B |
|
21.C |
22.B |
23.B |
24.B |
25.A |
26.D |
27.D |
28.A |
29.A |
30.A |
Câu 1 (NB):
Phương pháp:
Mệnh đề là câu khẳng định có tính đúng hoặc sai.
Cách giải:
Phát biểu ở A, B, C là câu cảm thán và câu hỏi nên không là mệnh đề.
Chọn D.
Câu 2 (NB):
Cách giải:
Độ chính xác \(d = 101\) (hàng trăm), nên ta làm tròn số \(a = 23748023\)đến hàng nghìn, được kết quả là \(a = 23748000\).
Chọn B.
Câu 3 (TH):
Phương pháp:
Sử dụng quy tắc ba điểm.
Cách giải:
Xét các đáp án:
Đáp án A. Ta có \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0 .\)
Đáp án B. Ta có \(\overrightarrow {AP} + \overrightarrow {BM} + \overrightarrow {CN} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} + \frac{1}{2}\overrightarrow {CA} \)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} } \right) = \frac{1}{2}\overrightarrow {AA} = \overrightarrow 0 .\)
Đáp án C. Ta có \(\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PM} = \overrightarrow {MM} = \overrightarrow 0 .\)
Đáp án D. Ta có \(\overrightarrow {PB} + \overrightarrow {MC} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \frac{1}{2}\overrightarrow {AC} = \overrightarrow {AN} = \overrightarrow {PM} = - \overrightarrow {MP} .\)
Chọn D.
Câu 4 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \angle BAC.\)
Cách giải:
Do ABCD là hình thoi, có \(\widehat {BAD} = {60^ \circ } \Rightarrow \widehat {ABC} = {120^ \circ }\)
Theo định lí hàm cosin, ta có
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos A\\ = {1^2} + {1^2} - 2.1.1.\cos {120^ \circ } = 3 \Rightarrow AC = \sqrt 3 \end{array}\)
Chọn A.
Câu 5 (NB):
Phương pháp:
Cặp số nào không thỏa mãn bất phương trình thì không là nghiệm của bất phương trình.
Cách giải:
Thay cặp số (x;y) = (0;4) vào bất phương trình: 2.0 – 4 + 3 > 0 => Sai.
Thay cặp số (x;y) = (2;5) vào bất phương trình: 2.2 – 5 + 3 > 0 => Đúng.
Thay cặp số (x;y) = (1;3) vào bất phương trình: 2.1 – 3 + 3 > 0 => Đúng.
Thay cặp số (x;y) = (1;4) vào bất phương trình: 2.1 – 4 + 3 > 0 => Đúng.
Chọn A.
Câu 6 (TH):
Cách giải:
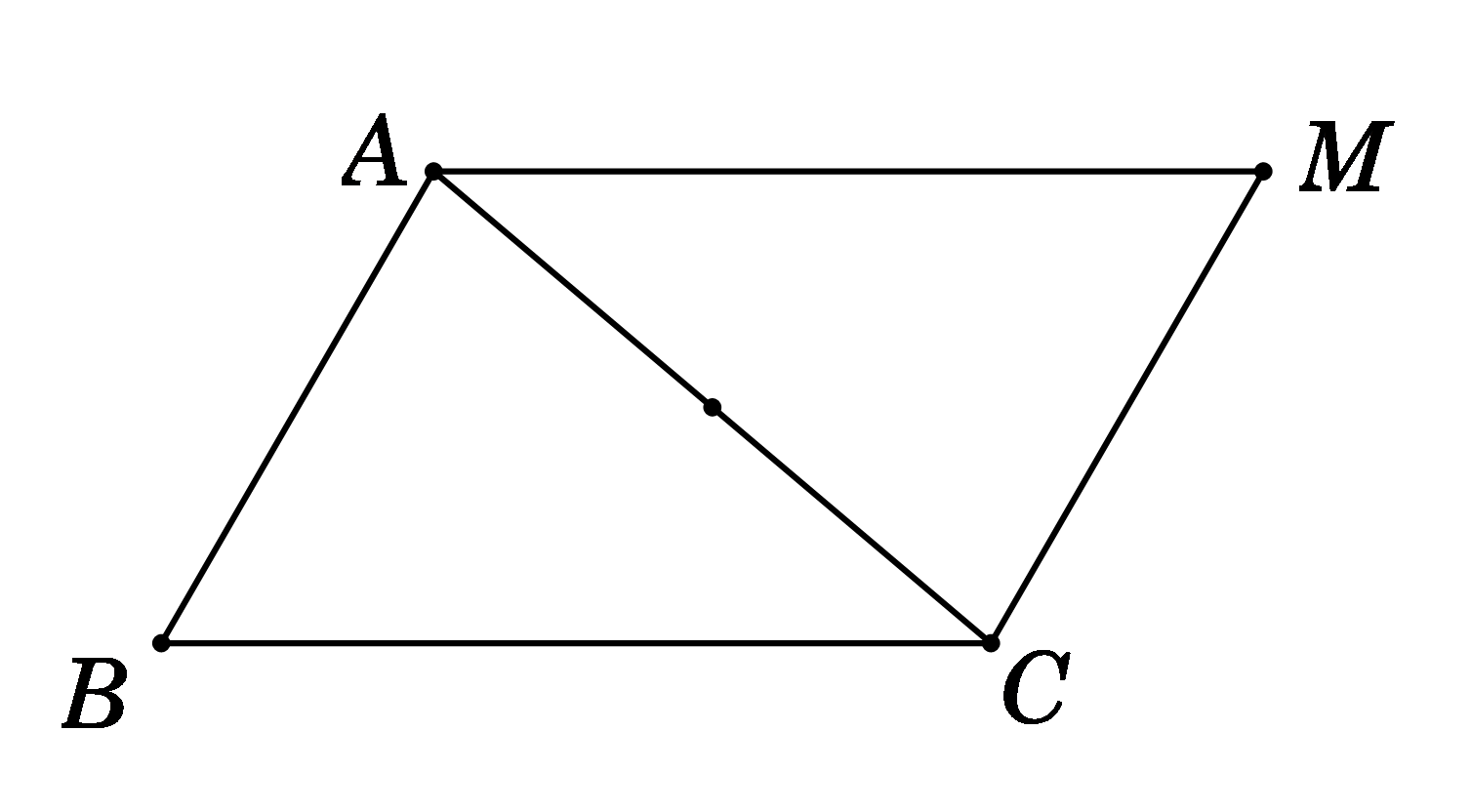
Ta có \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \)
\( \Rightarrow MABC\) là hình bình hành
\( \Rightarrow \overrightarrow {MA} = \overrightarrow {CB} .\)
Do đó D sai.
Chọn D.
Câu 7 (NB):
Phương pháp:
Áp dụng định lí cosin \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}\)
Cách giải:
Vì D là trung điểm của BC \( \Rightarrow A{D^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4} = 27 \Rightarrow AD = 3\sqrt 3 \)
Tam giác ABD có \(AB = BD = DA = 3\sqrt 3 \Rightarrow \)\(\Delta ABD\) đều.
Nên có bán kính đường tròn ngoại tiếp là \(\frac{{\sqrt 3 }}{3}AB = \frac{{\sqrt 3 }}{3}.3\sqrt 3 = 3\)
Chọn B.
Câu 8 (VD):
Cách giải:
Ta có \(|\vec a + \vec b{|^2} - |\vec a - \vec b{|^2} = {(\vec a + \vec b)^2} - {(\vec a - \vec b)^2} = 4\vec a\vec b \Rightarrow \vec a \cdot \vec b = \frac{1}{4}\left( {|\vec a + \vec b{|^2} - |\vec a - \vec b{|^2}} \right)\).
- A đúng, vì \(|\vec a + \vec b{|^2} = {(\vec a + \vec b)^2} = (\vec a + \vec b) \cdot (\vec a + \vec b) = \vec a \cdot \vec a + \vec a \cdot \vec b + \vec b \cdot \vec a + \vec b \cdot \vec b = |\vec a{|^2} + |\vec b{|^2} + 2\vec a \cdot \vec b\)
\( \Rightarrow \vec a \cdot \vec b = \frac{1}{2}\left( {|\vec a + \vec b{|^2} - |\vec a{|^2} - |\vec b{|^2}} \right)\)
- B đúng, vì \(|\vec a - \vec b{|^2} = {(\vec a - \vec b)^2} = (\vec a - \vec b) \cdot (\vec a - \vec b) = \vec a \cdot \vec a - \vec a \cdot \vec b - \vec b \cdot \vec a + \vec b \cdot \vec b = |\vec a{|^2} + |\vec b{|^2} - 2\vec a \cdot \vec b\)
\( \Rightarrow \vec a \cdot \vec b = \frac{1}{2}\left( {|\vec a{|^2} + |\vec b{|^2} - |\vec a - \vec b{|^2}} \right)\).
Chọn C.
Câu 9 (TH):
Cách giải:
Theo tính chất của hình thoi, hình chữ nhật và hình vuông, ta có:
\(C \subset A\) và \(C \subset B\) nên \(B\backslash A = C\), \(A\backslash B = C\) là các mệnh đề sai.
Vì hình vuông vừa là hình thoi và cũng là hình chữ nhật nên \(A \cap B = C\) là mệnh đề đúng và \(A \cup B = C\) là mệnh đề sai.
Chọn D.
Câu 10 (TH):
Phương pháp:
Sử dụng khái niệm các phép toán trên tập hợp.
Cách giải:
Gọi A là tập hợp học sinh được xếp loại học lực giỏi .
Gọi B là tập hợp học sinh được xếp loại hạnh kiểm tốt .
Khi đó \(A \cap B\) là tập hợp học sinh vừa được xếp loại học lực giỏi , vừa có hạnh kiểm tốt .
\(A \cup B\)là tập hợp học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt .
Ta có \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right) = 15 + 20 - 10 = 25\).
Chọn C.
Câu 11 (TH):
Phương pháp:
Sử dụng định lí Cosin trong tam giác ABC ta có: \(A{B^2} = A{C^2} + B{C^2} - 2AC.BC.\cos C.\)
Cách giải:
Ta có: Sau \(2h\) quãng đường tàu thứ nhất chạy được là: \({S_1} = 30.2 = 60\,km.\)
Sau \(2h\) quãng đường tàu thứ hai chạy được là: \({S_2} = 40.2 = 80\,km.\)
Vậy: sau \(2h\) hai tàu cách nhau là: \(S = \sqrt {{S_1}^2 + {S_2}^2 - 2{S_1}.{S_2}.\cos {{60}^0}} = 20\sqrt {13} .\)
Chọn B.
Câu 12 (TH):
Phương pháp:
Dùng công thức \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\) tính P theo \(\tan \alpha \)
Cách giải:
Vì \(\tan \alpha \) xác định nên \(\cos \alpha \ne 0\). Chia cả tử và mẫu của P cho \(\cos \alpha \) ta được:
\(P = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }} = \frac{{6\frac{{\sin \alpha }}{{\cos \alpha }} - 7}}{{6 + 7\frac{{\sin \alpha }}{{\cos \alpha }}}} = \frac{{6\tan \alpha - 7}}{{6 + 7\tan \alpha }} = \frac{{6.( - 3) - 7}}{{6 + 7.( - 3)}} = \frac{5}{3}\)
Chọn B.
Câu 13 (TH):
Phương pháp:
Xác định tập hợp A, B trên trục số.
Cách giải:
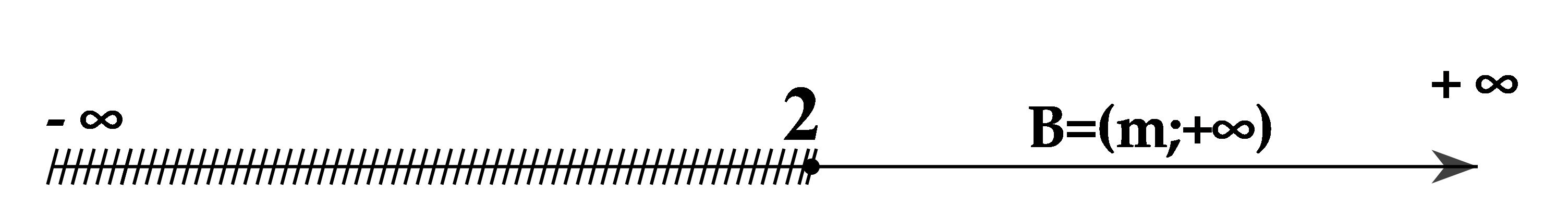
Ta có: \(B \subset A\) khi và chỉ khi \(\forall x \in B \Rightarrow x \in A\)\( \Rightarrow m \ge 2\).
Chọn D.
Câu 14 (TH):
Cách giải:
Từ giả thiết suy ra
Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được
Chọn A.
Câu 15 (TH):
Cách giải:
Ta có: \(\overrightarrow {AB} .\overrightarrow {BD} = \overrightarrow {AB} \left( {\overrightarrow {BA} + \overrightarrow {BC} } \right) = \overrightarrow {AB} .\overrightarrow {BA} + \overrightarrow {AB} .\overrightarrow {BC} = - \overrightarrow {AB} .\overrightarrow {AB} + \overrightarrow 0 = - A{B^2} = - 64.\)
Chọn D.
Câu 16 (TH):
Cách giải:
Ta có \(AB = \sqrt 2 \Rightarrow AC = CB = 1.\)
Gọi \(I\) là trung điểm \(BC \Rightarrow AI = \sqrt {A{C^2} + C{I^2}} = \frac{{\sqrt 5 }}{2}.\)
Khi đó
\(\overrightarrow {AC} + \overrightarrow {AB} = 2\overrightarrow {AI} \Rightarrow \left| {\overrightarrow {AC} + \overrightarrow {AB} } \right| = 2\left| {\overrightarrow {AI} } \right| = 2.\frac{{\sqrt 5 }}{2} = \sqrt 5 .\)
Chọn A.
Câu 17 (NB):
Cách giải:
Tiền thưởng 4 triệu đồng được thưởng cho 15 người \( \Rightarrow {M_0} = 4\)
Chọn A.
Câu 18 (NB):
Phương pháp:
Cho mẫu số liệu có kích thước \(N\) là \(\left\{ {{x_1};{\mkern 1mu} {\mkern 1mu} {x_2};{\mkern 1mu} {\mkern 1mu} \ldots ;{\mkern 1mu} {\mkern 1mu} {x_N}} \right\}\). Phương sai của mẫu số liệu này bằng trung bình của tổng các bình phương độ lệch giữa các giá trị với số trung bình.
Cách giải:
Dựa theo lý thuyết, ta có:
Dãy số liệu \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}, \ldots ,{\mkern 1mu} {\mkern 1mu} {x_N}\) có kích thước mẫu \(N\), phương sai được tính theo công thức:
\({s^2} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} - \bar x} \right)}^2}} \) trong đó \(\bar x = \) trung bình cộng của mẫu số liệu
Chọn A.
Câu 19 (TH):
Phương pháp:
Sử dụng hệ quả của định lí cosin \(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)
Cách giải:
Ta có \(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)\( = \frac{{{4^2} + {9^2} - {7^2}}}{{2.4.9}} = \frac{2}{3}\).
Chọn D.
Câu 20 (TH):
Phương pháp:
Đối với bảng phân bố tần số ghép lớp:
+ Số trung bình cộng: \(\bar x = \frac{{{c_1}{n_1} + {c_2}{n_2} + \ldots + {c_k}{n_k}}}{N}\)
+ Phương sai: \({s^2} = \frac{1}{N}\left[ {{n_1}{{\left( {{c_1} - \bar x} \right)}^2} + {n_2}{{\left( {{c_2} - \bar x} \right)}^2} + \ldots + {n_k}{{\left( {{c_k} - \bar x} \right)}^2}} \right]\)
+ Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)
Với \({n_i}\) là tần số của giá trị \({c_i}\).
Cách giải:
Ta có bảng phân bố tần số, tần suất ghép lớp:
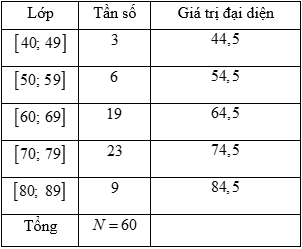
Số trung bình cộng:
\(\bar x = \frac{{44,5.3 + 54,5.6 + 64,5.19 + 74,5.23 + 84,5.9}}{{60}} = \frac{{4160}}{{60}} \approx 69,33\) (nghìn đồng)
Phương sai:
\({s^2} = \frac{1}{{60}}\left( {3.44,{5^2} + 6.54,{5^2} + 19.64,{5^2} + 23.74,{5^2} + 9.84,{5^2}} \right) - {\left( {\frac{{4160}}{{60}}} \right)^2}\)\( = \frac{{3779}}{{36}}\) (nghìn đồng)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)\( = \sqrt {\frac{{3779}}{{36}}} {\rm{\;}} \approx 10,25\) (nghìn đồng)
Chọn B.
Câu 21 (NB):
Cách giải:
Ta có \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) - y + 3\, \Leftrightarrow \, - x + 3y - 1 > 0\).
Vì \( - 2 + 3.1 - 1 > 0\) là mệnh đề đúng nên miền nghiệm của bất phương trình trên chứa điểm có tọa độ \(B\).
Chọn C.
Câu 22 (VD):
Phương pháp:
Xác định các đường thẳng và bất phương trình tương ứng, kết hợp loại nghiệm.
Cách giải:
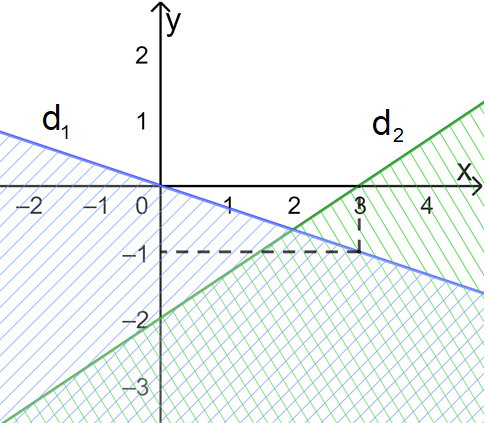
Kí hiệu hai đường thẳng trên hình lần lượt là \({d_1},{d_2}\)
\({d_1}\) đi qua \(O(0;0)\) và \(A(3; - 1)\), suy ra \({d_1}:x + 3y = 0\) (Loại D)
\({d_2}\) đi qua \((3;0)\) và \((0; - 2)\), suy ra \({d_2}:2x - 3y = 6\) (Loại C)
Điểm \((0,1)\) thuộc miền nghiệm, mà 2.0 – 3.1= -3 <6 => BPT \(2x - 3y < 6\) (Loại A)
Chọn B.
Câu 23 (NB):
Cách giải:
Theo định lý cosin trong tam giác ta có \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Chọn B.
Câu 24 (TH):
Phương pháp:
Sử dụng công thức \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = BM.BA.\cos \left( {\overrightarrow {BM} ,\overrightarrow {BA} } \right).\)
Cách giải:
Giả thiết không cho góc, ta phân tích các vectơ \(\overrightarrow {MB} ,\overrightarrow {MN} \) theo các vectơ có giá vuông góc với nhau.
\(\overrightarrow {MB} = \overrightarrow {AB} - \overrightarrow {AM} = \overrightarrow {AB} - \frac{1}{4}\overrightarrow {AC} = \overrightarrow {AB} - \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \frac{3}{4}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AD} \)
\(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \overrightarrow {AD} + \overrightarrow {DN} - \frac{1}{4}\overrightarrow {AC} = \overrightarrow {AD} + \frac{1}{2}\overrightarrow {DC} - \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\)
\(\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} - \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AD} \).
\(\begin{array}{l} \Rightarrow \overrightarrow {MB} .\overrightarrow {MN} = \left( {\frac{3}{4}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AD} } \right).\left( {\frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AD} } \right)\\ = \frac{1}{{16}}\left( {3\overrightarrow {AB} - \overrightarrow {AD} } \right)\left( {\overrightarrow {AB} + 3\overrightarrow {AD} } \right)\\ = \frac{1}{{16}}\left( {3A{B^2} + 8\overrightarrow {AB} .\overrightarrow {AD} - 3A{D^2}} \right)\\ = \frac{1}{{16}}\left( {3{a^2} + 8.0 - 3{a^2}} \right) = 0\end{array}\) .
Chọn B.
Câu 25 (NB):
Phương pháp:
Xác định số gần đúng a và độ chính xác d.
Tính số đúng \(\bar a = a \pm d \Rightarrow a - d \le \bar a \le a + d\).
Cách giải:
Gọi \(\bar a\) là chiều dài đúng của chiếc bàn \( \Rightarrow \bar a = 120cm \pm 0,5cm\).
\(\begin{array}{*{20}{l}}{ \Rightarrow 120 - 0,5 \le \bar a \le 120 + 0,5}\\{ \Leftrightarrow 119,5 \le \bar a \le 120,5}\end{array}\)
Vậy chiều dài đúng của chiếc bàn là một số nằm trong khoảng 119,5cm đến 120,5cm.
Chọn A.
Câu 26 (TH):
Cách giải:
Diện tích của thửa ruộng là
\(S = xy = \left( {23 \pm 0,01} \right).\left( {15 \pm 0,01} \right)\)
\( = 23.15 \pm \left( {23.0,01 + 15.0,01 + 0,{{01}^2}} \right) = 345 \pm 0,3801.\)
Chọn D.
Câu 27 (TH):
Cách giải:
+ Trung bình cộng của dãy là \(\overline x = 7\)
+ Phương sai của dãy số liệu thống kê là:
\({S^2} = \frac{{1{{\left( {5 - 7} \right)}^2} + 1.{{\left( {6 - 7} \right)}^2} + 1.{{\left( {7 - 7} \right)}^2} + 1.{{\left( {8 - 7} \right)}^2} + 1.{{\left( {9 - 7} \right)}^2}}}{5}\) \({S^2} = \frac{{10}}{5} = 2\)
Chọn D.
Câu 28 (TH):
Cách giải:
Số học sinh học cả tiếng Anh và tiếng Nhật của lớp 10A là \(31 + 27 - 51 = 7\) bạn.
Chọn A.
Câu 29 (TH):
Phương pháp:
Sử dụng tính chất trung điểm.
Cách giải:
Gọi \(H\) là trung điểm của \(BC \Rightarrow AH \bot BC.\)
Suy ra \(AH = \frac{{BC\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}.\)
Ta lại có \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AH} } \right| = 2.\frac{{a\sqrt 3 }}{2} = a\sqrt 3 .\)
Chọn A.
Câu 30 (TH):
Cách giải:
Gọi \(I\) là trung điểm của \(BC \Rightarrow \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MI} \)
\( \Leftrightarrow \overrightarrow {AB} = 2\overrightarrow {MI} \) \( \Rightarrow MI//AB,MI = \frac{1}{2}AB\)
Suy ra M là trung điểm \(AC.\)
Chọn A.
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
Phương pháp:
Sử dụng quy tắc ba điểm, công thức trung điểm.
Cách giải:
a) Theo quy tắc ba điểm ta có \(\overrightarrow {AC} = \overrightarrow {AI} + \overrightarrow {IC} = \overrightarrow {AI} + \overrightarrow {IJ} + \overrightarrow {JC} \)
Tương tự, ta có \(\overrightarrow {BD} = \overrightarrow {BI} + \overrightarrow {IJ} + \overrightarrow {JD} \)
Mà I, J lần lượt là trun điểm của AB và CD nên \(\overrightarrow {AI} + \overrightarrow {IB} = \overrightarrow 0 ,\overrightarrow {CJ} + \overrightarrow {JD} = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {AC} + \overrightarrow {BD} = \left( {\overrightarrow {AI} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {CJ} + \overrightarrow {JD} } \right) + 2\overrightarrow {IJ} = \overrightarrow 0 + \overrightarrow 0 + 2\overrightarrow {IJ} = 2\overrightarrow {IJ} \)
b) Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OI} \), \(\overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {OJ} \) (Do I, J là trung điểm AB, CD)
và \(\overrightarrow {OI} + \overrightarrow {OJ} = \overrightarrow 0 \) (do O là trung điểm IJ)
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {OJ} + 2\overrightarrow {OI} = 2\left( {\overrightarrow {OI} + \overrightarrow {OJ} } \right) = \overrightarrow 0 \)
c) Theo câu b) ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
\(\begin{array}{l} \Rightarrow \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right)\\ = 4\overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 4\overrightarrow {MO} + \overrightarrow 0 = 4\overrightarrow {MO} \end{array}\)
Câu 2 (VD): Cho các số liệu thống kê về sản lượng chè thu được trong 1 năm (kg/sào) của 20 hộ gia đình
|
111 |
112 |
112 |
113 |
114 |
114 |
115 |
114 |
115 |
116 |
|
112 |
113 |
113 |
114 |
115 |
114 |
116 |
117 |
113 |
115 |
a) Tính số trung bình và trung vị của mẫu số liệu trên.
b) Tính phương sai và độ lệch chuẩn
Phương pháp:
a)
* Số trung bình của mẫu số liệu \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2},{\mkern 1mu} {\mkern 1mu} ....,{\mkern 1mu} {\mkern 1mu} {x_n}\) kí hiệu là \(\bar x\), được tính bằng công thức:
\(\bar x = \frac{{{x_2} + {x_2} + ... + {x_k}}}{n}\)
* Tìm trung vị của mẫu số liệu.
Để tìm trung vị của mẫu số liệu, ta thực hiện như sau:
- Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.
- Nếu giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.
b) Phương sai \({s^2} = \frac{1}{n}\left( {{n_1}x_1^2 + {n_2}x_2^2 + ... + {n_k}x_k^2} \right) - {\overline x ^2}\)
Độ lệch chuẩn \(s = \sqrt {{s^2}} \)
Cách giải:
Bảng tần số
|
Giá trị |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
|
Tần số |
1 |
3 |
4 |
5 |
4 |
2 |
1 |
a)
* Số trung bình của mẫu số liệu trên là:
\(\bar x{\rm{ \;}} = \frac{{111.1 + 112.3 + 113.4 + 114.5 + 115.4 + 116.2 + 117.1}}{{20}} = 113,9\).
* Sắp xếp dãy số liệu theo thứ tự không giảm ta được:
111 112 112 112 113 113 113 113 114 114 114 114 114 115 115 115 115 116 116 117
Cỡ mẫu là n = 20 chẵn nên số trung vị là \({M_e} = \frac{1}{2}(114 + 114) = 114\).
b) Phương sai \({s^2} = \frac{1}{{20}}\left( {{{1.111}^2} + {{3.112}^2} + ... + {{1.117}^2}} \right) - 113,{9^2} = 2,29\)
Độ lệch chuẩn \(s = \sqrt {2,29} \approx 1,513\)
Câu 3 (VD):
Cách giải:
Ta có: \(\widehat {DAB} = {180^ \circ } - \alpha = {180^ \circ } - {72^ \circ }12' = {107^ \circ }48'\); \(\widehat {ADB} = \widehat {DAC} - \widehat {DBA} = \alpha - \beta = {72^ \circ }12' - {34^ \circ }26' = {37^ \circ }46'\)
Áp dụng định lí sin trong tam giác DAB ta có:
\(\begin{array}{l}\frac{{AB}}{{\sin D}} = \frac{{DB}}{{\sin A}} \Leftrightarrow \frac{{91}}{{\sin {{37}^ \circ }46'}} = \frac{{DB}}{{\sin {{107}^ \circ }48'}}\\ \Rightarrow DB = \sin {107^ \circ }48'.\frac{{91}}{{\sin {{37}^ \circ }46'}}\end{array}\)
Lại có: tam giác DCB vuông tại C, suy ra \(CD = \sin B.DB\)
\( \Rightarrow CD = \sin {34^ \circ }26'.DB = \sin {34^ \circ }26'.\sin {107^ \circ }48'.\frac{{91}}{{\sin {{37}^ \circ }46'}} \approx 80\)
Vậy tháp đó cao khoảng 80m.
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 7 timdapan.com"