Đề số 4 – Đề kiểm tra học kì 2 – Toán 9

Đề bài

Bài I (2,0 điểm): Cho hai biểu thức \(A = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}}\) và \(B = \left( {\dfrac{1}{{\sqrt x  - 1}} + \dfrac{{\sqrt x }}{{x - 1}}} \right).\dfrac{{x - \sqrt x }}{{2\sqrt x  + 1}}\) với \(x \ge 0\) và \(x \ne 1\)

1) Tính giá trị của A khi \(x = \dfrac{9}{4}\)

2) Rút gọn B

3) Với \(x \in \mathbb{N}\) và \(x \ne 1\), hãy tìm giá trị lớn nhất của biểu thức \(P = A.B\)

Bài II (2,0 điểm): Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Nhà bạn Mai có một mảnh vườn, được chia thành nhiều luống, mỗi luống trồng số lượng cây bắp cải như nhau. Mai tính rằng nếu tăng thêm 7 luống nhưng mỗi luống trồng ít đi 2 cây thì số lượng cây bắp cải toàn vườn giảm 9 cây; còn nếu giảm đi 5 luống nhưng mỗi luống trồng tăng thêm 2 cây thì số cải bắp cải toàn vườn sẽ tăng thêm 15 cây. Hỏi vườn nhà Mai hiện trồng tổng cộng bao nhiêu cây bắp cải?

Bài III (2,0 điểm):

1) Giải hệ phương trình \(\left\{ \begin{array}{l}\dfrac{9}{{\sqrt {2x - 1} }} - \dfrac{3}{{y + 1}} = 2\\\dfrac{4}{{\sqrt {2x - 1} }} - \dfrac{1}{{y + 1}} = 1\end{array} \right.\)

2) Cho đường thẳng \(d:y = 2x + {m^2} - 1\) và parabol \(\left( P \right):y = {x^2}\) (với m là tham số) trong mặt phẳng tọa độ Oxy

a) Tìm m để d cắt (P) tại hai điểm phân biệt A và B

Gọi H và K lần lượt là hình chiếu vuông góc của A và B trên trục hoành.Tìm m để độ dài đoạn thẳngHK bằng 3 (đơn vị độ dài)

Bài IV (3,5 điểm): Cho nửa đường tròn (O) đường kính \(AB = 2R;\) C là điểm bất kì nằm trên nửa đường tròn sao cho C khác A và \(AC < CB.\) Điểm D thuộc cung nhỏ BC sao cho \(\widehat {COD} = {90^0}.\) Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.

1) Chứng minh CEDF là tứ giác nội tiếp

2) Chứng minh FC.FA = FD.FB

3) Gọi I là trung điểm của EF. Chứng minh IC là tiếp tuyến của (O)

4) Hỏi khi C thay đổi thỏa mãn điều kiện bài toán, E thuộc đường tròn cố định nào?

Bài V (0,5 điểm): Cho hai số thực dương x và y thỏa mãn \(\dfrac{x}{2} + \dfrac{y}{8} \le 2.\) Tìm giá trị nhỏ nhất của biểu thức \(K = \dfrac{x}{y} + \dfrac{{2y}}{x}\)

Lời giải chi tiết

Bài I:

1) Tính giá trị của A

Thay \(x = \dfrac{9}{4}\) (TMĐK: \(x \ge 0\) và \(x \ne 1\)) vào A ta được \(A = \dfrac{{\sqrt {\dfrac{9}{4}}  + 1}}{{\sqrt {\dfrac{9}{4}}  - 1}}\)

Tìm được A = 5 và kết luận

2) Rút gọn B

Biến đổi \(B = \dfrac{{\sqrt x  + 1 + \sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\)\(\,.\dfrac{{\sqrt x \left( {\sqrt x  - 1} \right)}}{{2\sqrt x  + 1}}\)

Tìm được \(B = \dfrac{{\sqrt x }}{{\sqrt x  + 1}}\) và kết luận

3) Tìm giá trị lớn nhất của P

Tìm được \(P = \dfrac{{\sqrt x }}{{\sqrt x  - 1}} = 1 + \dfrac{1}{{\sqrt x  - 1}}\)

Tìm được \({P_{max}} = 2 + \sqrt 2 \) tại x = 2 và kết luận

Bài II:

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Gọi số luống ban đầu là a (luống, a > 5) và số cây bắp cải trồng mỗi luống ban đầu là b (cây, x > 2)

Số bắp cải trong vườn nhà Mai là ab (cây)

Vì khi tăng thêm 7 luốn và mỗi luống trồng ít đi 2 cây thì số cây bắp cải trong vườn giảm 9 cây nên ta có:

\(\left( {a + 7} \right)\left( {b - 2} \right) = ab - 9\)

Vì giảm đi 5 luống và mỗi luống trồng tăng thêm 2 cây thì số cải bắp cải toàn vườn sẽ tăng thêm 15 cây nên ta có:

\(\left( {a - 5} \right)\left( {b + 2} \right) = ab + 15\)

Ta có hệ phương trình: \(\left\{ \begin{array}{l}\left( {a + 7} \right)\left( {b - 2} \right) = ab - 9\\\left( {a - 5} \right)\left( {b + 2} \right) = ab + 15\end{array} \right.\)

Giải hệ ta được \(\left\{ \begin{array}{l}a = 50\\b = 15\end{array} \right.\) và kết luận

Bài III:

1) Giải hệ phương trình

ĐKXĐ: \(x \ge \dfrac{1}{2};y =  - 1\)

Đặt \(\dfrac{1}{{\sqrt {2x - 1} }} = a;\dfrac{1}{{y + 1}} = b,\) ta có: \(\left\{ \begin{array}{l}9a - 3b = 2\\4a - b = 1\end{array} \right.\)

Giải ra được \(a = b = \dfrac{1}{3}\)

Từ đó tìm được \(\left\{ \begin{array}{l}x = 5\\y = 2\end{array} \right.\) và kết luận

2) Đường thẳng và parabol

a) Tìm m để d cắt (P) tại hai điểm phân biệt

Phương trình hoành độ giao điểm của d và (P):

\({x^2} - 2x - \left( {{m^2} - 1} \right) = 0\)

d và (P) cắt nhau tại hai điểm phân biệt \( \Leftrightarrow \Delta ' > 0\)

Tìm được \(m \ne 0\) và kết luận

b) Tìm m để HK bằng 3

Gọi \({x_1},\) \({x_2}\) là các nghiệm của phương trình hoành độ giao điểm

Ta có: \(HK = \left| {{x_1} - {x_2}} \right| = 3\) nên \({\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 9\) với \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = 1 - {m^2}\end{array} \right.\)

Tìm được \(m =  \pm \dfrac{3}{2}\) và kết luận

Lưu ý:

- Học sinh có thể sử dụng công thức nghiệm để tìm được \({x_1} = 1 - m\) và \({x_2} = 1 + m\)

Bài IV:

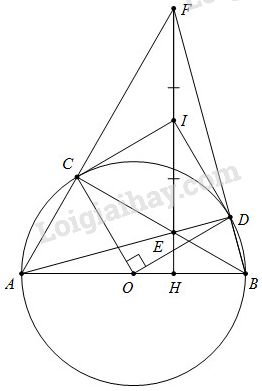
1) Chứng minh CEDF là tứ giác nội tiếp

Ta có: \(\widehat {ACB} = \widehat {ADB} = {90^0}\)

\( \Rightarrow \widehat {FCE} = \widehat {FDE} = {90^0}\)

Tứ giác CEDF có:

\( \Rightarrow \widehat {FCE} + \widehat {FDE} = {180^0}\)

Lập luận và kết luận

2) Chứng minh FC.FA = FD.BF

Xét \(\Delta FCB\) và \(\Delta FDA\) có \(\widehat {FCB} = \widehat {FDA} = {90^0}\) và \(\widehat {CFB}\) chung

\( \Rightarrow \Delta FCB\) # \(\Delta FDA\) (g - g)

\(\begin{array}{l} \Rightarrow \dfrac{{FC}}{{FD}} = \dfrac{{FB}}{{FA}}\\ \Rightarrow FC.FA = FD = FB\end{array}\)

3) Chứng minh IC tiếp xúc với (O)

\(\Delta OCA\) cân tại O nên \(\widehat {ICF} = \widehat {IFC}\)

\(\Delta ICF\) cân tại I nên \(\widehat {OAC} = \widehat {OCA}\)

Từ đó \(\widehat {ICF} + \widehat {OCA} = \widehat {IFC} + \widehat {OAC} = {90^0}\) Vì \(\Delta HAF\) vuông tại H (do E là trực tâm \(\Delta FAB\))

\( \Rightarrow \widehat {ICO} = {90^0} \Rightarrow IC \bot OC\)

Kết hợp với \(C \in \left( O \right)\) suy ra IC tiếp xúc với (O)

4) Khi C thay đổi E thuộc đường tròn cố định nào?

Gọi T là điểm chính giữa của cung AB không chứa C (T cố định)

IETO là hình bình hành (Vì IE song song và bằng OT)

\( \Rightarrow TE = OI = R\sqrt 2 \) (Vì ICOD là hình vuông cạnh E)

Vậy E thuộc \(\left( {T;R\sqrt 2 } \right)\)

Câu IV:

Tìm giá trị nhỏ nhất của K

Áp dụng bất đẳng thức Cauchy

\(2 \ge \dfrac{x}{2} + \dfrac{8}{y} \ge 2\sqrt {\dfrac{x}{2}.\dfrac{8}{y}}  = 4\sqrt {\dfrac{x}{y}}  \) \(\Rightarrow 0 < t = \dfrac{x}{y} \le \dfrac{1}{4}\)

Ta có: \(K = t + \dfrac{2}{t} = \left( {32t + \dfrac{2}{t}} \right) - 31t \)\(\,\ge 2\sqrt {32t.\dfrac{2}{t}}  - 31.\dfrac{1}{4} = \dfrac{{33}}{4}\)

Dáu "=" xảy ra\( \Leftrightarrow t = \dfrac{1}{4}\) hay \(x = 2;y = 8\)

Vậy \({K_{\min }} = \dfrac{{33}}{4} \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 8\end{array} \right.\)