Đề số 2 – Đề kiểm tra học kì 2 – Toán 9

Đề bài

Bài I (2,0 điểm) Cho hai biểu thức  \(A = \dfrac{{\sqrt x  + 2}}{{1 + \sqrt x }}\)và \(B = \left( {\dfrac{{2\sqrt x }}{{x - \sqrt x  - 6}} + \dfrac{{\sqrt x }}{{\sqrt x  - 3}}} \right)\)\(\,:\dfrac{{\sqrt x }}{{\sqrt x  - 3}}\)

   với  \(x > 0,x \ne 9.\)

1) Tính giá trị biểu thức \(A\) khi \(x = 36.\)

2) Rút gọn biểu thức  \(B.\)

3) Với \(x \in {\bf{Z}},\) tìm giá trị lớn nhất của biểu thức \(P = AB.\)

Bài II (2,0 điểm). Giải bài toán sau bằng cách lập hệ phương trình:           

Theo kế hoạch, hai xí nghiệp A và B phải làm tổng cộng 720 dụng cụ cùng loại. Trên thực tế do cải tiến kĩ thuật, xí nghiệp A hoàn thành vượt mức 12%, còn xí nghiệp B hoàn thành vượt mức 10% so với kế hoạch. Do đó thực tế cả hai xí nghiệp làm được tổng cộng 800 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm theo kế hoạch?

Bài III (2,0 điểm)

1) Giải phương trình :   \(3{x^4} - 2{x^2} - 40 = 0\)

2) Cho phương trình \({x^2} + \left( {m - 1} \right)x - {m^2} - 2 = 0\,\,\,\,(1),\) với \(m\) là tham số thực.

 a) Chứng minh: phương trình (1) luôn có hai nghiệm trái dấu \({x_1},{x_2}\) với mọi giá trị của \(m\).

 b) Tìm \(m\) để biểu thức \(T = {\left( {\dfrac{{{x_1}}}{{{x_2}}}} \right)^3} + {\left( {\dfrac{{{x_2}}}{{{x_1}}}} \right)^3}\) đạt giá trị lớn nhất.

Bài IV (3,5 điểm).

Cho tam giác \(ABC\) nhọn, nội tiếp đường tròn \(\left( O \right).\) Ba đường cao \(AD,\,BE,\,CF\) của tam giác \(ABC\) cùng đi qua trực tâm \(H.\)

1) Chứng minh: Tứ giác \(BFEC\) nội tiếp.

2) Kẻ đường kính \(AK\) của đường tròn \(\left( O \right).\)

Chứng minh: tam giác \(ABD\) đồng dạng với tam giác \(AKC\) và \(AB.AC = 2AD.R.\)

3) Gọi \(M\) là hình chiếu vuông góc của \(C\) trên \(AK.\) Chứng minh: \(MD\) song song với \(BK.\)

4) Giả sử \(BC\) là dây cố định của đường tròn \(\left( O \right)\) còn \(A\) di động trên cung lớn \(BC.\) Tìm vị trí     của điểm \(A\) để diện tích tam giác \(AEH\) lớn nhất.

Bài V (0,5 điểm).

Cho \(a,b,c\) là các số thực dương thỏa mãn: \(ab + bc + ac = 3abc.\)Tìm giá trị nhỏ nhất của biểu thức:

\(K = \dfrac{{{a^2}}}{{c\left( {{c^2} + {a^2}} \right)}} + \dfrac{{{b^2}}}{{a\left( {{a^2} + {b^2}} \right)}} \)\(\,+ \dfrac{{{c^2}}}{{b\left( {{b^2} + {c^2}} \right)}}\,.\)

Lời giải chi tiết

Bài I:

1) \(x = 36\,\,({\rm{tmdk}}) \Rightarrow \sqrt x  = 6\)

\(A = \dfrac{{\sqrt x  + 2}}{{1 + \sqrt x }} = \dfrac{{6 + 2}}{{1 + 6}} = \dfrac{8}{7}\) khi \(x = 36\)

2) 

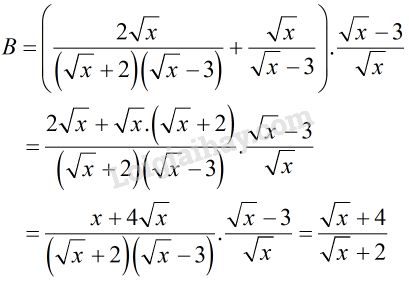
3) \(P = A.B = \dfrac{{\sqrt x  + 2}}{{\sqrt x  + 1}}\dfrac{{\sqrt x  + 4}}{{\sqrt x  + 2}}\)\(\, = \dfrac{{\sqrt x  + 4}}{{\sqrt x  + 1}} = 1 + \dfrac{3}{{\sqrt x  + 1}}\)

\(\begin{array}{l}x > 0;x \in \mathbb{Z} \Rightarrow x \ge 1\,\,\, \Rightarrow \sqrt x  \ge 1\\ \Rightarrow \sqrt x  + 1 \ge 2\\ \Rightarrow \dfrac{3}{{\sqrt x  + 1}} \le \dfrac{3}{2}\\ \Rightarrow P = 1 + \dfrac{3}{{\sqrt x  + 1}} \le \dfrac{5}{2}\end{array}\)

\(\max P = \dfrac{5}{2}\,\,{\rm{khi}}\,x = 1\)

Bài II: Gọi số dụng cụ mỗi xí nghiệp A và B phải làm theo kế hoạch lần lượt là \(x,\,y\) (dụng cụ, \(x,y \in {\mathbb{N}^ * },x,y < 120\))

Vì theo kế hoạch, hai xí nghiệp A và B phải làm tổng cộng 720 dụng cụ cùng loại nên: \(x + y = 720\)

Trên thực tế do cải tiến kĩ thuật, xí nghiệp A hoàn thành vượt mức 12%, còn xí nghiệp B hoàn thành vượt mức 10% so với kế hoạch.

 Do đó thực tế cả hai xí nghiệp làm được:\(1,12x + 1,1y\) dụng cụ

 Vậy \(1,12x + 1,1y = 800\)

Giải hệ phương trình \(\left\{ \begin{array}{l}x + y = 720\\1,12x + 1,1y = 800\end{array} \right.\)

ta được \(\left\{ \begin{array}{l}x = 400\\y = 320\end{array} \right.\) và kết luận.

Bài III:

1)

\(\begin{array}{l}3{x^4} - 2{x^2} - 40 = 0\\ \Leftrightarrow 3{x^4} - 12{x^2} + 10{x^2} - 40 = 0\\ \Leftrightarrow \left( {{x^2} - 4} \right)\left( {3{x^2} + 10} \right) = 0\\ \Leftrightarrow {x^2} - 4 = 0 \\\Leftrightarrow x =  \pm 2\end{array}\)

(Do \(3{x^2} + 10 > 0\)). Vậy \(S = \left\{ { \pm 2} \right\}\)

2)

a) Phương trình \({x^2} + \left( {m - 1} \right)x - {m^2} - 2 = 0\,\,\,\) là phương trình bậc hai có hệ số \(a.c =  - {m^2} - 2 < 0\,\,\forall m\)  nên luôn có hai nghiệm phân biệt trái dấu \({x_1},{x_2}\) với mọi giá trị của \(m\).

b) Theo định lí Vi ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1 - m\\{x_1}{x_2} =  - {m^2} - 2\end{array} \right.\)

Đặt \(t = \dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}}\) thì \(t = \dfrac{{x_1^2 + x_2^2}}{{{x_1}{x_2}}} \)\(\,= \dfrac{{{{({x_1} + {x_2})}^2}}}{{{x_1}{x_2}}} - 2 \)\(\,= \dfrac{{{{(1 - m)}^2}}}{{ - {m^2} - 2}} - 2 \le  - 2\,\forall m\)

\(T = {\left( {\dfrac{{{x_1}}}{{{x_2}}}} \right)^3} + {\left( {\dfrac{{{x_2}}}{{{x_1}}}} \right)^3} \)\(\,= {\left( {\dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}}} \right)^3} - 3.\left( {\dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}}} \right) \)\(\,= {t^3} - 3t = t({t^2} - 3)\)

\(\left. \begin{array}{l}t \le  - 2 \Rightarrow {t^2} \ge 4 \Rightarrow ({t^2} - 3) \ge 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - t \ge 2\end{array} \right\} \)\(\,\Rightarrow  - t({t^2} - 3) \ge 2 \Rightarrow T \le  - 2\)

\(\max T =  - 2\,\,{\rm{khi}}\,\,t =  - 2;\,\,m = 1.\)

Cách khác: HS có thể áp dụng bất đẳng thức Cauchy.

Nhận xét: \({x_1},\,{x_2}\) là hai nghiệm trái dấu của phương trình nên \(\dfrac{{{x_1}}}{{{x_2}}} < 0.\)

Từ đó:

\(T = {\left( {\dfrac{{{x_1}}}{{{x_2}}}} \right)^3} + {\left( {\dfrac{{{x_2}}}{{{x_1}}}} \right)^3} \)\(\,=  - \left[ {{{\left( { - \dfrac{{{x_1}}}{{{x_2}}}} \right)}^3} + {{\left( { - \dfrac{{{x_2}}}{{{x_1}}}} \right)}^3}} \right] \)\(\,\le  - 2\sqrt {{{\left( { - \dfrac{{{x_1}}}{{{x_2}}}} \right)}^3}.{{\left( { - \dfrac{{{x_2}}}{{{x_1}}}} \right)}^3}}  =  - 2.\)

\(\max T =  - 2\,\,{\rm{khi}}\,\,t =  - 2;\,\,m = 1.\)

Bài VI:

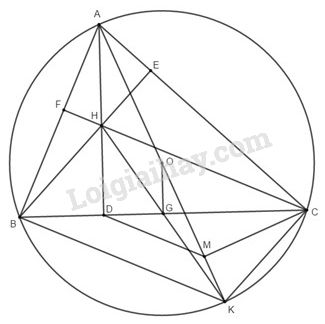
1) Xét tứ giác BFEC có góc BFC=BEC \(\widehat {BFC} = \widehat {BEC}\) vuông

Hai góc này cùng nhìn cạnh BC nên tứ giác này nội tiếp

2) Tam giác \(ABD\) đồng dạng với tam giác \(AKC\) và \(AB.AC = 2AD.R.\)

Đường tròn O có góc \(\widehat {ABC} = \widehat {AKC}\) nội tiếp chắn cung AC

Đường tròn O có AK là đường kính nên \(\widehat {ACK} = \widehat {ADB} = {90^o}\)

Vậy tam giác \(ABD\) đồng dạng với tam giác \(AKC\)

Từ đó suy ra \(\dfrac{{AB}}{{AK}} = \dfrac{{AD}}{{AC}} \)\(\,\Rightarrow AB.AC = AD.AK = AD.2R\)

3) Chứng minh: \(MD\) song song với \(BK.\)

Tứ giác ADMC nội tiếp do có \(\widehat {ADC} = \widehat {AMC} = {90^o}\)

Suy ra góc nội tiếp \(\widehat {CDM} = \widehat {CAM} = \widehat {CAK}\)

Đường tròn O có \(\widehat {CAK} = \widehat {CBK}\) suy ra \(\widehat {CBK} = \widehat {CDM}\) và BK//DM

4) Tìm vị trí của điểm \(A\) để diện tích tam giác \(AEH\) lớn nhất.

\(2{S_{\Delta AEH}} = AH.d(E,AH)\) mà tam giác AHK có OG là đường trung bình nên AH=2OG, O và G không đổi nên độ dài AH không đổi

\(\begin{array}{l}{S_{AEH}} = \dfrac{{AE.EH}}{2}\\\;\;\;\;\; \le \dfrac{{A{E^2} + E{H^2}}}{4} = \dfrac{{A{H^2}}}{4}\\\max {S_{AEH}} = \dfrac{{A{H^2}}}{4}.\\{S_{AEH}}\,\,{\rm{max }} \Leftrightarrow EA = EH\\ \Leftrightarrow \widehat E = {45^o} \Leftrightarrow \widehat {ACB} = {45^o}\end{array}\)

Bài V:

Có \(\dfrac{{{a^2}}}{{c({c^2} + {a^2})}} = \dfrac{{{a^2} + {c^2} - {c^2}}}{{c({c^2} + {a^2})}}\)\(\, = \dfrac{1}{c} - \dfrac{c}{{{c^2} + {a^2}}}\mathop  \ge \limits^{Cauchy} \dfrac{1}{c} - \dfrac{c}{{2\sqrt {{c^2}.\,\,{a^2}} }} \)\(\,= \dfrac{1}{c} - \dfrac{1}{{2a}}\)

\( \Rightarrow \dfrac{{{a^2}}}{{c({c^2} + {a^2})}} \ge \dfrac{1}{c} - \dfrac{1}{{2a}}\)

Và tương tự

\( \Rightarrow P \ge \left( {\dfrac{1}{c} - \dfrac{1}{{2a}}} \right) + \left( {\dfrac{1}{a} - \dfrac{1}{{2b}}} \right) \)\(\,+ \left( {\dfrac{1}{b} - \dfrac{1}{{2c}}} \right) = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}} \right) \)\(\,= \dfrac{{ab + bc + ca}}{{2abc}} = \dfrac{3}{2}\)

\( \Rightarrow MinP = \dfrac{3}{2}\), xảy ra \( \Leftrightarrow a = b = c = 1\).