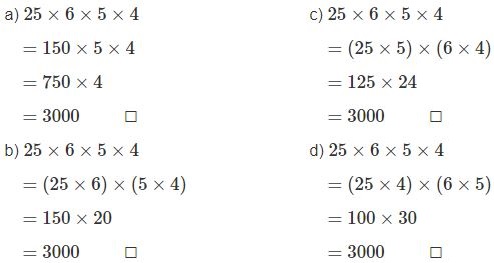Đề số 20 - Đề kiểm tra học kì 1 - Toán lớp 4

Đề bài

Câu 1. Đúng ghi Đ, sai ghi S :

Hình bên có :

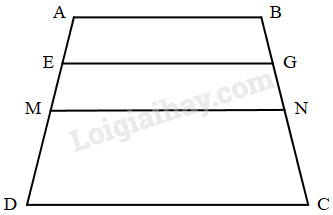
a) AD song song với BC.   ☐

b) AB song song với các cạnh EG, MN, DC.   ☐

c) Có 3 cặp cạnh song song với nhau.   ☐

d) Có 6 cặp cạnh song song với nhau.   ☐

Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng :

Tích của hai số là 12 480. Nếu một thừa số giảm đi 5 lần thì tích mới là :

A. 3120                                        B. 12485

C. 2500                                        D. 2496.

Câu 3. Đúng ghi Đ, sai ghi S :

Điền dấu \(( >, <, = )\) thích hợp vào chỗ chấm :

         \(3750 × 9 … 11250 × 3\)

a) \(3750 × 9  >  11250 × 3\)    ☐

b) \(3750 × 9 = 11250 ×3\)    ☐

c) \(3750 × 9 < 11250 × 3\)    ☐

Câu 4. Đánh dấu chéo (×) vào ô trống cạnh cách tính thích hợp nhất :

Câu 5. Tìm các số tự nhiên \(m\), biết \(48125 × m < 144370.\)

Câu 6. Khi nhân một số với 2468, Khuê đã viết nhầm chữ số 8 ở hàng đơn vị của số 2468 thành chữ số 3 nên tích giảm đi 35 đơn vị. Hãy tìm tích đúng.

Câu 7. Tính giá trị của biểu thức sau bằng cách hợp lí nhất :

\(2 × 4 × 5 × 6 × 15 × 25\)

Lời giải

Câu 1. 

Phương pháp:

Quan sát hình vẽ để tìm các cặp cạnh song song với nhau.

Cách giải:

Trong hình đã cho:

+) AD không song song với BC.

+) AB song song với các cạnh EG, MN, DC.

+) Có 6 cặp cạnh song song với nhau là:

    AB và EG ;                  AB và MN ;                AB và DC ;

    EG và MN ;                  EG và DC ;                MN và DC.

Vậy ta có kết quả như sau:

a) S,                           b) Đ,                         c) S,                          d) Đ

Câu 2. 

Phương pháp:

Tích của hai số là 12 480. Nếu một thừa số giảm đi 5 lần thì tích mới cũng giảm đi 5 lần.

Cách giải:

Tích của hai số là 12 480. Nếu một thừa số giảm đi 5 lần thì tích mới là:

                12 480 : 5 = 2496

Chọn D.

Câu 3.

Phương pháp:

Tính giá trị hai vế rồi so sánh kết quả với nhau. 

Cách giải:

Ta có:   3750 × 9 = 33 750  ;           11250 × 3 = 33 750.

Mà:      33 750 = 33 750

Vậy:     3750 × 9 … 11250 × 3.

Vậy ta có kết quả như sau:     a) S,                 b) Đ,                  c) S.

Câu 4. 

Phương pháp:

Ta thấy 25 × 4 = 100, do đó để tính thuận tiện nhất ta nhóm 25 và 4; 6 và 5 lại với nhau rồi thực hiện phép nhân như thông thương.

Cách giải:

Trong các cách tính đã cho cách tính thích hợp nhất là:

25 × 6 × 5 × 4 = (25 × 4) × (6 × 5) = 100 × 30 = 3000.

Chọn d.

Câu 5. 

Phương pháp:

Thay m = 0 ; 1 ; 2 ; 3 ; ... vào biểu thức 48 125 × m rồi tính giá trị biểu thức đó, sau đó so sánh kết quả với 144 370.

Cách giải:

Nếu m = 0 thì 48 125 × m = 48 125 × 0 = 0 < 144 370.

Nếu m = 1 thì 48 125 × 1 = 48 125 × 1 = 48 125 < 144 370.

Nếu m = 2 thì 48 125 × m = 48 125 × 2 = 96 250 < 144 370.

Nếu m = 3 thì 48 125 × 3 = 48 125 × 3 = 144 375 > 144 370.

Do đó, với m > 3 thì 48 125 × m > 144 370

Vậy để 48125 × m < 144370 thì m = 0 ; 1 ; 2.

Câu 6. 

Phương pháp:

Chữ số 8 ở hàng đơn vị của số 2468 viết nhầm thành chữ số 3. Số đó giảm số đơn vị là 8 – 3 = 5. 

Số thứ nhất giảm 5 đơn vị thì tích giảm đi số đơn vị bằng 5 lần số thứ hai, hay 5 lần số thứ hai là 35, từ đó tìm được số thứ hai.

Tích đúng = 2468 × số thứ hai vừa tìm được.

Cách giải:

Chữ số 8 ở hàng đơn vị của số 2468 viết nhầm thành chữ số 3. Số đó giảm số đơn vị là 8 – 3 = 5.

Số thứ nhất giảm 5 đơn vị thì tích giảm đi số đơn vị bằng 5 lần số thứ hai.

Do đó, 5 lần số thứ hai là 35.

Thừa số thứ hai (số nhân với 2468) là :

                  35 : 5 = 7

Tích đúng là :

                 2468 × 7 = 17276

                                     Đáp số : 17276.

Câu 7. 

Phương pháp:

Nhóm 2 và 5; 4 và 25; 6 và 15 lại thành 1 nhóm rồi thực hiện phép nhân như thông thường. 

Cách giải:

\(2 × 4 × 5 × 6 × 15 × 25\)

\(=(2 × 5) × (4 × 25) × (6 × 15)\)

\(=10 × 100 × 90\)

\(=1000 × 90 = 90 000.\)