Đề số 12 - Đề kiểm tra học kì 2 - Toán lớp 5

Đáp án và lời giải chi tiết Đề số 12 - Đề kiểm tra học kì 2 - Toán lớp 5

Đề bài

1. Đúng ghi Đ, sai ghi S vào ô trống :

A. 3km 4m = 3,04km
B. 3km 4m = 3,004km
C. 1750m = 1,75km
D. 1750m = 17,50km

2. Đúng ghi Đ, sai ghi S vào ô trống :

a. 1,07 tấn = 10,7 tạ
b. 1,07 tấn = 107 tạ

3. Đúng ghi Đ, sai ghi S vào ô trống :

a. 0,12ha + 75m² = 12 750m²
b. 0,12ha + 75m² = 1275m²
c. 0,5ha – 150m²= 4850m²
d. 0,5ha – 150m² = 350m²

4. Khoanh vào chữ đặt trước đáp số đúng.

12,5m²– 14,6dm² = … dm²

A. 1237,5dm²

B. 1235,4dm²

C. 110,4dm²

5. Đúng ghi Đ, sai ghi S vào ô trống :

a. 0,015 = 1,5%
b. 0,015 = 1,05%

6. Đúng ghi Đ, sai ghi S vào ô trống :

a) \(4{m^3}\;15d{m^3} = 4,15{m^3}\)
b) \(4{m^3}\;15d{m^3} = 4,015{m^3}\)
c) \(2{m^3}\;2d{m^3} = 2,002{m^3}\)
d) \(2{m^3}\;2d{m^3} = 2,2{m^3}\)

7. Đúng ghi Đ, sai ghi S vào ô trống :

Từ một bao đường, người ta lấy ra 27kg, chiếm 45% lượng đường trong bao. Hỏi lúc đầu bao đường đó có bao nhiêu ki-lô-gam đường ?

A. 50kg
B. 60kg
C. 70kg

8. Đúng ghi Đ, sai ghi S vào ô trống :

0,45 giờ + 15 phút = … phút. Số điền vào chỗ chấm là :

A. 42
B. 60
C. 72

9. Đúng ghi Đ, sai ghi S vào ô trống :

Một tam giác có đáy là \(\dfrac{4}{5}m.\) Chiều cao bằng \(\dfrac{1}{2}\) đáy. Tính diện tích hình tam giác đó.

A. \(\dfrac{8}{{25}}{m^2}\)
B. \(\dfrac{2}{5}{m^2}\)
C. \(\dfrac{4}{{25}}{m^2}\)

10. Kho thứ nhất có nhiều hơn kho thứ hai 27,6 tạ gạo. Sau khi lấy đi ở mỗi kho 18 tạ gạo thì số gạo còn lại trong kho thứ hai bằng \(\dfrac{4}{7}\) số gạo còn lại trong kho thứ nhất. Hỏi lúc đầu trong mỗi kho có bao nhiêu tạ gạo ?

11. Hình vẽ cho biết : ABCD là hìnhchữ nhật, có AB = 24cm ;AD = 18cm ; MB = 8cm ; BE = EC.

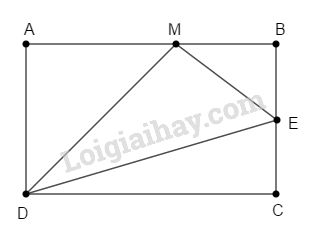
a. Tính diện tích hình thang MBCD.

b. Tính diện tích tam giác MED.

Lời giải chi tiết

Phương pháp:

Áp dụng cách đổi: 1km = 1000m, hay 1m = \(\dfrac{1}{1000}\)km.

Cách giải:

3km 4m = \(3\dfrac{4}{1000}\)km = 3,004km;

1750m = \(\dfrac{1750}{1000}\)km = 1,750km = 1,75km.

Ta có bảng kết quả như sau:

A. 3km 4m = 3,04km	S
B. 3km 4m = 3,004km	Đ
C. 1750m = 1,75km	Đ
D. 1750m = 17,50km	S

Phương pháp:

1 tấn = 10 tạ. Muốn đổi một số từ đơn vị tấn sang đơn vị tạ ta chỉ cần lấy 10 tạ nhân với số đó

Cách giải:

Ta có 1 tấn = 10 tạ nên 1,07 tấn = 10 tạ ⨯ 1,07 = 10,7 tạ.

Ta có bảng kết quả như sau:

a. 1,07 tấn = 10,7 tạ	Đ
b. 1,07 tấn = 107 tạ	S

Phương pháp:

Đổi các số đo về cùng đơn vị đo rồi thực hiện phép cộng, phép trừ các số đo tương tự như đối với các số tự nhiên.

Lưu ý rằng: 1ha = 10 000m².

Cách giải:

a. 0,12ha + 75m² = 1200m²+ 75m²= 1275m².

b. 0,5ha – 150m²= 5000m² – 150m² = 4850m²

Ta có bảng kết quả như sau:

a. 0,12ha + 75m² = 12 750m²	S
b. 0,12ha + 75m² = 1275m²	Đ
c. 0,5ha – 150m²= 4850m²	Đ
d. 0,5ha – 150m² = 350m²	S

Phương pháp:

Đổi các số đo về cùng đơn vị đo rồi thực hiện phép trừ các số đo tương tự như đối với các số tự nhiên.

Lưu ý rằng: 1m²= 100dm².

Cách giải

12,5m² – 14,6dm²= 1250dm² – 14,6dm² = 1235,4dm²

Chọn B.

Phương pháp:

Áp dụng cách viết gọn: \(\dfrac{1}{100}\)= 1%, hay 0,01 = 1%.

Cách giải:

a. 0,015 = 1,5%	Đ
b. 0,015 = 1,05%	S

Phương pháp:

Dựa vào cách đổi: 1m³= 1000dm³

Cách giải:

4m³ 15dm³= \(4\dfrac{15}{1000}\)m³ = 4,015m³

2m³ 2dm³= \(2\dfrac{2}{1000}\)m³ = 2,002m³

a) \(4{m^3}\;15d{m^3} = 4,15{m^3}\)	S
b) \(4{m^3}\;15d{m^3} = 4,015{m^3}\)	Đ
c) \(2{m^3}\;2d{m^3} = 2,002{m^3}\)	Đ
d) \(2{m^3}\;2d{m^3} = 2,2{m^3}\)	S

Phương pháp:

Theo đề bài ta có 45% lượng đường trong bao là 27kg. Muốn tìm số đường trong bao ta lấy 27 chia cho 45 rồi nhân với 100, sau đó ghi thêm đơn vị đo vào kết quả.

Cách giải:

Lúc đầu bao đường đó có số ki-lô-gam đường là:

27 : 45 ⨯ 100 = 60 (kg)

A. 50kg	S
B. 60kg	Đ
C. 70kg	S

Phương pháp:

- Đổi các số đo về cùng đơn vị đo rồi thực hiện phép cộng các số đo tương tự như đối với các số tự nhiên.

- 1 giờ = 60 phút. Muốn đổi một số từ đơn vị giờ sang đơn vị phút ta chỉ cần lấy 60 phút nhân với số đó.

Cách giải:

Ta có: 0,45 giờ = 60 phút ⨯ 0,45 = 27 phút)

Do đó: 0,45 giờ + 15 phút = 27 phút + 15 phút = 42 phút.

Ta có bảng kết quả như sau:

A. 42	Đ
B. 60	S
C. 72	S

Phương pháp:

- Tính chiều cao ta lấy độ dài đáy nhân với \(\dfrac{1}{2}\).

- Muốn tính diện tích tam giác ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2 (cùng đơn vị đo).

Cách giải:

Chiều cao của tam giác đó là:

\(\dfrac{4}{5} \times \dfrac{1}{2}= \dfrac{2}{5}\;(m)\)

Diện tích tam giác đó là:

\(\dfrac{4}{5} \times \dfrac{2}{5} : 2= \dfrac{4}{25}\;(m^2)\)

Ta có bảng kết quả như sau:

A. \(\dfrac{8}{{25}}{m^2}\)	S
B. \(\dfrac{2}{5}{m^2}\)	S
C. \(\dfrac{4}{{25}}{m^2}\)	Đ

10.

Phương pháp:

- Khi lấy đi ở mỗi kho 18 tạ gạo thì hiệu số gạo hai kho không thay đổi, hay số gạo còn lại ở kho thứ nhất vẫn hơn số gạo còn lại ở kho thứ hai là 27,6 tạ.

- Ta tìm số gạo còn lại của mỗi kho theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó.

- Tìm số gạo lúc đầu đầu của mỗi kho ta lấy số gạo còn lại cộng với số gạo đã lấy ra.

Cách giải:

Khi lấy đi ở mỗi kho 18 tạ gạo thì hiệu số gạo hai kho không thay đổi, hay số gạo còn lại ở kho thứ nhất vẫn hơn số gạo còn lại ở kho thứ hai là 27,6 tạ.

Coi số gạo còn lại ở kho thứ hai gồm 4 phần bằng nhau thì số gạo còn lại ở kho thứ nhất gồm 7 phần như thế.

Hiệu số phần bằng nhau là:

7 - 4 = 3 (phần)

Số gạo còn lại ở kho thứ nhất là:

27,6 : 3 ⨯ 7 = 64,4 (tạ)

Số gạo lúc đầu ở kho thứ nhất là:

64,4 + 18 = 82,4 (tạ)

Số gạo lúc đầu ở kho thứ hai là:

82,4 – 27,6 = 54,8 (tạ)

Đáp số: Kho thứ nhất: 82,4 tạ;

Kho thứ hai: 54,8 tạ.

11.