Đề số 12 - Đề kiểm tra học kì 1 - Toán 6

Đề bài

Bài 1 (2 điểm) Chọn chữ cái đứng trước câu trả lời đúng

 1 . Cho tập hợp \(A = {\rm{\{ a}} \in {\rm{N | 5}} \le {\rm{x  < 8\} }}\) có số phần tử là

A. 2                             B. 3

C. 4                             D. 5

2 . Nếu \(a \vdots 6\) và \(b \vdots 9\) thì \(a + b\)   chia hết cho

A. 2                             B. 3

C. 6                             D. 9

3 . Cho \(a = {2^3}{.3.5^2}\) và \(b = {2^2}{.3^2}.5\) thì BCNN(a; b) bằng

A. \({2^2}.3.5\)                B. \({2^3}{.3.5^2}\)

C. \(2.3.5\)                   D.\({2^3}{.3^2}{.5^2}\)

4 . Số nào sau đây là số nguyên tố?

A. 51                           B. 71

C. 81                           D. 91

5 . Kết quả của phép tính \({2^{30}}:{2^{10}}\) là:

A. \({2^{20}}\)                                    B. \({2^3}\)

C. \({2^{10}}\)                                    D. \({1^{20}}\)

6 . Kết quả của phép tính \(( - 11) + ( - 9)\) là:

A. 20                           B. –2

C. –20                         D. 2

7 . Chọn câu đúng trong các phát biểu sau:

A. Hai tia Ox, Oy chung gốc thì đối nhau.                

B. Hai tia Ox, Oy tạo thành đường thẳng xy thì đối nhau.               

C. Nếu A, B, C thẳng hàng thì AB + BC = AC.                  

D. Trong 3 điểm có 1 và chỉ 1 điểm nằm giữa hai điểm còn lại.

8 . Trên tia Om lấy điểm A sao cho OA = 6cm. Gọi I là điểm nằm giữa O và A sao cho \(OI = \dfrac{1}{2}OA\). Kết luận nào sau đây không đúng?

A. OI + IA = OA

B. IA = 3cm               

C. I là trung điểm của OA

D. OI > IA

Bài 2  (1,5 điểm) Thực hiện phép tính:

a) \(23.134 - 34.23\)

b)  \(\left( { - 297} \right) + 630 + 297 + \left( { - 330} \right)\)

c) \({10^2} - 60:({5^6}:{5^4} - 3.5)\)

Bài 3 (2,0 điểm) Tìm số nguyên x biết:

a) \(75:x = \left( { - 5} \right) + 20\)

b) \({5^{x + 5}} - {2017^0} = {2^3}.3\)

Bài 4  (1,5 điểm): Cô giáo muốn chia 48 bút bi, 36 quyển vở và 24 thước kẻ thành các phần thưởng sao cho mỗi phần thưởng có số bút, số vở  và số thước kẻ như nhau. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng? Khi đó, mỗi phần thưởng có bao nhiêu bút bi, bao nhiêu vở , bao nhiêu thước kẻ?

Bài 5 (2 điểm) Trên tia Ox lấy hai điểm M, N sao cho OM = 2cm, ON = 5cm.

a) Trong ba điểm O, M, N, điểm nào nằm giữa hai điểm còn lại? Vì sao?

b) Tính độ dài MN.

c) Vẽ tia Ox’ là tia đối của tia Ox. Lấy điểm D trên tia Ox’ sao cho OD = 1cm. Điểm M có là trung điểm của đoạn thẳng ND không? Vì sao?

Bài 6 (0,5 điểm) So sánh hai lũy thừa: \({199^{20}}\) và \({2017^{15}}\).

Lời giải chi tiết

Bài 1.

Bài 2

\(\begin{array}{l}a)\;\;23.134 - 34.23\\ = 23.\left( {134 - 34} \right)\\ = 23.100\\ = 2300.\end{array}\)     

\(\begin{array}{l}b)\;\;\left( { - 297} \right) + 630 + 297 + \left( { - 330} \right)\\ = \left( { - 297 + 297} \right) + \left[ {630 + \left( { - 330} \right)} \right]\\ = 0 + 630 - 330\\ = 300.\end{array}\)

\(\begin{array}{l}c)\;\;{10^2} - 60:({5^6}:{5^4} - 3.5)\\ = {10^2} - 60:({5^2} - 15)\\ = 100 - 60:(25 - 15)\\ = 100 - 60:10\\ = 100 - 6\\ = 94\end{array}\)                                            

Bài 3

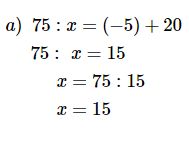
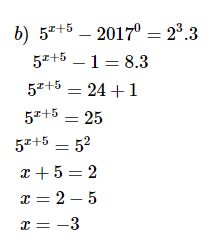
Bài 4

Gọi số phần thưởng được chia là \(x\,\,(x > 0)\).

Theo đề bài ta phải có \(48\,\, \vdots \,\,x\,\,;\,\,36\,\, \vdots \,\,x\,;\,\,\,24\,\, \vdots \,\,x\,\,\)và \(x\) là lớn nhất. Do đó \(x\) là \(UCLN\left( {48;\;36;\;24} \right).\)

Ta có: \(48 = {2^4}.3\,\,\,\,;\,\,\,\,\,\,\,\,\,\,36 = {2^2}{.3^2}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,24 = {2^3}.3\).

\(UCLN\left( {48;\;36;\;24} \right) = {2^2}.3\,\, = \,\,12\). Do đó \(x = 12\).

Vậy ta chia được nhiều nhất là 12 phần thưởng.

Khi đó mỗi phần thưởng có số cái bút là:       48 : 12 = 4 (cái bút)

Mỗi phần thưởng có số quyển vở  là:             36 : 12 = 3 (quyển vở)

Mỗi phần thưởng có số thước kẻ là:               24 : 12 = 2 (thước kẻ).

Bài 5

a) Trên tia Ox ta có \(OM < ON\;\left( {do\;\;2cm < \;\;5cm} \right)\)  nên điểm M nằm giữa hai điểm O và N.

b) Vì điểm M nằm giữa hai điểm O và N (chứng minh câu a)) nên ta có \(OM + MN = ON\)

\( \Rightarrow MN = ON - OM = 5 - 2 = 3\,cm\)

c) Ta có điểm M thuộc tia Ox, điểm D thuộc tia Ox’ và tia Ox’ là tia đối của tia Ox nên O là điểm nằm giữa hai điểm D và M.

\( \Rightarrow DO + OM = DM\)

\(\Rightarrow DM = DO + OM = 1 + 2 = 3\,\,(cm)\)

 Ta có điểm N thuộc tia Ox, điểm D thuộc tia Ox’ và tia Ox’ là tia đối của tia Ox nên O là điểm nằm giữa hai điểm D và N.

Lại có DM = MN = 3cm (cmt).

Suy ra điểm M là trung điểm của đoạn thẳng ND.

Bài 6

Ta có: \({199^{20}} < {200^{20}}\,\,\,;\,\,\,\,{2000^{15}} < \,\,{2017^{15}}\,\,\,\,\,\,\,\,\,\,(1)\)

So sánh \({200^{20}}\) và \({2000^{15}}\)ta có :

\(\begin{array}{l}{200^{20}}\, = {200^{15}}\,.\,\,{200^5}\,\,;\\{2000^{15}} = {(200.10)^{15}} = {200^{15}}{.10^{15}} = {200^{15}}{.10^{3.5}} \\\;\;\;\;\;\;\;\;\;\;\;= {200^{15}}.{\left( {{{10}^3}} \right)^5} = {200^{15}}{.1000^5}\end{array}\)

Mà \({200^5} < {1000^5}\) nên \({200^{15}}\,.\,\,{200^5}\,\, < \,\,\,{200^{15}}\,.\,\,{1000^5}\,\,\).

Do đó \({200^{20}}\, < \,\,{2000^{15}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\)

Từ (1) và (2) suy ra \({199^{20}} < \,\,\,\,{2017^{15}}\).  

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 6 tại TimDapAn.com