Đề kiểm tra học kì 1 Toán 7 - Đề số 8 - Cánh diều
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Kết quả của phép tính: \(\left( {1 + 1\dfrac{1}{2}} \right):\dfrac{{ - 7}}{4}\) là:
A. \(\dfrac{{20}}{{ - 7}}\) B. \(\dfrac{{10}}{{ - 7}}\) C. \(\dfrac{{ - 5}}{{ - 14}}\) D. \(\dfrac{5}{{ - 7}}\)
Câu 2: Tìm \(x\), biết: \(x + \left( {\dfrac{1}{4}x - 2,5} \right) = \dfrac{{ - 11}}{{20}}\)
A. \(x = \dfrac{{39}}{{25}}\) B. \(x = \dfrac{{19}}{{20}}\) C. \(x = \dfrac{{17}}{{20}}\) D. \(x = \dfrac{{11}}{{25}}\)
Câu 3: Kết quả của biểu thức: \(2,8 + 3.\left| { - \dfrac{{13}}{3}} \right| + 0,2.\left| 6 \right| + 5.\left| {10} \right|\) là:
A. \(41\) B. \(53\) C. \(47\) D. \(67\)
Câu 4: Thứ tự tăng dần của các số: \(\sqrt {\dfrac{1}{{16}}} \,;\,4\dfrac{1}{7}\,;\,1,\left( 3 \right)\,;\,\sqrt {81} \,;\, - \sqrt {25} \,;\, - 12,1\) là:
A. \(\sqrt {81} \,\,;\,\,4\dfrac{1}{7}\,\,;\,\,1,\left( 3 \right)\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\, - 5\,\,;\,\, - 12,1\) B. \(\sqrt {81} \,\,;\,\,4\dfrac{1}{7}\,\,;\,\,1,\left( 3 \right)\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\, - 12,1\,\,;\,\, - 5\)
C. \( - 12,1\,\,;\,\, - 5\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\,1,\left( 3 \right)\,\,;\,\,4\dfrac{1}{7}\,\,;\,\,\sqrt {81} \) D. \( - 5\,\,;\,\, - 12,1\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\,1,\left( 3 \right)\,\,;\,\,4\dfrac{1}{7}\,\,;\,\,\sqrt {81} \)
Câu 5: Một chiếc bánh kem có dạng hình hộp chữ nhật với chiều dài 30cm, chiều rộng 20cm và chiều cao 15cm. Người ta cắt đi ba miếng bánh có dạng hình lập phương cạnh 5cm. Tính thể tích phần còn lại của chiếc bánh kem.
A. \(8875c{m^3}\) B. \(8875c{m^2}\) C. \(8625c{m^3}\) D. \(8625c{m^2}\)
Câu 6: Một quyển lịch để bàn gồm các tờ lịch được đặt trên một giá đỡ bằng bìa có dạng hình lăng trụ đứng tam giác. Tính diện tích bìa dùng để làm giá đỡ của quyển lịch.
A. \(1175\,c{m^2}\) B. \(1000\,c{m^2}\) C. \(1200\,c{m^2}\) D. \(1250\,c{m^2}\)
Câu 7: Cho hai góc kề bù \(AOB\) và \(BOC\). Tia \(OM\) nằm giữa hai tia \(OB\) và \(OC\). Tia \(ON\) là tia đối của tia \(OM\). Khi đó cặp góc đối đỉnh là cặp góc nào trong các góc sau đây?
A. \(\angle BOM\) và \(\angle CON\) B. \(\angle AOB\) và \(\angle AON\) C. \(\angle AOM\) và \(\angle CON\) D. \(\angle COM\) và \(\angle CON\)
Câu 8: Cho hình vẽ bên dưới. Biết \(AB//CD\)\(,\angle A = {70^0},\angle B = {60^0}.\) Tính số đo của góc \(ACB?\)
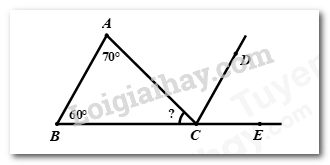
A. \(\angle ACB = {70^0}\) B. \(\angle ACB = {60^0}\) C. \(\angle ACB = {130^0}\) D. \(\angle ACB = {50^0}\)
Câu 9: Một ô tô đi quãng đường 135 km với vận tốc v (km/h) và thời gian t (h). Chọn câu đúng về mối quan hệ của v và t.
A. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ \(\dfrac{1}{{135}}\)
B. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 135
C. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ \(\dfrac{1}{{135}}\)
D. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 135.
Câu 10: Chọn câu đúng. Với điều kiện các phân thức có nghĩa thì:
A. \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x + y}}{{a + b}}\) B. \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x.y}}{{a.b}}\)
C. \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x.y}}{{a + b}}\) D. \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x - y}}{{a + b}}\)
Phần II. Tự luận (7 điểm):
Bài 1: (1,5 điểm)
Thực hiện phép tính:
a) \(\left( { - \dfrac{1}{5} + \dfrac{3}{7}} \right):\dfrac{5}{4} + \left( {\dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right):\dfrac{5}{4}\)
b) \(3.\sqrt {\dfrac{1}{9}} + 1,5.\sqrt {225} \)
c) \(\left( { - 1,5} \right) + 2.\left| {2\dfrac{1}{2}} \right| - 6.\left| {\dfrac{{ - 16}}{3}} \right| + 5.\left| { - 0,3} \right|\)
Bài 2: (1,5 điểm)
Tìm \(x\), biết:
a) \(x:\left( { - \dfrac{3}{5}} \right) = 1\dfrac{1}{4}\)
b) \({\left( {0,9} \right)^9}:x = - {\left( {0,9} \right)^7}\)
c) \(\left| {x - 12} \right| = \sqrt 5 - \sqrt 7 \)
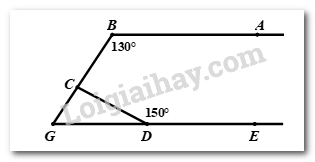
Bài 3: (1 điểm) Cho hình vẽ bên dưới, biết \(AB//DE\). Tìm số đo góc \(\angle BCD\)?
Bài 4: (1 điểm) Một bể cá dạng hình hộp chữ nhật làm bằng kính (không có nắp) có chiều dài \(80cm\), chiều rộng \(50cm\), chiều cao \(45cm\). Mực nước ban đầu trong bể cao \(35cm\).
a) Tính diện tích kính dùng để làm bể cá đó.
b) Người ta cho vào bể một hòn đá trang trí chìm hẳn trong nước thì mực nước của bể dâng lên thành \(37,5cm\). Tính thể tích hòn đá.
Bài 5: (1,5 điểm) Ba công nhân có năng suất lao động tương ứng tỉ lệ với 3; 5; 7 . Tính tổng số tiền ba người được thưởng nếu biết tổng số tiền thưởng của người thứ nhất và người thứ hai là 5,6 triệu đồng.
Bài 6: (0,5 điểm)
Cho ba số \(x,y,z\) thỏa mãn: \(\dfrac{x}{{2018}} = \dfrac{y}{{2019}} = \dfrac{z}{{2020}}\). Chứng minh rằng:
\({\left( {x - z} \right)^3} = 8{\left( {x - y} \right)^2}\left( {y - z} \right)\)
Lời giải
Phần I: Trắc nghiệm:
|
1.B |
2.A |
3.D |
4.C |
5.C |
6.A |
7.C |
8.D |
9.B |
10.A |
Câu 1:
Phương pháp:
Đổi hỗn số về phân số
Thực hiện phép cộng, phép chia số hữu tỉ.
Cách giải:
\(\left( {1 + 1\dfrac{1}{2}} \right):\dfrac{{ - 7}}{4} = \left( {1 + \dfrac{3}{2}} \right).\dfrac{4}{{ - 7}} = \left( {\dfrac{2}{2} + \dfrac{3}{2}} \right).\dfrac{4}{{ - 7}} = \dfrac{5}{2}.\dfrac{4}{{ - 7}} = \dfrac{{10}}{{ - 7}}\)
Chọn B.
Câu 2:
Phương pháp:
Vận dụng quy tắc chuyển vế tìm \(x\).
Cách giải:
\(x + \left( {\dfrac{1}{4}x - 2,5} \right) = \dfrac{{ - 11}}{{20}}\)
\(\begin{array}{l}x + \dfrac{1}{4}x - \dfrac{{50}}{{20}} = \dfrac{{ - 11}}{{20}}\\\left( {1 + \dfrac{1}{4}} \right).x = \dfrac{{ - 11}}{{20}} + \dfrac{{50}}{{20}}\\\left( {\dfrac{4}{4} + \dfrac{1}{4}} \right).x = \dfrac{{39}}{{20}}\\\dfrac{5}{4}.x = \dfrac{{39}}{{20}}\\x = \dfrac{{39}}{{20}}:\dfrac{5}{4}\\x = \dfrac{{39}}{{20}}.\dfrac{4}{5}\\x = \dfrac{{39}}{{25}}\end{array}\)
Vậy \(x = \dfrac{{39}}{{25}}\)
Chọn A.
Câu 3:
Phương pháp:
Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
\(2,8 + 3.\left| { - \dfrac{{13}}{3}} \right| + 0,2.\left| 6 \right| + 5.\left| {10} \right|\)
\(\begin{array}{l} = 2,8 + 3.\left[ { - \left( { - \dfrac{{13}}{3}} \right)} \right] + 0,2.6 + 5.10\\ = 2,8 + 3.\dfrac{{13}}{3} + 1,2 + 50\\ = 2,8 + 13 + 1,2 + 50\\ = 67\end{array}\)
Chọn D.
Câu 4:
Phương pháp:
Tính các căn bậc hai của một số, đổi từ số thập phân vô hạn tuần hoàn sang phân số.
So sánh các phân số có cùng mẫu dương.
Từ đó sắp xếp được các số theo thứ tự tăng dần.
Cách giải:
Ta có:
\(\begin{array}{l}\sqrt {\dfrac{1}{{16}}} = \dfrac{1}{4} = \dfrac{{21}}{{84}};\\4\dfrac{1}{7} = \dfrac{{29}}{7} = \dfrac{{348}}{{84}};\\1,\left( 3 \right) = 1 + 3.0,1 = 1 + 3.\dfrac{1}{9} = 1 + \dfrac{1}{3} = \dfrac{3}{3} + \dfrac{1}{3} = \dfrac{4}{3} = \dfrac{{112}}{{84}};\\\sqrt {81} = 9 = \dfrac{{756}}{{84}};\\ - \sqrt {25} = - 5;\,\\ - 12,1.\end{array}\)
Vì \(5 < 12,1\) nên \( - 5 > - 12,1\)
Vì \(21 < 112 < 348 < 756\) nên \(\dfrac{{21}}{{84}} < \dfrac{{112}}{{84}} < \dfrac{{348}}{{84}} < \dfrac{{756}}{{84}}\) suy ra \(\sqrt {\dfrac{1}{{16}}} < 1,\left( 3 \right) < 4\dfrac{1}{7} < \sqrt {81} \)
Thứ tự tăng dần của các số được sắp xếp là: \( - 12,1\,\,;\,\, - 5\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\,1,\left( 3 \right)\,\,;\,\,4\dfrac{1}{7}\,\,;\,\,\sqrt {81} \).
Chọn C.
Câu 5:
Phương pháp:
Thể tích của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c:V = abc\)
Thể tích của hình lập phương có một cạnh là \(a:V = {a^3}\)
Cách giải:
Thể tích chiếc bánh kem dạng hình hộp chữ nhật ban đầu là: \(30.20.15 = 9000\,\left( {c{m^3}} \right)\)
Thể tích của một miếng kem có dạng hình lập phương là: \({5^3} = 125\,\left( {c{m^3}} \right)\)
Khi đó, thể tích của ba miếng bánh bị cắt đi là: \(3.125 = 375\,\left( {c{m^3}} \right)\)
Thể tích phần còn lại của chiếc bánh kem là: \(9000 - 375 = 8625\,\left( {c{m^3}} \right)\)
Chọn C.
Câu 6:
Phương pháp:
Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: \({S_{xq}} = C.h\)
Trong đó: \({S_{xq}}:\) diện tích xung quanh của hình lăng trụ
\(C:\) chu vi một đáy của hình lăng trụ
\(h:\) chiều cao lăng trụ
Cách giải:
Diện tích bìa dùng để làm giá đỡ của quyển lịch là diện tích xung quanh của hình lăng trụ đứng tam giác:
\({S_{xq}} = C.h = \left( {20 + 20 + 7} \right).25 = 47.25 = 1175\,\left( {c{m^2}} \right)\)
Chọn A.
Câu 7:
Phương pháp:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Cách giải:
\(\angle AOB\) và \(\angle BOC\) là hai góc kề bù nên \(OA\) và \(OC\) là hai tia đối nhau
Lại có: \(ON\) là tia đối của tia \(OM\)
Do đó, \(\angle AOM\) và \(\angle CON\) là hai góc đối đỉnh.
Chọn C.
Câu 8:
Phương pháp:
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song với nhau thì hai góc ở vị trí so le trong bằng nhau; hai góc ở vị trí đồng vị bằng nhau.
Hai góc kề bù có tổng số đo góc bằng \({180^0}\).
Cách giải:
Vì \(AB//CD\) nên ta có:
\(\angle BAC = \angle ACD = {70^0}\) (hai góc so le trong)
\(\angle ABC = \angle DCE = {60^0}\) (hai góc đồng vị)
Ta có: \(\angle ACD\) và \(\angle DCE\) là hai góc kề nhau nên \(\angle ACE = \angle ACD + \angle DCE = {70^0} + {60^0} = {130^0}\)
Ta có: \(\angle ACB\) và \(\angle ACE\) là hai góc kề bù nên \(\angle ACB + \angle ACE = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle ACB + {130^0} = {180^0}\\ \Rightarrow \angle ACB = {180^0} - {130^0} = {50^0}\end{array}\)
Vậy \(\angle ACB = {50^0}\)
Chọn D.
Câu 9:
Phương pháp:
+ Thời gian và vận tốc của một phương tiện đi trên một quãng đường là hai đại lượng tỉ lệ nghịch.
+ Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = \dfrac{a}{x}\) hay \(x.y = a\) (a là hằng số khác 0) thì y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Cách giải:
Theo bài ra ta có: \(v.t = 135 \Rightarrow v = \dfrac{{135}}{t}\,\) và \(t = \dfrac{{135}}{v}\)
Nên v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 135
Chọn B
Câu 10:
Phương pháp:
Sử dụng tính chất dãy tỉ số bằng nhau.
Cách giải:
Ta có \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x + y}}{{a + b}} = \dfrac{{x - y}}{{a - b}}\)
Chọn A.
Phần II. Tự luận:
Bài 1:
Phương pháp:
a) Vận dụng tính chất kết hợp của phép nhân và phép cộng tính hợp lí.
b) Tính lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\)
Thực hiện các phép toán với các số hữu tỉ.
c) Tính căn bậc hai.
Thực hiện các phép toán với các số hữu tỉ.
d) Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Thực hiện các phép toán với các số hữu tỉ.
Cách giải:
a) \(\left( { - \dfrac{1}{5} + \dfrac{3}{7}} \right):\dfrac{5}{4} + \left( {\dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right):\dfrac{5}{4}\)
\(\begin{array}{l} = \left( { - \dfrac{1}{5} + \dfrac{3}{7}} \right).\dfrac{4}{5} + \left( {\dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right).\dfrac{4}{5}\\ = \left( { - \dfrac{1}{5} + \dfrac{3}{7} + \dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right).\dfrac{4}{5}\\ = \left[ {\left( { - \dfrac{1}{5} + \dfrac{{ - 4}}{5}} \right) + \left( {\dfrac{3}{7} + \dfrac{4}{7}} \right)} \right].\dfrac{4}{5}\\ = \left( {\dfrac{{ - 5}}{5} + \dfrac{7}{7}} \right).\dfrac{4}{5}\\ = \left( { - 1 + 1} \right).\dfrac{4}{5}\\ = 0.\dfrac{4}{5} = 0\end{array}\)
b) \(3.\sqrt {\dfrac{1}{9}} + 1,5.\sqrt {225} \)
\(\begin{array}{l} = 3.\dfrac{1}{3} + \dfrac{3}{2}.15\\ = 1 + \dfrac{{45}}{2}\\ = \dfrac{2}{2} + \dfrac{{45}}{2}\\ = \dfrac{{47}}{2}\end{array}\)
c) \(\left( { - 1,5} \right) + 2.\left| {2\dfrac{1}{2}} \right| - 6.\left| {\dfrac{{ - 16}}{3}} \right| + 5.\left| { - 0,3} \right|\)
\(\begin{array}{l} = - 1,5 + 2.2\dfrac{1}{2} - 6.\left[ { - \left( {\dfrac{{ - 16}}{3}} \right)} \right] + 5.\left[ { - \left( { - 0,3} \right)} \right]\\ = - 1,5 + 2.\dfrac{5}{2} - 6.\dfrac{{16}}{3} + 5.0,3\\ = - 1,5 + 5 - 32 + 1,5\\ = \left( { - 1,5 + 1,5} \right) + \left( {5 - 32} \right)\\ = 0 + \left( { - 27} \right)\\ = - 27\end{array}\)
Bài 2:
Phương pháp:
a) Thực hiện phép nhân hai số hữu tỉ, tìm \(x\).
b) Thực hiện phép chia hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\)
c) Tính căn bậc hai
Vận dụng quy tắc chuyển vế tìm \(x\)
d) \(\left| x \right| = a\)
Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\)
Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
a) \(x:\left( { - \dfrac{3}{5}} \right) = 1\dfrac{1}{4}\)
\(\begin{array}{l}x:\left( { - \dfrac{3}{5}} \right) = \dfrac{5}{4}\\x = \dfrac{5}{4}.\left( { - \dfrac{3}{5}} \right)\\x = \dfrac{{ - 3}}{4}\end{array}\)
Vậy \(x = \dfrac{{ - 3}}{4}\)
b) \({\left( {0,9} \right)^9}:x = - {\left( {0,9} \right)^7}\)
\(\begin{array}{l}x = {\left( {0,9} \right)^9}:\left[ { - {{\left( {0,9} \right)}^7}} \right]\\x = - \left[ {{{\left( {0,9} \right)}^9}:{{\left( {0,9} \right)}^7}} \right]\\x = - {\left( {0,9} \right)^{9 - 7}}\\x = - {\left( {0,9} \right)^2}\\x = - 0,81\end{array}\)
Vậy \(x = - 0,81\)
c) \(\left| {x - 12} \right| = \sqrt 5 - \sqrt 7 \)
Vì \(5 < 7\) nên \(\sqrt 5 < \sqrt 7 \) do đó, \(\sqrt 5 - \sqrt 7 < 0\)
Vì \(\left| {x - 12} \right| \ge 0\) với mọi số thực \(x\) mà \(\sqrt 5 - \sqrt 7 < 0\) nên không có giá trị nào của \(x\) thỏa mãn \(\left| {x - 12} \right| = \sqrt 5 - \sqrt 7 \).
Vậy \(x \in \emptyset \)
Bài 3:
Phương pháp:
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song có hai góc trong cùng phía bù nhau.
Cách giải:
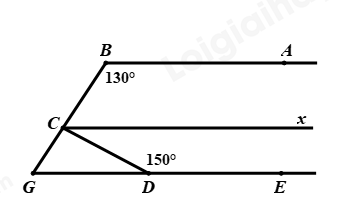
Kẻ \(Cx//AB\)
Vì \(Cx//AB\) (cách kẻ) nên \(\angle ABC + \angle BCx = {180^0}\) (hai góc trong cùng phía)
Suy ra \(\angle BCx = {180^0} - \angle ABC = {180^0} - {130^0} = {50^0}\)
Vì \(AB//DE\) nên \(\angle ABC + \angle BGE = {180^0}\) (hai góc trong cùng phía).
Suy ra \(\angle BGE = \angle BCx\) (cùng bù với \(\angle ABC\)).
Mà \(\angle BGE,\angle BCx\) ở vị trí đồng vị nên \(Cx//GE.\)
Suy ra \(\angle DCx + \angle CDE = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \angle DCx = {180^0} - \angle CDE = {180^0} - {150^0} = {30^0}\)
Vì \(\angle BCx\) và \(\angle DCx\) là hai góc kề nhau nên \(\angle BCD = \angle BCx + \angle DCx = {50^0} + {30^0} = {80^0}\)
Bài 4:
Phương pháp:
a) Diện tích xung quanh của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c\): \({S_{xq}} = 2.\left( {a + b} \right).c\)
b) Thể tích của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c:V = abc\)
Cách giải:
a) Diện tích kính dùng làm bể cá đó là tổng diện tích của bốn mặt bên và diện tích của mặt đáy bể.
Vậy diện tích kính dùng để làm bể cá là: \(2.\left( {80 + 50} \right).45 + 80.50 = 15\,700\left( {c{m^2}} \right)\)
b) Thể tích của hòn đá là hiệu thể tích sau cho hòn đá vào bể và thể tích ban đầu của bể cá.
Thể tích ban đầu của bể cá là: \(80.50.35 = 140\,000\left( {c{m^3}} \right)\)
Thể tích của bể cá sau khi cho vào hòn đá là: \(80.50.37,5 = 150\,000\left( {c{m^3}} \right)\)
Thể tích của hòn đá là: \(150\,000 - 140\,000 = 10000\left( {c{m^3}} \right) = 0,01\,\left( {{m^3}} \right)\)
Bài 5
Phương pháp:
Gọi số tiền thưởng của ba công nhân lần lượt là \(x;y;z{\kern 1pt} \left( {x;y;z > 0} \right).\)
Áp dụng tính chất tỉ lệ thuận và tính chất dãy tỉ số bằng nhau.
Cách giải:
Gọi số tiền thưởng của ba công nhân lần lượt là \(x;y;z{\kern 1pt} \left( {x;y;z > 0} \right).\)
Vì năng suất lao động tương ứng tỉ lệ với 3; 5; 7 nên số tiền thưởng cũng tỉ lệ thuận với 3; 5; 7
Ta có \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{7}\) và \(x + y = 5,6\)
Áp dụng dãy tỉ số bằng nhau ta có \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{7} = \dfrac{{x + y}}{{3 + 5}} = \dfrac{{5,6}}{8} = 0,7\,\,\,\,\,\,\,{\kern 1pt} \left( 1 \right)\)
Lại có \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{7} = \dfrac{{x + y + z}}{{3 + 5 + 7}} = \dfrac{{x + y + z}}{{15}}{\kern 1pt} \,\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(\dfrac{{x + y + z}}{{15}} = 0,7 \Rightarrow x + y + z = 10,5.\)
Tổng số tiền ba người được thưởng là 10,5 triệu.
Bài 6
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Theo giả thiết: \(\dfrac{x}{{2018}} = \dfrac{y}{{2019}} = \dfrac{z}{{2020}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{{2018}} = \dfrac{y}{{2019}} = \dfrac{z}{{2020}} = \dfrac{{x - y}}{{ - 1}} = \dfrac{{x - z}}{{ - 2}} = \dfrac{{y - z}}{{ - 1}}\)
Khi đó, \(x - y = \dfrac{1}{2}\left( {x - z} \right)\) và \(y - z = \dfrac{1}{2}\left( {x - z} \right)\)
Xét vế phải của đẳng thức:
\(\begin{array}{l}VP = 8{\left( {x - y} \right)^2}\left( {y - z} \right)\\\,\,\,\,\,\,\,\,\, = 8.{\left[ {\dfrac{1}{2}\left( {x - z} \right)} \right]^2}.\dfrac{1}{2}\left( {x - z} \right)\\\,\,\,\,\,\,\,\,\, = 8.\dfrac{1}{4}{\left( {x - z} \right)^2}.\dfrac{1}{2}\left( {x - z} \right)\\\,\,\,\,\,\,\,\,\, = {\left( {x - z} \right)^3}\\\,\,\,\,\,\,\,\,\, = VT\end{array}\)
\( \Rightarrow \) Đpcm
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra học kì 1 Toán 7 - Đề số 8 - Cánh diều timdapan.com"