Đề kiểm tra học kì 1 Toán 7 - Đề số 4 - Cánh diều

Đề bài

Phần I: Trắc nghiệm (3 điểm).

Câu 1: Cách viết nào dưới đây không đúng?

     A. \(\sqrt {49}  = 7\)            B. \( - \sqrt {49}  =  - 7\)       C. \(\sqrt {49}  =  \pm 7\)    D. \(\sqrt {{{\left( { - 7} \right)}^2}}  = 7\)

Câu 2: \({\left( { - 3} \right)^4}\) có giá trị bằng:

     A. -81                                B. 12                                  C. 81                                  D. -12

Câu 3: Nếu 15 lít dầu hỏa nặng 12kg thì 24 kg dầu hỏa chứa đầy trong thùng:

     A. 27 lít                             B. 7,5 lít                             C. 15 lít                             D. 30 lít

Câu 4: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \( - 0,75\)?

     A. \(\dfrac{{ - 6}}{2}\)          B. \(\dfrac{8}{{ - 6}}\)          C. \(\dfrac{9}{{ - 12}}\)        D. \(\dfrac{{ - 12}}{9}\)

Câu 5: Nếu góc xOy có số đo bằng 47⁰ thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu?

     A. 74                                  B. 47                                  C. 43                                  D. 133

Câu 6: Làm tròn số 1,7846 đến hàng phần nghìn ta được số nào

     A. 1,78                               B. 1,8                                 C. 1,784                             D. 1,785

Câu 7: Cho \(\left| a \right| = \dfrac{2}{5}\) thì:

     A. \(a = \dfrac{2}{5}\)         B. \(a =  - \dfrac{2}{5}\)       C. \(a = \dfrac{2}{5}\) hoặc \(a =  - \dfrac{2}{5}\)     D. \(a = \dfrac{2}{5}\) hoặc a = 1

Câu 8: Cho hình vẽ. Số đo của góc \(\angle DCB\) trong hình vẽ bên là:

  

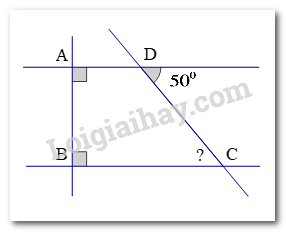
     A. 40                                  B. 50                                  C. 90                                  D. 140

Câu 9: Nếu a\( \bot \)b và b//c thì:

     A. \(a\parallel b\)               B. \(a \bot c\)                     C. \(b \bot c\)                     D. \(a\parallel b\parallel c\)

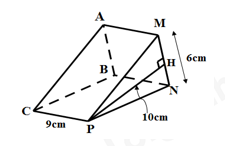
Câu 10: Tính thể tích của khối lăng trụ đứng ABC. MNP ở hình vẽ sau, trong đó PC = 9cm, MN = 6cm, PH = 10cm.

 

     A. 30                                  B. 270                                C. 540                                D. 135

Phần II: Tự luận (7 điểm).

Câu 1: (2 điểm) Thực hiện phép tính sau:

     a.  \(\dfrac{9}{{17}} + \dfrac{8}{9}:\dfrac{{17}}{9}\)                                                                 b. \({\left( {\dfrac{2}{3}} \right)^2} + \left| {\left( { - 2\dfrac{1}{3}} \right)} \right| - \sqrt {\dfrac{{49}}{{64}}} \)                                              

     c. \(\left( {\dfrac{{15}}{{11}} - \dfrac{4}{{13}}} \right):\dfrac{{12}}{{17}} + \left( {\dfrac{7}{{11}} - \dfrac{9}{{13}}} \right):\dfrac{{12}}{{17}}\)                                                   d. \(\dfrac{{{{20}^3}.{{( - 49)}^2}}}{{{{14}^3}{{.5}^4}}}\)                                                 

Câu 2: (1,5 điểm) Tìm x

a.  \(1\dfrac{3}{2} - x = \dfrac{5}{3}\)                                                             b. \(x:\dfrac{4}{3} = 2\dfrac{1}{4}:\dfrac{1}{3}\)                     c. \(\left| {x - \dfrac{1}{2}} \right| - \sqrt {25}  =  - 2\)                    

Câu 3: (1,5 điểm) Ba đơn vị kinh doanh gốp vốn theo tỉ lệ 3; 5; 7. Hỏi mỗi đơn vị chia bao nhiêu lãi nếu tổng số tiền lãi là 450 triệu đồng và tiền lãi được chia tỉ lệ thuận với số vốn đã góp.

Câu 4: (1,5 điểm) Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75m. Hỏi người thợ phải dung bao nhiêu viên gạch men hình chữ nhật để lát đáy và xung quanh thành bể đó? Biết rằng diện tích mạch vữa lát không đáng kể và mỗi viên gạch có chiều dài 25cm, chiều rộng 20cm.

Câu 5: (0,5 điểm) Tìm x biết: \(\left| {2x - 1} \right| + \left| {1 - 2x} \right| = 8\)

---

Lời giải

I. Phần trắc nghiệm (3 điểm)

Câu 1

Phương pháp:

Giá trị của căn bậc hai số học là 1 số không âm.

Cách giải:

\(\sqrt {49}  =  \pm 7\)là sai.

Chọn C.

Câu 2

Phương pháp:

\({\left( { - 3} \right)^4}\)=(-3) (-3) (-3) (-3)

Cách giải:

\({\left( { - 3} \right)^4}\)=81

Chọn C.

Câu 3

Phương pháp:

Số lít dầu hỏa và cân nặng là 2 đại lượng tỉ lệ thuận.

Cách giải:

Số lít dầu hỏa và cân nặng là 2 đại lượng tỉ lệ thuận nên \(\dfrac{{15}}{x} = \dfrac{{12}}{{24}} \Rightarrow 15.24 = 12.x \Rightarrow x = 30\)

Chọn D.

Câu 4

Phương pháp:

Rút gọn từng phân số

Cách giải:

Ta có: \( - 0,75 = \dfrac{{ - 75}}{{100}} = \dfrac{{\left( { - 75} \right):25}}{{100:25}} = \dfrac{{ - 3}}{4}\)

\(\dfrac{9}{{ - 12}} = \dfrac{{3.3}}{{ - 4.3}} = \dfrac{{ - 3}}{4}\)

Chọn D.

Câu 5

Phương pháp:

Hai góc đối đỉnh có số đo bằng nhau.

Cách giải:

Hai góc đối đỉnh có số đo bằng nhau nên \(\widehat {xOy} = 47^\circ \).

Chọn B.

Câu 6

Phương pháp:

Hàng phần nghìn là số 4 có hàng phần chục nghìn là số 6 lớn hơn 5

Cách giải:

Hàng phần nghìn là số 4 có hàng phần chục nghìn là số 6 lớn hơn 5 nên ta làm tròn thành 1,785

Chọn D.

Câu 7

Phương pháp:

\(\left| {\dfrac{2}{5}} \right| = \dfrac{2}{5}\) và \(\left| {\dfrac{{ - 2}}{5}} \right| = \dfrac{2}{5}\)

Cách giải:

\(\left| a \right| = \dfrac{2}{5}\) suy ra \(a = \dfrac{2}{5}\) hoặc \(a =  - \dfrac{2}{5}\)

Chọn C.

Câu 8

Phương pháp:

\(\angle DCB\)và góc \(\angle D\) là 2 góc so le trong

Cách giải:

\(\angle DCB\)và góc \(\angle D\) là 2 góc so le trong nên \(\angle DCB = {50^0}\)

Chọn B.

Câu 9

Phương pháp:

Từ vuông góc đến song song.

Cách giải:

\(b\parallel c\) mà \(a \bot b\) nên \(a \bot c\)

Chọn B.

Câu 10

Phương pháp:

Thể tích của khối lăng trụ đứng bằng chiều cao nhân diện tích đáy.

Cách giải:

Hình lăng trụ đứng tam giác ABC.MNP có chiều cao là \(CP = 9cm.\)
Diện tích tam giác MNP là:\({S_{\Delta MNP}} = \dfrac{1}{2}MN.PH = \dfrac{1}{2}.6.10 = 30{\mkern 1mu} (c{m^2}).\)
Thể tích của khối lăng trụ đứng ABC.MNP là: \(V = {S_{\Delta MNP}}.CP = 30.9 = 270{\mkern 1mu} (c{m^3}).\)

Chọn B.

II. Phần tự luận (7 điểm)                               

Câu 1

Phương pháp:

Thực hiện phép tính theo thứ tự thực hiện phép tính.

Cách giải:

a.  \(\dfrac{9}{{17}} + \dfrac{8}{9}:\dfrac{{17}}{9}\)\( = \dfrac{9}{{17}} + \dfrac{8}{9}.\dfrac{9}{{17}} = \,\,\dfrac{9}{{17}}\,\, + \dfrac{8}{{17}}\, = \dfrac{{17}}{{17}} = 1\)

b. \({\left( {\dfrac{2}{3}} \right)^2} + \left| {\left( { - 2\dfrac{1}{3}} \right)} \right| - \sqrt {\dfrac{{49}}{{64}}} \)\( = \dfrac{4}{9} + \dfrac{7}{3} - \dfrac{7}{8} = \dfrac{{32 + 168 - 63}}{{72}} = \dfrac{{137}}{{72}}\) 

c. \(\left( {\dfrac{{15}}{{11}} - \dfrac{4}{{13}}} \right):\dfrac{{12}}{{17}} + \left( {\dfrac{7}{{11}} - \dfrac{9}{{13}}} \right):\dfrac{{12}}{{17}}\)\( = \,\dfrac{{17}}{{12}}.\left( {\dfrac{{15}}{{11}} - \dfrac{4}{{13}} + \dfrac{7}{{11}} - \dfrac{9}{{13}}} \right) = \,\,\dfrac{{17}}{{12}}.\left( {\dfrac{{22}}{{11}} - \dfrac{{13}}{{13}}} \right) = \dfrac{{17}}{{12}}.(2 - 1) = \dfrac{{17}}{{12}}\)

d. \(\dfrac{{{{20}^3}.{{( - 49)}^2}}}{{{{14}^3}{{.5}^4}}}\)\( = \dfrac{{({2^6}{{.5}^3}).({7^{^4}})}}{{({2^3}{{.7}^3}){{.5}^4}}} = \dfrac{{{2^3}.7}}{5} = \dfrac{{56}}{5}\)

Câu 2

Phương pháp:

\(\left| x \right| = a\,\) với \((a > 0)\)\( \Leftrightarrow \left[ \begin{array}{l}x = a\\x =  - a\end{array} \right.\)

\({x^2} = a\,\)với \((a > 0)\) \( \Leftrightarrow \left[ \begin{array}{l}x = \sqrt a \\x =  - \sqrt a \end{array} \right.\)

Cách giải:

a. \(1\dfrac{3}{2} - x = \dfrac{5}{3} \Rightarrow \,x = \dfrac{5}{2} - \dfrac{5}{3} \Rightarrow \,x = \,\,\,\,\dfrac{5}{6}\)

b.\(\,x:\dfrac{4}{3} = 2\dfrac{1}{4}:\dfrac{1}{3} \Rightarrow x = \,\,\,\dfrac{9}{4}.\dfrac{3}{1}.\dfrac{4}{3} \Rightarrow \,x = \,\,\,\,\,\,\,\,\,9\)

c.\(\,\left| {x - \dfrac{1}{2}} \right| - \sqrt {25}  =  - 2 \Rightarrow \left[ \begin{array}{l}x - \dfrac{1}{2} = 3\\x - \dfrac{1}{2} =  - 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}x\,\, = \dfrac{7}{2}\\x\,\, = \dfrac{{ - 5}}{2}\end{array} \right.\)

Câu 3

Phương pháp:

Đưa bài toán về dãy tỉ số bằng nhau.

Cách giải:

Gọi a, b, c lần lượt là số tiền lãi của ba đơn vị nhận được (triệu đồng)

Ta có: Số tiền lãi tỉ lệ thuận với số vốn đã góp.Theo đề bài, ta có: \(\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{c}{7}\) và \(a + b + c = 450\)

Áp dụng tính chất dãy tỉ số bằng nhau:

\(\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{c}{7} = \dfrac{{a + b + c}}{{3 + 5 + 7}} = \dfrac{{450}}{{15}} = 30\)

\(\dfrac{a}{3} = 30 \Rightarrow a = 90;\,\,\,\dfrac{b}{5} = 30 \Rightarrow b = 150;\,\,\,\dfrac{c}{7} = 30 \Rightarrow c = 210\).

Vậy số tiền lãi của ba đơn vị nhận được lần lượt là: 90; 150; 210 (triệu đồng).

Câu 4

Phương pháp:

Tính diện tích xung quanh bể bơi, diện tích đáy bể, diện tích cần lát gạch, diện tích 1 viên gạch. Từ đó tính số viên gạch cần lát.

Cách giải:

Diện tích xung quanh của bể bơi là: \(2.\left( {12 + 5} \right).2,75 = 93,5\left( {{m^2}} \right)\)

Diện tích đáy bể bơi là: \(12.5 = 60\left( {{m^2}} \right)\)

Diện tích cần lát gạch là: \(93,5 + 60 = 153,5\left( {{m^2}} \right) = 1535000\left( {{m^2}} \right)\)

Diện tích một viên gạch lát là: \(25.20 = 500\left( {c{m^2}} \right)\)

Số viên gạch cần để lát bể bơi là: \(1535000:500 = 3070\)(viên gạch)

Câu 5

Phương pháp:

Dùng đẳng thức \(\left| a \right| = \left| { - a} \right|\).

Cách giải:

Vì 2x – 1 và 1 – 2x là hai số đối nhau, nên: \(\left| {2x - 1} \right| = \left| {1 - 2x} \right|\)

Từ (1) và (2) suy ra:

\(\begin{array}{l}2\left| {2x - 1} \right| = 8\\ \Leftrightarrow \left| {2x - 1} \right| = 4\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x - 1 = 4}\\{2x - 1 =  - 4}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{5}{2}}\\{x = \dfrac{{ - 3}}{2}}\end{array}} \right.\end{array}\)

Vậy \(x \in \left\{ {\dfrac{5}{2};\dfrac{{ - 3}}{2}} \right\}\).