Đề kiểm tra 15 phút - Đề số 5 - Bài 9 - Chương 3 - Hình học 9

Đề bài

Gọi M là một điểm nằm trên đường tròn (O). Vẽ đường tròn (O’) đường kính OM. Bán kính OA của (O) cắt (O’) tại B. Chứng minh rằng hai cung MA và MB bằng nhau.

Lời giải chi tiết

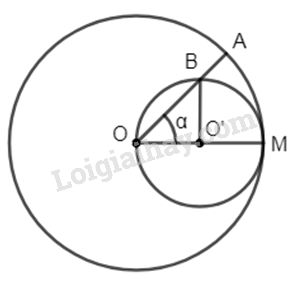
Đặt \(\widehat {MOA} = \alpha \)

\( \Rightarrow \widehat {MO'B} = 2\alpha \) ( góc ngoài của \(∆OO’B\))

Gọi \(l_1\) là độ dài cung MA của đường tròn (O), \({l_1} = \dfrac{{\pi .OM.\alpha } }{ {180}}\)

Độ dài cung MB của đường tròn (O’) bán kính \(\dfrac{{OM} }{ 2}\) :

Có \({l_2} = \dfrac{{\pi {{OM} \over 2}.2\alpha } }{ {180}} =\dfrac {{\pi OM\alpha } }{ {180}}\).

Vậy \({l_1} = {l_2}\) (đpcm).