Đề số 5 - Đề kiểm tra học kì 2 - Vật lí 12

Đề bài

Câu 1:

a)(1 điểm) Khảo sát sự biến thiên của điện tích trên hai bản tụ điện và sự biến thiên của cường độ dòng điện trong mạch dao động.

b)(1 điểm) Khảo sát năng lượng điện từ trong mạch dao động.

c)(1 điểm) Vì sao dao động trong mạch dao động lại tắt dần?

Câu 2: (2 điểm)

Cho một mạch dao động LC lí tưởng, gồm một tụ điện có điện dung \(C = 5\mu F\)  và cuộn cảm thuần có độ tự cảm L=50mH.

a)(0,5 điểm) Xác định tần số dao động điện từ trong mạch dao động.

b) 90,5 điểm) Tính năng lượng của mạch dao động khi biết hiệu điện thế cực đại trên tụ điện là 6V.

c)(1 điểm) Tìm năng lượng điện trường và năng lượng từ trường trong mạch khi biết hiệu điện thế trên tụ điện là 4V. Tính cường độ dòng điện I khi đó.

Câu 3: (2 điểm) Trong thí nghiệm giao thoa ánh sáng dùng hai khe Y-âng, biết D=1,2m, a=2mm. Nguồn điểm phát đồng thời hai bức xạ đơn sắc, bước sóng lần lượt là 660nm và 550nm. Tính khoảng cách từ vân sáng chính giữa đến vân sáng đầu tiên trên màn, cùng màu với nó.

Câu 4: (2 điểm) Trong thí nghiệm giao thoa ánh sáng với hai khe Y-âng, khoảng cách giữa hai khe là 1,5mm. Hai khe đặt cách màn ảnh bằng 2m. Chiếu ánh sáng đơn sắc có bước sóng \(\lambda  = 0,48\mu m.\)  Tìm khoảng cách giữa hai vân sáng liên tiếp và khoảng cách từ vân sáng trung tâm O đến vân sáng bậc 6.

Câu 5: (1 điểm) Hiệu điện thế giữa hai cực của một ống Rơn-ghen là 20kV. Giả sử electron bật ra từ cactot có vận tốc ban đầu bằng 0 thì bước sóng ngắn nhất của tia X mà ống Rơn-ghen có thể phát ra là bao nhiêu?

Lời giải chi tiết

Câu 1:

a) Khảo sát sự biến thiên của điện tích trên hai bản tụ điện và sự biến thiên của cường độ dòng điện trong mạch dao động.

- Mạch dao động (Hình bên)

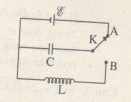
Mạch dao động gồm một tụ điện mắc với một cuộn cảm thành mạch kín.

Mạch dao động lí tưởng có điện trwor thuần bằng 0.

- Sự biến thiên điện tích của một bản tụ điện và suất điện động cảm ứng trên cuộn dây.

Điện tích (q) của một bản tụ điện và suất điện động cảm ứng (e) trên cuộn dây của mạch dao động lí tưởng biến thiên điều hòa.

Nếu chọn gốc thời gian (t = 0) là lúc tụ điện bắt đầu phóng điện, ta có:

q = q₀ và i = 0 suy ra: \(\varphi  = 0\)

Khi đó: \(q = {q_0}cos\omega t\)  và \(i = q' =  - {q_0}\omega \sin \omega  \)\(\,= {q_0}\omega cos\left( {\omega t + \dfrac{\pi }{2}} \right);\)\(\,{I_0} = {q_0}\omega \)

\(i = {I_0}cos\left( {\omega t + \dfrac{\pi }{2}} \right)\)  (i biến thiên điều hòa sớm pha \(\dfrac{\pi }{2}\)  so với q)

\(e = u = \dfrac{q}{C} = \dfrac{{{q_0}}}{C}cos(\omega t + \varphi )\)

Tần số góc riêng của mạch dao động: \(\omega  = \dfrac{1}{{\sqrt {LC} }}\)

Tần số riêng của mạch dao động: \(f = \dfrac{\omega }{{2\pi }} = \dfrac{1}{{2\pi \sqrt {LC} }}\)

Chu kì riêng của mạch dao động: \(T = \dfrac{1}{f} = 2\pi \sqrt {LC} \)

b) Khảo sát năng lượng điện từ trong mạch dao động.

- Năng lượng điện trường trong tụ điện:

\({{\rm{W}}_C} = \dfrac{1}{2}\dfrac{{{q^2}}}{C} = \dfrac{{q_0^2}}{{2C}}co{s^2}(\omega t + \varphi );\)\(\,{{\rm{W}}_{C(max)}} = \dfrac{{q_0^2}}{{2C}} = \dfrac{1}{2}{q_0}{U_0}\)

- Năng lượng từ trường trong cuộn cảm:

\(\begin{array}{l}{{\rm{W}}_L} = \dfrac{1}{2}L{i^2} = \dfrac{1}{2}q_0^2L{\omega ^2}{\sin ^2}(\omega t + \varphi );\\{{\rm{W}}_{L(max)}} = \dfrac{1}{2}LI_0^2 = \dfrac{1}{2}{q_0}{U_0}\end{array}\)

-Năng lượng điện từ trong mạch dao động:

\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_C} + {{\rm{W}}_L} = const\\{\rm{W}} = {{\rm{W}}_{C(max)}} = {{\rm{W}}_{L(max)}} \\\;\;\;\;\;= \dfrac{1}{2}{q_0}{U_0} = \dfrac{{q_0^2}}{{2C}} = \dfrac{1}{2}LI_0^2\end{array}\)

c) Vì sao dao động trong mạch dao động lại tắt dần?

Trong thực tế, trong mạch dao động LC luôn có điện trở thuần R làm tiêu hao điện năng, dẫn tới dao động bị tắt dần. Nếu R quá lớn, thì sự chuyển hóa điện từ trong mạch không còn là tuần hoàn nữa.

Câu 2:

\(\begin{array}{l}a)T = 2\pi \sqrt {LC}  = 2\pi \sqrt {{{5.10}^{ - 2}}{{.5.10}^{ - 6}}}\\\;\;\;\;\;\;\;  \approx 3,{15.10^{ - 3}}s\\b){\rm{W}} = \dfrac{1}{2}CU_0^2 = \dfrac{1}{2}{5.10^{ - 6}}{.6^2}\\\;\;\;\;\;\;\;\; = {9.10^{ - 5}}J\\c){{\rm{W}}_d} = \dfrac{1}{2}C{u^2} = \dfrac{1}{2}{.5.10^{ - 6}}{.4^2}\\\;\;\;\;\;\;\;\;\; = {4.10^{ - 5}}J\\{{\rm{W}}_t} = {\rm{W}} - {{\rm{W}}_d} = {5.10^{ - 5}}J\end{array}\)

Từ công thức: \({{\rm{W}}_t} = \dfrac{{L{i^2}}}{2}\)

\(\Rightarrow i = \sqrt {\dfrac{{2{{\rm{W}}_t}}}{L}}  = \sqrt {\dfrac{{{{2.5.10}^{ - 5}}}}{{{{5.10}^{ - 2}}}}}  \)\(\,= 4,{47.10^{ - 2}}A\)

Câu 3:

Vị trí trùng nhau của hai vân sáng ứng với hai bức xạ sẽ có màu cùng màu của vân trung tâm. Do đó ta có:

\({x_1} = {x_2} \Leftrightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} \)

\(\Leftrightarrow \dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}} = \dfrac{5}{6}\)

Khoảng cách ngắn nhất x giữa vân sáng có màu giống như màu của vân trung tâm, ứng với k₁=5 và k₂=6.

Khoảng cách từ vân sáng chính giữa đến vân sáng đầu tiên trên màn, cùng màu với nó là: \(x = {x_1} = \dfrac{{{k_1}{\lambda _1}D}}{a} = \dfrac{{5.0,{{66.10}^{ - 6}}.1,2}}{{{{2.10}^{ - 3}}}} \)\(\,= 2,64mm\)

Câu 4:

\(i = \dfrac{{0,{{48.10}^{ - 6}}.2}}{{1,{{5.10}^{ - 3}}}} = 0,64mm;\)

\({x_6} = 6i = 3,84mm\)

Câu 5:

\(eU = \dfrac{{hc}}{{{\lambda _{\min }}}}\)

\(\Rightarrow {\lambda _{\min }} = \dfrac{{hc}}{{eU}} = \dfrac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{1,{{6.10}^{ - 19}}{{.20.10}^3}}}\)\(\, = 0,{62.10^{ - 9}}m.\)