Câu 53 trang 60 Sách Bài tập Hình học 11 Nâng cao

Đề bài

Cho lăng trụ tam giác ABC.A’B’C’. Trên đường thẳng BA lấy một điểm M sao cho A nằm giữa B và M, \(MA = {1 \over 2}AB\)

a) Xác định thiết diện của hình lăng trụ khi cắt bởi mặt phẳng (P) qua M, B’ và trung điểm E của AC.

b) Tính tỉ số \({{BD} \over {CD}}\left( {D = BC \cap mp\left( {MB'E} \right)} \right)\).

Lời giải chi tiết

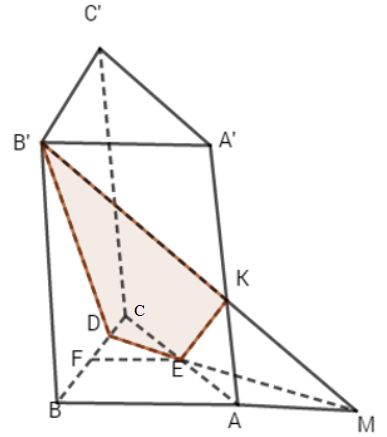
a) Trong mp(ABB’A’) nối M với B’ cắt AA’ tại K.

Trong mp(ABC) nối M với E cắt CB tại D.

Thiết diện là tứ giác DEKB’.

b) Kẻ EF // AB \(\left( {F \in CB} \right)\). Khi đó EF là đường trung bình của tam giác ABC và \({\rm{EF}} = {{AB} \over 2}\).

Xét tam giác DBM ta có:

\({{FD} \over {BD}} = {{EF} \over {BM}} = {1 \over 3}\)

Suy ra FD = \({1 \over 2}\)BF = FC, tức D là trung điểm FC.

Vậy \({{BD} \over {CD}} = 3\).