Câu 15 trang 28 SGK Đại số và Giải tích 11 Nâng cao

Đề bài

a. Vẽ đồ thị của hàm số \(y = \sin x\) rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng \((-π ; 4π)\) là nghiệm của mỗi phương trình sau :

1.  \(\sin x = - {{\sqrt 3 } \over 2}\)

2. \(\sin x = 1\)

b. Cũng câu hỏi tương tự cho hàm số \(y = \cos x\) đối với mỗi phương trình sau

1.  \(\cos x = {1 \over 2}\)

2. \(\cos x = -1\).

Lời giải chi tiết

a.  \(1/\,\,\sin x = - {{\sqrt 3 } \over 2} \Leftrightarrow \sin x = \sin \left( { - {\pi \over 3}} \right) \Leftrightarrow \left[ {\matrix{{x = - {\pi \over 3} + k2\pi } \cr {x = {{4\pi } \over 3} + k2\pi } \cr} } \right.\)

*Với \(x = - {\pi \over 3} + k2\pi \,\text{ và }\,x \in \left( { - \pi ;4\pi } \right)\) ta có nghiệm :

\({x_1} = - {\pi \over 3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_2} = {{5\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_3} = {{11\pi } \over 3}\)

* Với \(x = {{4\pi } \over 3} + k2\pi \,\text{ và }\,x \in \left( { - \pi ;4\pi } \right)\) ta có nghiệm :

\({x_4} = - {{2\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_5} = {{4\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_6} = {{10\pi } \over 3}\)

2/ \(\sin x = 1   \Leftrightarrow x = {\pi \over 2} + k2\pi \)

* Với \(x = {\pi \over 2} + k2\pi \,va\,x \in \left( { - \pi ;4\pi } \right)\) ta có nghiệm :

\({x_1} = {\pi \over 2};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_2} = {{5\pi } \over 2}.\)

Xem hình vẽ

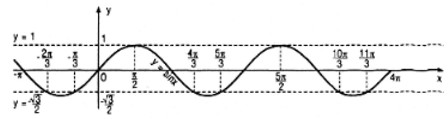
b. Tương tự câu a) ta có hình vẽ sau :

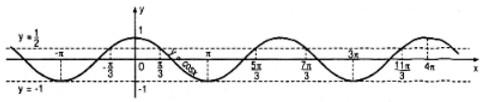
1. Nghiệm của phương trình \(\cos x = {1 \over 2}\) thuộc khoảng \((-π;4π)\) là :

\({x_1} = - {\pi \over 3};\,\,\,\,\,\,\,\,\,\,{x_2} = {\pi \over 3};\,\,\,\,\,\,\,\,\,\,\,{x_3} = {{5\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,{x_4} = {{7\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,\,{x_5} = {{11\pi } \over 3}\)

2. Nghiệm của phương trình \(\cos x = -1\) thuộc khoảng \((-π ; 4π)\) là :

\(x_1= -π\)       \(x_2 = π\)        \(x_3= 3π\)