Bài tập 16 trang 111 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Hãy tính thể tích và diện tích toàn phần của các hình không gian dưới đây.
Đề bài
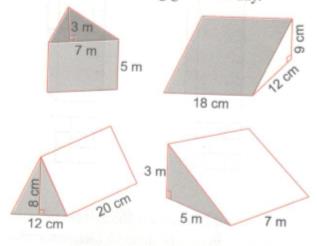
Hãy tính thể tích và diện tích toàn phần của các hình không gian dưới đây.
Lời giải chi tiết
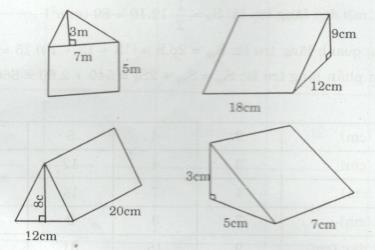
• Hình a là lăng trụ đứng: đáy là tam giác ABC vuông tại A, chiều cao của lăng trụ là 5cm
Diện tích tam giác đáy lăng trụ là: \({S_d} = {1 \over 2}.3.7 = 10,5({m^2})\)
Thế tích lăng trụ: \(V = S.h = 10,5.5 = 52,5({m^3})\)
∆ABC vuông tại A \( \Rightarrow A{B^2} + A{C^2} = B{C^2}\) (định lí Py-ta-go) \( \Rightarrow A{B^2} + A{C^2} = {7^2} = 49\)
Mặt khác \(AB.AC = AH.BC( = 2{S_{ABC}})\)
\(\Rightarrow AB.AC = 3.7 = 21\)
Ta có \({(AB + AC)^2} = A{B^2} + A{C^2} + 2AB.AC \)\(\,= 49 + 2.21 = 91 \)
\(\Rightarrow AB + AC = \sqrt {91} \)
Và \({(AB - AC)^2}\)\(\,= A{B^2} + A{C^2} - 2AB.AC \)\(\,= 49 - 2.21 = 7\)
\( \Rightarrow \left| {AB - AC} \right| = \sqrt 7 \)
\(\Rightarrow AC - AB = \sqrt 7 \)
Do đó \(AC = {{\sqrt {91} + \sqrt 7 } \over 2} \approx 6,09(cm)\) và \(AB = {{\sqrt {91} - \sqrt 7 } \over 2} \approx 3,45(cm)\)
Diện tích xung quanh lăng trụ là: \({S_{xq}} = 2ph = (6,09 + 3,45 + 7).5 = 82,7({m^2})\)
Diện tích toàn phần lăng trụ: \({S_{tp}} = {S_{xq}} + {S_{day}}.2 = 82,7 + 10,5.2 = 103,7({m^2})\)
• Hình b là lăng trụ đứng: đáy là tam giác vuông, chiều cao của lăng trụ là 18cm
∆ABC vuông tại B có \(A{C^2} = A{B^2} + B{C^2}\) (định lí Py-ta-go)
\( \Rightarrow A{C^2} = {9^2} + {12^2} \Rightarrow AC = 15(cm)\)
Diện tích tam giác đáy là: \({S_d} = {1 \over 2}.9.12 = 54(c{m^2})\)
Thế tích lăng trụ: \(V = S.h = 54.18 = 972(c{m^3})\)
Diện tích xung quanh lăng trụ là: \({S_{xq}} = 2p.h = (15 + 9 + 12).18 = 648(c{m^2})\)
Diện tích toàn phần lăng trụ: \({S_{tp}} = {S_{xq}} + 2{S_d} = 648 + 54.2 = 756(c{m^2})\)
• Hình c là lăng trụ đứng: đáy là tam giác ABC cân ở A, chiều cao của lăng trụ là 20cm
∆ABC cân ở A có AH là đường cao (gt) => AH là đường trung tuyến
=> H là trung điểm của BC \( \Rightarrow BH = {{BC} \over 2} = {{12} \over 2} = 6(cm)\)
∆ABH vuông tại H có: \(A{B^2} = A{H^2} + B{H^2}\) (định lí Py-ta-go)
\( \Rightarrow A{B^2} = {8^2} + {6^2} = {10^2}\)
\(\Rightarrow AB = 10(cm) \Rightarrow AC = AB = 10(cm)\)
Diện tích tam giác đáy là: \({S_d} = {1 \over 2}.8.12 = 48(c{m^2})\)
Thế tích lăng trụ: \(V = S.h = 48.20 = 960(c{m^3})\)
Diện tích xung quanh lăng trụ là: \({S_{xq}} = 2p.h = (10 + 10 + 12).20 = 640(c{m^2})\)
Diện tích toàn phần lăng trụ: \({S_{tp}} = {S_{xq}} + 2{S_d} = 640 + 2.48 = 736({m^2})\)
• Hình d là lăng trụ đứng: đáy là tam giác DEF vuông tại E, chiều cao của lăng trụ là 7m
∆DEF vuông tại E có: \(D{F^2} = D{E^2} + E{F^2}\) (định lí Py-ta-go)
\( \Rightarrow D{F^2} = {3^2} + {5^2} \Rightarrow D{F^2} = 34 \)
\(\Rightarrow DF = \sqrt {34} (m)\)
Diện tích tam giác đáy là: \({S_d} = {1 \over 2}.3.5 = 7,5({m^2})\)
Thế tích lăng trụ: \(V = S.h = 7,5.7 = 52,5(c{m^3})\)
Diện tích xung quanh lăng trụ là: \({S_{xq}} = 2p.h = (3 + 5 + \sqrt {34} ).7 \)\(\,= 56 + 7\sqrt {34} ({m^2})\)
Diện tích toàn phần lăng trụ: \({S_{tp}} = {S_{xq}} + 2{S_d} = 56 + 7\sqrt {34} + 7,5.2\)\(\, = 71 + 7\sqrt {34} ({m^2})\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập 16 trang 111 Tài liệu dạy – học Toán 8 tập 2 timdapan.com"