Bài 7. Đồ thị độ dịch chuyển - thời gian trang 34, 35, 36 Vật Lí 10 Kết nối tri thức
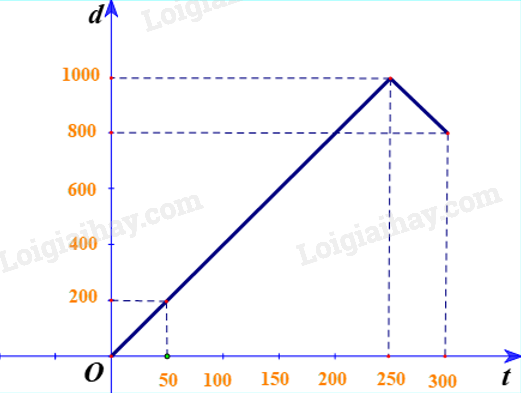
Hãy tính quãng đường đi được, độ dịch chuyển, tốc độ, vận tốc của bạn A khi đi từ nhà đến trường và khi đi từ trường đến siêu thị (Hình 7.1). Coi chuyển động của bạn A là chuyển động đều và biết cứ 100 m bạn A đi hết 25 s. Hãy vẽ đồ thị dịch chuyển – thời gian trong chuyển động của bạn A nêu ở trên theo trình tự sau đây. Hình 7.2 là đồ thị độ dịch chuyển – thời gian của một người đang bơi trong một bể bơi dài 50 m. Đồ thị này cho biết những gì về chuyển động của người đó. Số liệu về độ dịch chuy
Câu hỏi tr 34
| Hãy tính quãng đường đi được, độ dịch chuyển, tốc độ, vận tốc của bạn A khi đi từ nhà đến trường và khi đi từ trường đến siêu thị (Hình 7.1). Coi chuyển động của bạn A là chuyển động đều và biết cứ 100 m bạn A đi hết 25 s. |
Phương pháp giải:
- Xác định quãng đường, độ dịch chuyển, thời gian.
- Sử dụng công thức tốc độ trung bình, vận tốc trung bình.
Lời giải chi tiết:
* Đi từ nhà đến trường:
- Quãng đường đi được của bạn A là: \(s = 1000m\)
- Độ dịch chuyển:
Do chuyển động của bạn A từ nhà đến trường là chuyển động thẳng, không đổi chiều nên độ dịch chuyển bằng quãng đường đi được: \(s = d = 1000m\).
- Thời gian bạn A đi từ nhà đến trường là:
\(t = \frac{{1000.25}}{{100}} = 250{\rm{s}}\)
- Tốc độ: \(v = \frac{s}{t} = \frac{{1000}}{{250}} = 4\left( {m/s} \right)\)
- Vận tốc: \(v = \frac{d}{t} = \frac{{1000}}{{250}} = 4\left( {m/s} \right)\)
* Đi từ trường đến siêu thị:
- Quãng đường đi được của bạn A là:
\(s = 1000 - 800 = 200m\)
- Độ dịch chuyển: dịch chuyển ngược chiều dương nên \(d = - 200m\)
- Thời gian bạn A đi từ trường đến siêu thị là:
\(t = \frac{{200.25}}{{100}} = 50{\rm{s}}\)
- Tốc độ: \(v = \frac{s}{t} = \frac{{200}}{{50}} = 4\left( {m/s} \right)\)
- Vận tốc: \(v = \frac{d}{t} = - \frac{{200}}{{50}} = - 4\left( {m/s} \right)\)
HĐ 1
Hãy vẽ đồ thị dịch chuyển – thời gian trong chuyển động của bạn A nêu ở trên theo trình tự sau đây:
|
1. Lập bảng ghi số liệu vào vở.
2. Vẽ đồ thị: trên trục tung (trục độ dịch chuyển) 1 cm ứng với 200 m; trên trục hoành (trục thời gian) 1 cm ứng với 50 s. |
Phương pháp giải:
Dựa vào bảng số liệu để vẽ đồ thị.
Lời giải chi tiết:
1.
Lập bảng ghi số liệu.
|
Độ dịch chuyển (m) |
0 |
200 |
400 |
600 |
800 |
1000 |
800 |
|
Thời gian (s) |
0 |
50 |
100 |
150 |
200 |
250 |
300 |
2.
Vẽ đồ thị:
Từ bảng số liệu ta vẽ được đồ thị như hình sau:
HĐ 2
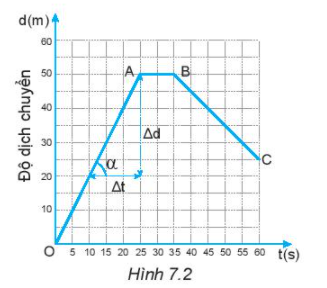
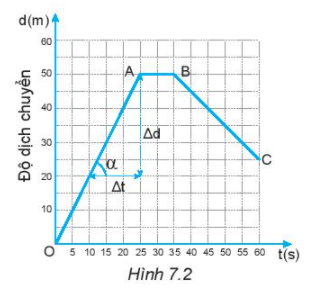
Hình 7.2 là đồ thị độ dịch chuyển – thời gian của một người đang bơi trong một bể bơi dài 50 m. Đồ thị này cho biết những gì về chuyển động của người đó?
|
1. Trong 25 giây đầu mỗi giây người đó bơi được bao nhiêu mét? Tính vận tốc của người đó ra m/s 2. Từ giây nào đến giây nào người đó không bơi? 3. Từ giây 35 đến giây 60 người đó bơi theo chiều nào? 4. Trong 20 giây cuối cùng, mỗi giây người đó bơi được bao nhiêu mét? Tính vận tốc của người đó ra m/s. 5. Xác định độ dịch chuyển và vận tốc của người đó khi bơi từ B đến C. 6. Xác định độ dịch chuyển và vận tốc của người đó trong cả quá trình bơi. |
Phương pháp giải:
- Dựa vào đồ thi hình 7.2.
- Sử dụng các công thức xác định tốc độ, vận tốc.
Lời giải chi tiết:
1.
Từ đồ thị ta thấy, trong 25s đầu người đó chuyển động thẳng từ O – A và không đổi chiều, độ dịch chuyển trong 25 s đầu là 50 m.
Suy ra: Mỗi giây người đó bơi được: \(\frac{{50}}{{25}} = 2\left( m \right)\)
Vận tốc của người đó là: \(v = \frac{d}{t} = \frac{{50}}{{25}} = 2\left( {m/s} \right)\)
2.
Từ A – B: người đó không bơi => Người đó không bơi từ giây 25 đến giây 35.
3.
Từ giây 35 đến giây 60 người đó bơi ngược chiều dương.
4.
Từ đồ thị ta thấy:
- Giây thứ 40 có d1 = 45 m
- Giây thứ 60 có d2 = 25 m
=> Trong 20 s cuối, mỗi giây người đó bơi được \(\frac{{\left| {25 - 45} \right|}}{{20}} = 1\left( m \right)\)
- Vận tốc của người đó là: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{{d_2} - {d_1}}}{{\Delta t}} = \frac{{25 - 45}}{{20}} = - 1\left( {m/s} \right)\)
5.
- Tại B: \({d_1} = 50m;\,{t_1} = 35s\)
- Tại C: \({d_2} = 25m;\,{t_2} = 60\,s\)
Từ B -> C, độ dịch chuyển là:
\(\Delta d = {d_2} - {d_1} = 25 - 50 = - 25m\)
Vận tốc của người đó khi bơi từ B -> C là:
\(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{ - 25}}{{60 - 35}} = - 1\left( {m/s} \right)\)
6.
Độ dịch chuyển của người đó trong cả quá trình bơi là:
\(\Delta d = 25m\)
Vận tốc của người đó trong cả quá trình bơi là:
\(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{25}}{{60}} = \frac{5}{{12}} \approx 0,417\left( {m/s} \right)\)
CH
|
Hãy xác định vận tốc và tốc độ của người bơi từ giây 45 đến giây 60 bằng đồ thị ở Hình 7.2
|
Phương pháp giải:
+ Vận tốc = Độ dịch chuyển : thời gian
+ Tốc độ = Quãng đường : thời gian
Lời giải chi tiết:
Từ giây 45 đến giây 60, ta có t = 60 - 45 = 15 (s)
Người đó không đổi chiều chuyển động từ giây 45 đến 60 nên ta có:
s = d = 40 - 25 = 15 (m).
=> Vận tốc (tốc độ) của người bơi là: \(v = \frac{d}{t} = \frac{{15}}{{15}} = 1(m/s)\).
Câu hỏi tr 36
|
1. Số liệu về độ dịch chuyển và thời gian của chuyển động thẳng của một xe ô tô đồ chơi chạy bằng pin được ghi trong bảng bên:
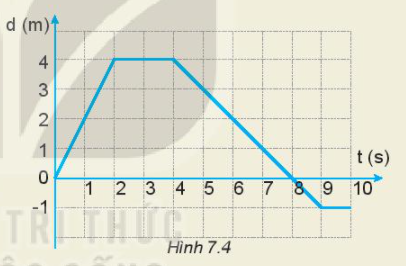
Dựa vào bảng này để: a) Vẽ đồ thị độ dịch chuyển – thời gian của chuyển động. b) Mô tả chuyển động của xe. c) Tính vận tốc của xe trong 3 s đầu. 2. Đồ thị độ dịch chuyển – thời gian trong chuyển động thẳng của một xe ô tô đồ chơi điều khiển từ xa được vẽ ở hình 7.4.
a) Mô tả chuyển động của xe. b) Xác định vị trí của xe so với điểm xuất phát của xe ở giây thứ 2, giây thứ 4, giây thứ 8 và giây thứ 10. c) Xác định tốc độ và vận tốc của xe trong 2 giây đầu, từ giây 2 đến giây 4 và từ giây 4 đến giây 8. d) Xác định quãng đường đi được và độ dịch chuyển của xe sau 10 giây chuyển động. Tại sao giá trị của chúng không giống nhau? |
Phương pháp giải:
- Dựa vào bảng số liệu để vẽ đồ thị và mô tả chuyển động.
- Sử dụng công thức tính vận tốc.
Lời giải chi tiết:
1.
a) Vẽ đồ thị độ dịch chuyển – thời gian:
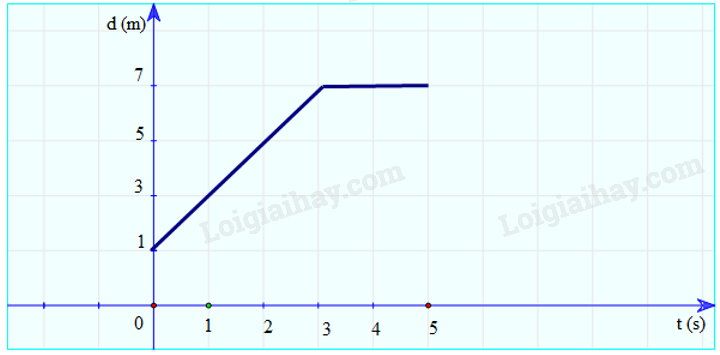
b) Mô tả chuyển động của xe:
- Từ 0 – 3 giây: xe chuyển động thẳng.
- Từ giây thứ 3 đến giây thứ 5: xe đứng yên (dừng lại)
c) Độ dịch chuyển của xe trong 3 giây đầu là:
\(d = 7 - 1 = 6m\)
Vận tốc của xe trong 3 giây đầu là:
\(v = \frac{{\Delta d}}{{\Delta t}} = \frac{6}{3} = 2\left( {m/s} \right)\)
2.
a) Mô tả chuyển động của xe:
- Trong 2 giây đầu: xe chuyển động thẳng
- Từ giây thứ 2 đến giây thứ 4: xe đứng yên
- Từ giây thứ 4 đến giây thứ 10: xe chuyển động thẳng theo chiều ngược lại.
- Từ giây thứ 9 đến giây thứ 10: xe dừng lại.
b)
- Ở giây thứ 2: xe ở vị trí cách điểm xuất phát 4 m.
- Ở giây thứ 4: xe ở vị trí cách điểm xuất phát 4 m
- Ở giây thứ 8: xe trở về vị trí xuất phát
- Ở giây thứ 10: xe ở vị trí cách điểm xuất phát 1 m theo chiều âm
c) Xác định tốc độ và vận tốc của xe:
- Trong 2 giây đầu, xe chuyển động thẳng, không đổi chiều nên tốc độ bằng vận tốc:
\(v = \frac{d}{t} = \frac{4}{2} = 2\left( {m/s} \right)\)
- Từ giây 2 đến giây 4: xe đứng yên nên vận tốc và tốc độ của xe đều bằng 0.
- Từ giây 4 đến giây 8:
+ Tốc độ: \(v = \frac{s}{t} = \frac{4}{4} = 1\left( {m/s} \right)\)
+ Vận tốc: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{0 - 4}}{{8 - 4}} = - 1\left( {m/s} \right)\)
d)
- Từ đồ thị, ta thấy quãng đường đi được của xe sau 10 giây chuyển động là:
\(s = 4 + 4 + 1 = 9\left( m \right)\)
- Độ dịch chuyển của xe sau 10 giây là:
\(d = - 1 - 4 + 4 = - 1\left( m \right)\)
=> Quãng đường và độ dịch chuyển của xe sau 10 giây không giống nhau vì xe chuyển động theo 2 chiều.
Lý thuyết
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7. Đồ thị độ dịch chuyển - thời gian trang 34, 35, 36 Vật Lí 10 Kết nối tri thức timdapan.com"