Bài 6 trang 147 Tài liệu dạy – học Toán 9 tập 1

Đề bài

Cho đường tròn (O) đường kính BC = 2R. Lấy điểm A thuộc đường tròn sao cho AB < AC. Tiếp tuyến tại A cắt tiếp tuyến tại B và C của đường tròn tại E và F.

a) Chứng minh rằng EF = EB + FC.

b) Chứng minh rằng \(BE.CF = {R^2}\).

c) Gọi M là giao điểm của EC và BF. Kẻ đường cao AH của tam giác ABC ( H thuộc BC). Chứng minh rằng ba điểm A, M, H thẳng hàng.

d) Trường hợp cho AB = R, chứng minh rằng tam giác AFC đều, tính theo R diện tích tam giác AFC.

Lời giải chi tiết

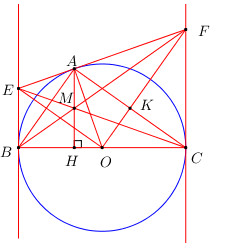
a) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có : \(EA = EB,\,\,FA = FC\)

\( \Rightarrow EF = EA + FA = EB + FC\).

b) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có:

\(OE\) là phân giác của \(\angle AOB\)

\(OF\) là phân giác của \(\angle AOC\).

Mà \(\angle AOB\)và \(\angle AOC\) là 2 góc kề bù

\( \Rightarrow OE \bot OF \Rightarrow \Delta OEF\) vuông tại O.

Áp dụng hệ thức lượng trong tam giác vuông \(OEF\) ta có : \(O{A^2} = EA.FA \Rightarrow {R^2} = BE.CF\).

c) Ta có : \(\dfrac{{FA}}{{EA}} = \dfrac{{FC}}{{EB}} = \dfrac{{FM}}{{BM}} \Rightarrow AM//BE\) (định lí Ta-lét đảo)

Mà \(BE \bot BC\,\,\left( {gt} \right) \Rightarrow AM \bot BC\)

Lại có \(AH \bot BC\,\,\left( {gt} \right) \Rightarrow A,M,H\) thẳng hàng (Tiên đề Ơ-clit).

d) Ta có \(OA = OB = AB = R \Rightarrow \Delta OAB\) đều \( \Rightarrow \angle OBA = {60^0}\).

Ta có : \(\left\{ \begin{array}{l}\angle OBA + \angle ACB = {90^0}\\\angle ACF + \angle ACB = {90^0}\end{array} \right.\)

\(\Rightarrow \angle ACF = \angle OBA = {60^0}\)

Xét tam giác \(ACF\) có :

\(\left\{ \begin{array}{l}FA = FC\,\,\left( {cmt} \right)\\\angle ACF = {60^0}\,\,\left( {cmt} \right)\end{array} \right. \)

\(\Rightarrow \Delta ACF\) đều,

\(A{C^2} = B{C^2} - A{B^2} = {\left( {2R} \right)^2} - {R^2}\)\(\, = 3{R^2}\)

\(\Rightarrow AC = R\sqrt 3 \).

\( \Rightarrow FA = FC = AC = R\sqrt 3 \).

Gọi \(K = AC \cap OF\) ta có :

\(OA = OC = R \Rightarrow O\) thuộc trung trực của \(AC\).

\(FA = FC\,\,\left( {cmt} \right) \Rightarrow F\) thuộc trung trực của \(AC\)

\( \Rightarrow OF\) là trung trực của \(AC \Rightarrow OF \bot AC\) tại \(K\) là trung điểm của \(AC\).

\( \Rightarrow AK = \dfrac{{AC}}{2} = \dfrac{{R\sqrt 3 }}{2}\).

Áp dụng định lí Pytago trong tam giác vuông \(FAK\) có :

\(F{K^2} = F{A^2} - A{K^2} \)\(\,= {\left( {R\sqrt 3 } \right)^2} - {\left( {\dfrac{{R\sqrt 3 }}{2}} \right)^2} = \dfrac{{9{R^2}}}{4}\)

\(\Rightarrow FK = \dfrac{{3R}}{2}\)

Vậy \({S_{\Delta ACF}} = \dfrac{1}{2}FK.AC = \dfrac{1}{2}.\dfrac{{3R}}{2}.R\sqrt 3 \)\(\, = \dfrac{{3{R^2}\sqrt 3 }}{4}\).