Bài 3 trang 147 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Từ điểm M ngoài đường tròn (O ; R) kẻ tiếp tuyến MA, MB với đường tròn (O) ( A, B là hai tiếp điểm).
Đề bài
Từ điểm M ngoài đường tròn (O ; R) kẻ tiếp tuyến MA, MB với đường tròn (O) ( A, B là hai tiếp điểm).
a) Chứng minh rằng OM là trung trực của AB.
b) Kẻ đường kính BD của đường tròn (O). Chứng minh rằng AD//MO.
c) Gọi N là giao điểm của MO với đường tròn (O) ( N nằm giữa M và O). Đường thẳng BN cắt đường thẳng DA tại E. Gọi K là giao điểm của AB với DN. Chứng minh rằng \(EK \bot DB.\)
Phương pháp giải - Xem chi tiết
a) Sử dụng định lí: Điểm cách đều 2 đầu mút của một đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó.
b) Chứng minh AD và MO cùng vuông góc với AB.
c) Chứng minh \(K\) là trực tâm của \(\Delta BDE\).
Lời giải chi tiết
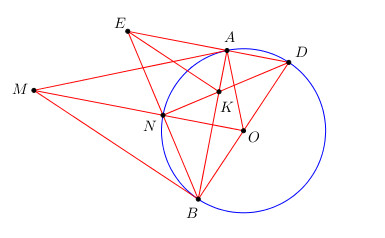
a) Ta có \(OA = OB = R \Rightarrow O\) thuộc trung trực của \(AB\).
\(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\).
Do đó \(OM\) là trung trực của \(AB\).
b) Do \(A\) thuộc đường tròn đường kính \(BD\) nên \(\angle BAD = {90^0} \Rightarrow AB \bot AD\).
Do \(OM\) là trung trực của \(AB\,\,\left( {cmt} \right) \Rightarrow OM \bot AB\)
\( \Rightarrow AD//OM\)(cùng vuông góc với AB).
c) Ta có \(N\) thuộc đường tròn đường kính \(BD \Rightarrow \angle BND = {90^0} \Rightarrow DN \bot BN\) hay \(DN \bot BE\).
Xét \(\Delta BDE\) có \(\left\{ \begin{array}{l}DN \bot BE\\AB \bot DE\\AB \cap DN = K\end{array} \right. \Rightarrow K\) là trực tâm tam giác \(BDE\).
Vậy \(EK \bot BD\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 147 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







