Bài 58 trang 56 SGK giải tích 12 nâng cao

LG a

Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = {{2x - 1} \over {x + 1}}\)

Giải chi tiết:

Tập xác đinh: \(D = R\backslash \left\{ { - 1} \right\}\)

\(y' = {3 \over {{{(x + 1)}^2}}}>0\,\,\forall x\in D\)

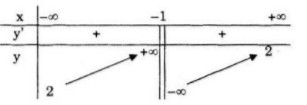
Hàm số đồng biến trên khoảng \(( - \infty ; - 1)\) và \(( - 1; + \infty )\)

Hàm số không có cực trị

Giới hạn

\(\mathop {\lim }\limits_{x \to  \pm \infty } y = 2\) 

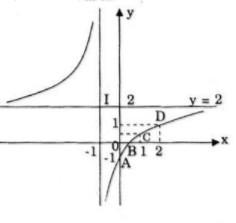
Tiệm cận đứng \(y=2\)

\(\eqalign{
& \mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \cr 
& \mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \cr} \)

Tiệm cận đứng: \(x=-1\)

Bảng biến thiên:

Đồ thị giao \(Ox\) tại điểm \(\left( {{1 \over 2};0} \right)\)

Đồ thị giao \(Oy\) tại điểm \((0;-1)\)

LG b

Với các giá nào của \(m\), đường thẳng \(\left( {{d_m}} \right)\) đi qua điểm \(A(-2;2)\) và có hệ số góc \(m\) cắt đồ thị của hàm số đã cho:
• Tại hai điểm phân biệt?
• Tại hai điểm thuộc hai nhánh của đồ thị?

Giải chi tiết:

Phương trình đường thẳng \(\left( {{d_m}} \right)\) qua điểm \(A(-2;2)\) có hệ số góc \(m\) là:

\(y - 2 = m\left( {x + 2} \right)\,\,\,\,hay\,\,\,\,y = mx + 2m + 2\)

Hoành độ giao điểm của đường thẳng \(\left( {{d_m}} \right)\) và đường cong đã cho là nghiệm phương trình:

\(\eqalign{
& \,\,\,\,\,mx + 2m + 2 = {{2x - 1} \over {x + 1}} \cr 
& \Leftrightarrow \left( {mx + 2m + 2} \right)\left( {x + 1} \right) = 2x - 1\,\,\,\,\,\left( 1 \right) \cr 
& \Leftrightarrow f\left( x \right) = m{x^2} + 3mx + 2m + 3 = 0\,\,\,\left( 2 \right) \cr} \)

(vì \(x = -1\) không là nghiệm của (1))

• Đường thẳng \(\left( {{d_m}} \right)\) cắt đường cong tại hai điểm phân biệt khi và chỉ khi phương trình \((2)\) có hai nghiệm phân biệt, tức là

\(\left\{ \matrix{
m \ne 0 \hfill \cr 
\Delta = {m^2} - 12m > 0 \hfill \cr} \right. \Leftrightarrow m < 0\,\,\text{ hoặc }\,m > 12\,\,\,\left( * \right)\)

• Hai nhánh của đường cong nằm về hai phía của đường tiệm cận đứng \(x = -1\) của đồ thị.
Đường thẳng \(\left( {{d_m}} \right)\) cắt đường cong tại hai điểm thuộc hai nhánh của nó khi và chỉ khi (1) có hai nghiệm \({x_1},\,{x_2}\) thỏa mãn \({x_1} <  - 1 < {x_2}\)

\(\eqalign{
& \Leftrightarrow {x_1} + 1 < 0 < {x_2} + 1\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) < 0 \cr 
& \Leftrightarrow {x_1}.{x_2} + {x_1} + {x_2} + 1 < 0 \Leftrightarrow {{2m + 3} \over m} - {{3m} \over m} + 1 < 0 \cr 
& \Leftrightarrow {3 \over m} < 0\,\text{(thỏa mãn diều kiện (*))} \cr} \)

Vậy với \(m < 0\) thì \(\left( {{d_m}} \right)\) cắt (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị.