Bài 5 trang 63 Hình học 12 Nâng cao

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\), \(AB = c,\,AC = b\) . Gọi \({V_1},{V_2},{V_3}\)  là thể tích các khối tròn xoay sinh bởi tam giác đó (kê cả các điểm trong) khi lần lượt quay quanh \(AB, AC, BC\).

a) Tính \({V_1},{V_2},{V_3}\) theo \(b, c\).

b) Chứng minh rằng \({1 \over {V_3^2}} = {1 \over {V_1^2}} + {1 \over {V_2^2}}\)

Lời giải chi tiết

Giải

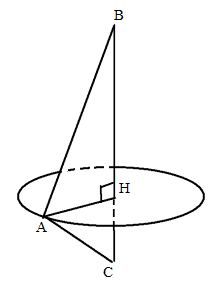
a) Khi quay tam giác \(ABC\) quanh \(AB\) ta được khối nón có chiều cao \(AB = c\) và bán kính đáy \(AC = b\) nên có thể tích \(V_1 = {1 \over 3}\pi c{b^2}\)

Tương tự khi quay tam giác \(ABC\) quanh \(AC\) ta được khối nón có thể tích \({V_2} = {1 \over 3}\pi b{c^2}\)

Gọi \(AH\) là chiều cao của tam giác \(ABC\). Khi quay tam giác \(ABC\) quanh \(BC\) ta được hai khối nón sinh bởi hai tam giác \(ABH\) và \(ACH\).

Khi đó ta có 
\({V_3} = {1 \over 3}\pi A{H^2}.BH + {1 \over 3}\pi A{H^2}.CH = {1 \over 3}\pi AH.BC = {1 \over 3}\pi {\left( {{{bc} \over {\sqrt {{b^2} + {c^2}} }}} \right)^2}\sqrt {{b^2} + {c^2}}  = {1 \over 3}{{\pi {b^2}{c^2}} \over {\sqrt {{b^2} + {c^2}} }}\)

b) Ta có: \({1 \over {V_3^2}} = {{9\left( {{b^2} + {c^2}} \right)} \over {\pi {b^4}{c^4}}}\)

\({1 \over {V_1^2}} + {1 \over {V_2^2}} = {9 \over {\pi {c^2}{b^4}}} + {9 \over {\pi {b^2}{c^4}}} = {{9\left( {{a^2} + {b^2}} \right)} \over {\pi {b^4}{c^4}}} = {1 \over {V_3^2}}\)