Bài 2 trang 63 SGK Hình học 12 Nâng cao

Đề bài

Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp \(S.ABC\), biết \(SA = SB = SC = a\), \(\widehat {ASB} = {60^0},\widehat {BSC} = {90^0},\widehat {CSA} = {120^0}\).

Lời giải chi tiết

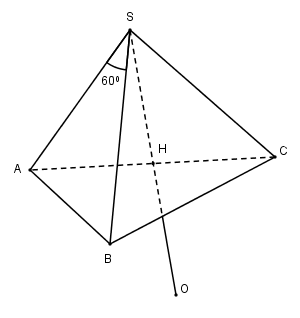
Áp dụng định lí Cosin trong tam giác \(SAB, SAC\) ta có:

\(\eqalign{
& A{B^2} = S{A^2} + S{B^2} - 2SA.SB.\cos {60^0} \cr 
& = {a^2} + {a^2} - 2{a^2}.{1 \over 2} = {a^2} \Rightarrow AB = a \cr 
& A{C^2} = S{A^2} + S{C^2} - 2SA.SC.\cos {120^0} \cr 
& = {a^2} + {a^2} - 2{a^2}\left( { - {1 \over 2}} \right) = 3{a^2} \Rightarrow AC = a\sqrt 3 \cr} \)

Trong tam giác vuông \(SBC\) có: \(B{C^2} = S{B^2} + S{C^2} = 2{a^2} \Rightarrow BC = a\sqrt 2 \)

Ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow \Delta ABC\) vuông tại \(B\).

Gọi \(H\) là trung điểm của \(AC\) thì \(H\) là tâm đường tròn ngoại tiếp tam giác ABC.

Vì \(SA = SB = SC\) nên \(SH \bot mp\left( {ABC} \right)\)

Và \(S{H^2} = S{C^2} - H{C^2} = {a^2} - {\left( {{{a\sqrt 3 } \over 2}} \right)^2} = {{{a^2}} \over 4} \Rightarrow SH = {a \over 2}\)

Gọi \(O\) là điểm đối xứng của \(S\) qua \(H\) thì \(SO = OA = OB = OC = a\) nên mặt cầu ngoại tiếp hình chóp \(S.ABC\) có tâm \(O\) và bán kính \(R = a\).