Bài 5 trang 234 SGK Vật lí 11 Nâng cao

Một lăng kính thuỷ tinh có chiết suất n = 1,5; tiết diện chính là một tam giác đều, được đặt trong không khí.

a) Tính góc lệch của tia sáng qua lăng kính khi góc tới là 30°.

b) Vẽ đường đi tia sáng và tính góc mà tia ló hợp với tia tới trong trường hợp tia tới vuông góc với mặt bên của lăng kính.

Giải

a) Ta có A = 60°, n = 1,5; lăng kính đặt trong không khí.

Theo giả thiết i = 30° \(\Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{{\mathop{\rm s}\nolimits} {\rm{ini}}} \over n} = {{\sin {{30}^0}} \over {1,5}} = 0,333 \Rightarrow r = {19^0}28'\)

Ta có: r' = A - r = 60 - 19°28' = 40°32'

\(\Rightarrow\) \(\sin i' = n\sin r' \)= 1,5sin40°32' = 0,975 \(\Rightarrow\) i' = 77°

Vậy góc lệch D = i + i' - A = 30° + 77° - 60° = 47°

b)

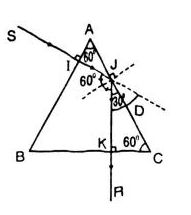
Trường hợp cho tia tới SI vuông góc với mặt bên lăng kính

 Tia sáng đi từ không khí vào lăng kính:

 n₁= 1, n₂ = 1,5

\(SI \bot AB\) \(\Rightarrow\) i = 0°

\( \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{\sin i} \over n_2} = {0 \over {1,5}} = 0 \Rightarrow r = 0\)

Tia IJ truyền thẳng đến mặt AC.

Tia sáng đi từ lăng kính ra không khí:

n₁ = 1,5, n₂ = 1

Ta có: \(\sin {i_{gh}} = {{{n_2}} \over {{n_1}}} = {1 \over {1,5}} \Rightarrow {i_{gh}} = {42^{0.}}\)

Góc tới i = 60° >i_gh nên có sự phản xạ toàn phần, tia JK là tia phản xạ.

Tia sáng đi từ lăng kính ra không khí: n₁ = 1,5, n₂ = 1

Ta có tia tới \(JK \bot BC\) nên i = 0 \(\Rightarrow\) r = 0

Tia ló KR truyền thẳng ra ngoài không khí

Dựa vào hinh vẽ ta tính được góc lệch D = 60°.