Bài 5 trang 122 SGK Hình học 12 Nâng cao
Cho hình vuông ABCD nội tiếp đường tròn (O; R). Gọi H là hình gồm các điểm của hình tròn (O; R) nhưng không nằm trong hình vuông. Tính thể tích hình tròn xoay sinh bởi hình H khi quay quanh đường thẳng chứa một đường chéo của hình vuông.
Đề bài
Cho hình vuông ABCD nội tiếp đường tròn (O; R). Gọi H là hình gồm các điểm của hình tròn (O; R) nhưng không nằm trong hình vuông. Tính thể tích hình tròn xoay sinh bởi hình H khi quay quanh đường thẳng chứa một đường chéo của hình vuông.
Lời giải chi tiết
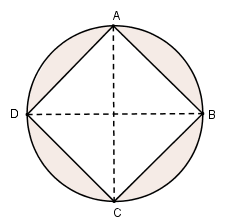
Khi quay quanh đường chéo AC thì:
+ hình tròn (O, R) sinh ra khối cầu (S) có thể tích \({V_{\left( S \right)}} = \frac{4}{3}\pi {R^3}\)
+ đoạn thẳng BD sinh ra hình tròn (C)
+ hình vuông ABCD sinh ra hình tròn xoay K gồm hai hình nón có chung đáy là (C) với đỉnh là A và C có thể tích \({V_{\left( K \right)}} = 2.\frac{1}{3}\pi {R^2}.R = \frac{2}{3}\pi {R^3}\)
Do đó H sinh ra khối tròn xoay gồm những điểm thuộc hình cầu (S) nhưng không thuộc K và thể tích V của khối đó là:
\(V = {V_{\left( S \right)}} - {V_{\left( K \right)}} \) \(= {4 \over 3}\pi {R^3} - \frac{2}{3}\pi {R^3} = {2 \over 3}\pi {R^3}.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5 trang 122 SGK Hình học 12 Nâng cao timdapan.com"







