Bài 3 trang 119 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí tương đối của mỗi điểm
Đề bài
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí tương đối của mỗi điểm \(M( - 1;1),N(\sqrt 2 ; - \sqrt 2 ),P(1; - 2)\) đối với đường tròn (O;2).
Phương pháp giải - Xem chi tiết
Cho đường tròn \(\left( {O;R} \right)\) và điểm M.
+) Nếu \(OM < R \Rightarrow \) Điểm M nằm bên trong đường tròn.
+) Nếu \(OM = R \Rightarrow \) Điểm M nằm trên đường tròn.
+) Nếu \(OM > R \Rightarrow \) Điểm M nằm bên ngoài đường tròn.
Lời giải chi tiết
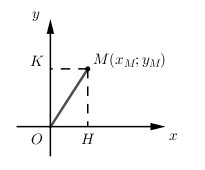
Cho điểm \(M\left( {x;y} \right)\). Gọi H, K lần lượt là hình chiếu của M trên Ox và Oy, khi đó ta có \(OH = \left| {{x_M}} \right|;\,\,OK = \left| {{y_M}} \right|\).
Do OHMK là hình chữ nhật (Tứ giác có 3 góc vuông) \( \Rightarrow MH = OK = \left| {{y_M}} \right|\).
Áp dụng định lí Pytago trong tam giác vuông OMH có:
\(O{M^2} = \sqrt {O{H^2} + H{M^2}} \)\(\, = \sqrt {{{\left| {{x_M}} \right|}^2} + {{\left| {{y_M}} \right|}^2}} = \sqrt {x_M^2 + y_M^2} \).
Áp dụng công thức trên ta tính được:
\(\begin{array}{l}OM = \sqrt {{{\left( { - 1} \right)}^2} + {1^2}} = \sqrt 2 \\ON = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( { - \sqrt 2 } \right)}^2}} = \sqrt 4 = 2\\OP = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \end{array}\)
+) Vì \(OM < R\,\,\left( {\sqrt 2 < 2} \right) \Rightarrow \) Điểm M nằm bên trong \(\left( {O;2} \right)\).
+) Vì \(ON = R\,\,\left( {2 = 2} \right) \Rightarrow \) Điểm N nằm trên \(\left( {O;2} \right)\).
+) Vì \(OP > R\,\,\left( {\sqrt 5 > 2} \right) \Rightarrow \) Điểm P nằm bên ngoài \(\left( {O;2} \right)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 119 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







