Bài 2 trang 116 Tài liệu dạy – học toán 6 tập 2
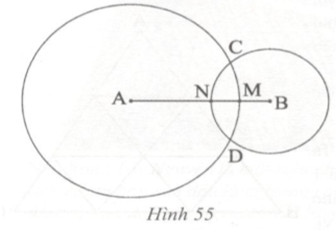
Giải bài tập Cho hai đường tròn (A ; 6 cm) và (B ; 4 cm) cắt nhau tại hai điểm C và D với AB = 8 cm. Các đường tròn tâm A, B cắt đoạn thẳng AB lần lượt tại M, N.
Đề bài
Cho hai đường tròn (A ; 6 cm) và (B ; 4 cm) cắt nhau tại hai điểm C và D với AB = 8 cm. Các đường tròn tâm A, B cắt đoạn thẳng AB lần lượt tại M, N.
a) Tính AC, BD, AN, BM.
b) N có là trung điểm của đoạn thẳng AB không ?
c) M có là trung điểm của đoạn thẳng BN không ?
Lời giải chi tiết
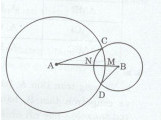
a)Hai điểm C, D nằm trên đường tròn (A; 6cm) nên AC = 6cm, AD = 6cm.
Hai điểm C, D nằm trên đường tròn (B; 4cm) nên BC = 4cm, BD = 4cm.
N nằm trên đường tròn (B; 4cm) nên NB = 4cm.
Trên tia BA có BN = 4cm, BA = 8cm vì 4cm < 8cm nên điểm N nằm giữa hai điểm B và A. Do đó: AN + NB = AB => AN = AB - NB = 8 - 4 = 4 (cm).
M nằm trên đường tròn (A; 6cm) nên AM = 6cm.
Trên tia AB có AM = 6cm, AB = 8cm vì 6cm < 8cm nên điểm M nằm giữa hai điểm A và B. Do đó: AM + MB = AB => MB = AB - AM = 8 - 6 = 2 (cm).
b) Ta có: N là trung điểm của đoạn thẳng AB vì N nằm giữa hai điểm A và B.
\(AN = NB = {{AB} \over 2} = (4cm)\)
c) Trên tia AB có AN = 4cm, AM = 6cm.
Vì AN < AM (4cm < 6cm) nên điểm N nằm giữa hai điểm A và M.
Ta có: AN + MN = AM => MN = AM - AN = 6 - 4 = 2(cm)
Do đó: \(MN = MB = {{NB} \over 2}( = 2cm).\)
Mà M nằm giữa N và B (cân a). Nên M là trung điểm của đoạn thẳng BN.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2 trang 116 Tài liệu dạy – học toán 6 tập 2 timdapan.com"