Bài 18 trang 21 SGK Toán 7 tập 2

Đề bài

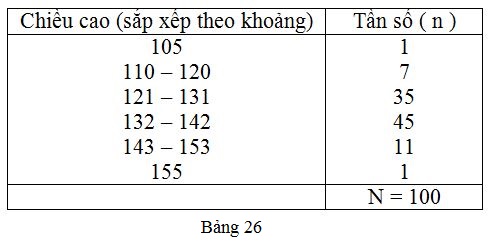
Đo chiều cao của \(100\) học sinh lớp \(6\) (đơn vị đo: cm) và được kết quả theo bảng \(26\):

a) Bảng này có gì khác so với những bảng "tần số" đã biết ?

b) Ước tính số trung bình cộng trong trường hợp này.

(Hướng dẫn: 

- Tính số trung bình cộng của từng khoảng. Số đó chính là trung bình cộng của giá trị lớn nhất và nhỏ nhất của khoảng. Ví dụ: trung bình cộng của khoảng 110 – 120 là 115.

- Nhân các số trung bình cộng vừa tìm được với các tần số tương ứng.

- Thực hiện tiếp các bước theo quy tắc đã học.) 

Lời giải chi tiết

a) Bảng này có khác so với bảng tần số đã học.

Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (\(10\) đơn vị) mà không tính riêng từng giá trị khác nhau.

b) Số trung bình cộng

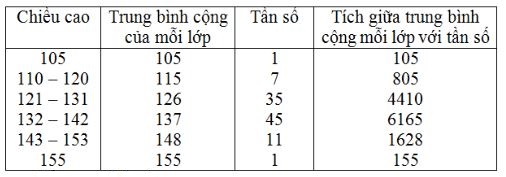
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.

Số trung bình cộng:

       \(\overline{X}=\dfrac{105+805+4410+6165+1628+155}{100}\)\(= 132,68 (cm).\) 

Chú ý: Số liệu ở cột trung bình cộng của mỗi lớp được tính như sau: Ta lấy tổng chiều cao đầu + chiều cao cuối của mỗi lớp, sau đó chia cho 2. Ví dụ: \(\dfrac{{110 + 120}}{2} = \dfrac{{230}}{2} = 115\)