Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao

Câu 16.

Một hình trụ có diện tích xung quanh bằng 4, diện tích đáy bằng diện tích một mặt cầu bán kính bằng 1. Thể tích khối trụ đó là

\(\eqalign{  & (A)\;4;  \cr  & (B)\;6;  \cr  & (C)\;8;  \cr  & (D)\;10. \cr} \)

Lời giải chi tiết:

Chọn (A).

Diện tích mặt cầu bán kính bằng \(1\) là \({S_c} = 4\pi {.1^2} = 4\pi \)

\( \Rightarrow {S_d} = {S_c}\) \( \Leftrightarrow \pi {R^2} = 4\pi  \Leftrightarrow R = 2\)

\(\begin{array}{l} \Rightarrow h = \frac{{{S_{xq}}}}{{2\pi R}} = \frac{4}{{2\pi .2}} = \frac{1}{\pi }\\ \Rightarrow V = \pi {R^2}h = \pi {.2^2}.\frac{1}{\pi } = 4\end{array}\)

Câu 17.

Một hình trụ có bán kính đáy bằng 1, thiết diện qua trục là hình vuông. Thể tích khối cầu ngoại tiếp hình trụ là

\(\eqalign{  & (A)\;6\pi \sqrt 3 ;  \cr  & (B)\;3\pi \sqrt 3 ;  \cr  & (C)\;{{4\pi \sqrt 2 } \over 3};  \cr  & (D)\;{{8\pi \sqrt 2 } \over 3}. \cr} \)

Lời giải chi tiết:

Chọn (D).

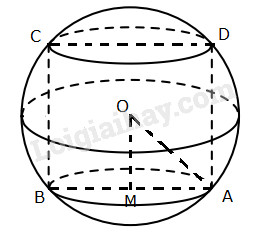
Ta có: \(OM = MA = 1\)

\( \Rightarrow OA = \sqrt {O{M^2} + M{A^2}} \) \( = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \)

\( \Rightarrow V = \frac{4}{3}\pi .O{A^3}\) \( = \frac{4}{3}\pi .{\left( {\sqrt 2 } \right)^3} = \frac{{8\pi \sqrt 2 }}{3}\)

Câu 18.

Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng \(4\pi \). Diện tích mặt cầu ngoại tiếp hình trụ là

\(\eqalign{  & (A)\;12\pi ;  \cr  & (B)\;10\pi ;  \cr  & (C)\;8\pi ;  \cr  & (D)\;6\pi . \cr} \)

Lời giải chi tiết:

Chọn (C ).

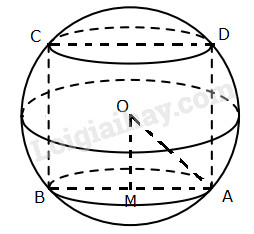
Ta có:

\(\begin{array}{l}AD = 2AM\\ \Rightarrow {S_{xq}} = 2\pi .AM.AD\\ \Leftrightarrow 4\pi  = 2\pi .AM.2AM\\ \Leftrightarrow AM = 1\end{array}\)

\(\begin{array}{l} \Rightarrow OA = \sqrt {O{M^2} + M{A^2}} \\ = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \\ \Rightarrow {S_c} = 4\pi .{\left( {\sqrt 2 } \right)^2} = 8\pi \end{array}\)

Câu 19.

Thể tích một khối trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng \(4\pi \) là

\(\eqalign{  & (A)\;\pi ;  \cr  & (B)\;2\pi ;  \cr  & (C)\;3\pi ;  \cr  & (D)\;4\pi . \cr} \)

Lời giải chi tiết:

Chọn (B).

\(\begin{array}{l}
h = 2R\\
\Rightarrow {S_{xq}} = 2\pi Rh\\
\Leftrightarrow 4\pi = 2\pi .R.2R\\
\Leftrightarrow R = 1 \Rightarrow h = 2\\
\Rightarrow V = \pi {R^2}h = \pi {.1^2}.2 = 2\pi
\end{array}\)

Câu 20.

Diện tích toàn phần của một hình trụ có diện tích xung quanh bằng \(4\pi \), thiết diện qua trục là hình vuông bằng

\(\eqalign{  & (A)\;12\pi ;  \cr  & (B)\;10\pi ;  \cr  & (C)\;8\pi ;  \cr  & (D)\;6\pi . \cr} \)

Lời giải chi tiết:

Chọn (D).

\(\begin{array}{l}
h = 2R\\
\Rightarrow {S_{xq}} = 2\pi Rh\\
\Leftrightarrow 4\pi = 2\pi .R.2R\\
\Leftrightarrow R = 1 
\end{array}\)

\(\begin{array}{l}
\Rightarrow {S_{tp}} = {S_{xq}} + 2\pi {R^2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\, = 4\pi + 2\pi {.1^2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\, = 6\pi
\end{array}\)

Câu 21.

Một hình trụ có diện tích xung quanh bằng \(4\pi \), thiết diện qua trục là hình vuông. Một mặt phẳng \(\left( \alpha  \right)\) song song với trục, cắt hình trụ theo thiết diện ABB’A’, biết một cạnh của thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 120⁰. Diện tích thiết diện ABB’A’ là

\(\eqalign{  & (A)\;\sqrt 3 ;  \cr  & (B)\;2\sqrt 3 ;  \cr  & (C)\;2\sqrt 2 ;  \cr  & (D)\;3\sqrt 2 . \cr} \)

Lời giải chi tiết:

Chọn (B).

\(\begin{array}{l}
h = 2R\\
\Rightarrow {S_{xq}} = 2\pi Rh\\
\Leftrightarrow 4\pi = 2\pi .R.2R\\
\Leftrightarrow R = 1 \Rightarrow h = 2 
\end{array}\)

\(\begin{array}{l}
A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos {120^0}\\
= {1^2} + {1^2} - 2.1.1.\left( { - \frac{1}{2}} \right) = 3\\
\Rightarrow AB = \sqrt 3 \\
\Rightarrow {S_{ABB'A'}} = AB.AA' = \sqrt 3 .2 = 2\sqrt 3
\end{array}\)

Câu 22.

Cho tứ diện đều ABCD cạnh bằng a. Diện tích xung quanh của hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện ABCD là

\(\eqalign{  & (A){{2\pi {a^2}\sqrt 2 } \over 3};  \cr  & (B){{\pi {a^2}\sqrt 2 } \over 3};  \cr  & (C)\pi {a^2}\sqrt 3 ;  \cr  & (D){{\pi {a^2}\sqrt 3 } \over 2}. \cr} \)

Lời giải chi tiết:

Chọn (A).

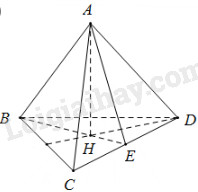
Bán kính đáy hình trụ:

\(R = HB = \frac{2}{3}BE\) \( = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)

Chiều cao hình trụ:

\(\begin{array}{l}h = AH = \sqrt {A{B^2} - B{H^2}} \\ = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}  = \frac{{a\sqrt 6 }}{3}\\ \Rightarrow {S_{xq}} = 2\pi Rh\\ = 2\pi .\frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt 6 }}{3} = \frac{{2\pi {a^2}\sqrt 2 }}{3}\end{array}\)

Câu 23.

Cho tứ diện đều ABCD cạnh a. Diện tích xung quanh của hình trụ có đáy là đường tròn nội tiếp tam giác BCD, chiều cao bằng chiều cao của tứ diện ABCD là

\(\eqalign{  & (A){{\pi {a^2}\sqrt 3 } \over 2};  \cr  & (B){{\pi {a^2}\sqrt 2 } \over 3};  \cr  & (C){{\pi {a^2}\sqrt 3 } \over 3};  \cr  & (D){{\pi {a^2}\sqrt 2 } \over 2}. \cr} \)

Lời giải chi tiết:

Chọn (B).

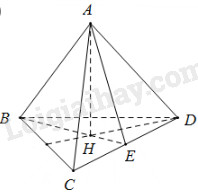
Bán kính đáy hình trụ:

\(R = HE = \frac{1}{3}BE\) \( = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\)

\(BH = \frac{2}{3}BE = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)

Chiều cao hình trụ:

\(\begin{array}{l}h = AH = \sqrt {A{B^2} - B{H^2}} \\ = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}  = \frac{{a\sqrt 6 }}{3}\end{array}\)

\( \Rightarrow {S_{xq}} = 2\pi Rh\) \( = 2\pi .\frac{{a\sqrt 3 }}{6}.\frac{{a\sqrt 6 }}{3} = \frac{{\pi {a^2}\sqrt 2 }}{3}\)

Câu 24.

Một hình trụ có bán kính bằng R và thiết diện qua trục là hình vuông. Thể tích của khối lăng trụ tứ giác đều nội tiếp hình trụ là

\(\eqalign{  & (A)\;2{R^3};  \cr  & (B)\;3{R^3};  \cr  & (C)\;4{R^3};  \cr  & (D)\;5{R^3}. \cr} \)

Lời giải chi tiết:

Chọn (C ).

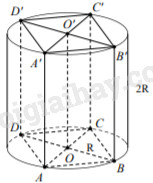
\(ABCD\) là hình vuông có \(AC = BD = 2R\)

\( \Rightarrow {S_{ABCD}} = \frac{1}{2}AC.BD\) \( = \frac{1}{2}.2R.2R = 2{R^2}\)

Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) là:

\(V = {S_{ABCD}}.AA' = 2{R^2}.2R = 4{R^3}\)

Câu 25.

Thiết diện qua trục của một hình nón là tam giác đều cạnh bằng 2. Một mặt cầu có diện tích bằng diện tích toàn phần của hình nón sẽ có bán kính là

\(\eqalign{  & (A)\;2\sqrt 3 ;  \cr  & (B)\;2;  \cr  & (C)\;\sqrt 3 ;  \cr  & (D)\;{{\sqrt 3 } \over 2}. \cr} \)

Lời giải chi tiết:

Chọn (D).

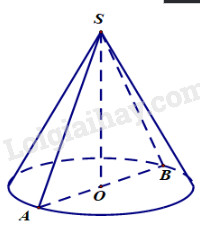
\(SAB\) đều cạnh \(2\) nên \(R = OA = 1,l = SA = 2\)

\(\begin{array}{l} \Rightarrow {S_{tp}} = \pi Rl + \pi {R^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \pi .1.2 + \pi {.1^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 3\pi \end{array}\)  

\(\begin{array}{l} \Rightarrow {S_c} = {S_{tp}} = 3\pi \\ \Leftrightarrow 4\pi {r^2} = 3\pi \\ \Leftrightarrow {r^2} = \frac{3}{4}\\ \Leftrightarrow r = \frac{{\sqrt 3 }}{2}\end{array}\)

Câu 26.

Một hình hộp chữ nhật có đáy là hình vuông cạnh a, cạnh bên của hình hộp bằng 2a. Thể tích của hình nón có đáy là đường tròn ngoại tiếp một đáy hình hộp và đỉnh là tâm của đáy còn lại của hình hộp là

\(\eqalign{  & (A)\;{{\pi {a^3}} \over 3};  \cr  & (B)\;{{\pi {a^3}} \over 2};  \cr  & (C)\;\pi {a^3};  \cr  & (D)\;2\pi {a^3}. \cr} \)

Lời giải chi tiết:

Chọn (A).

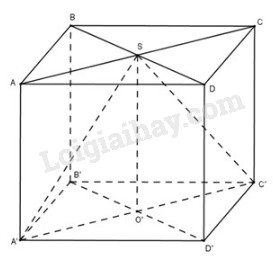
\(A'B'C'D'\) là hình vuông cạnh \(a\) nên \(R = O'A' = \frac{{a\sqrt 2 }}{2}\).

Thể tích \(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .O'A{'^2}.SO'\) \( = \frac{1}{3}\pi .{\left( {\frac{{a\sqrt 2 }}{2}} \right)^2}.2a = \frac{{\pi {a^3}}}{3}\)

Câu 27.

Một hình chữ nhật có đáy là hình vuông cạnh a, cạnh bên của hình hộp bằng 2a. Diện tích xung quanh của hình nón có đáy là đường tròn nội tiếp một đáy hình hộp và đỉnh là tâm của đáy còn lại của hình hộp là

\(\eqalign{  & (A)\;{{\pi {a^2}\sqrt {17} } \over 2};  \cr  & (B)\;{{\pi {a^2}\sqrt {17} } \over 4};  \cr  & (C)\;{{3\pi {a^2}} \over 2};  \cr  & (D)\;3\pi {a^2}. \cr} \)

Lời giải chi tiết:

Chọn (B).

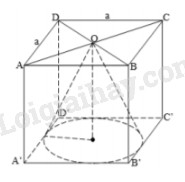
Bán kính \(r = \frac{a}{2}\).

Đường sinh \(l = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt {17} }}{2}\)

Diện tích xung quanh:

\({S_{xq}} = \pi rl\) \( = \pi .\frac{a}{2}.\frac{{a\sqrt {17} }}{2} = \frac{{\pi {a^2}\sqrt {17} }}{4}\)

Câu 28.

Một hình nón có thiết diện qua trục là tam giác đều. Tỉ số thể tích của  khối cầu ngoại tiếp và khối cầu nội tiếp khối nón là

\(\eqalign{  & (A)\;8;  \cr  & (B)\;6;  \cr  & (C)\;4;  \cr  & (D)\;2. \cr} \)

Lời giải chi tiết:

Chọn (A).

Thiết diện qua trục là tam giác đề (hình vẽ) nên \(\frac{R}{r} = 2\)

\( \Rightarrow \) thể tích khối cầu ngoại tiếp \({V_1} = \frac{4}{3}\pi {R^3}\)

Thể tích khối cầu nội tiếp \({V_2} = \frac{4}{3}\pi {r^3}\)

Tỉ số thể tích \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{4}{3}\pi {R^3}}}{{\frac{4}{3}\pi {r^3}}} = {\left( {\frac{R}{r}} \right)^3} = {2^3} = 8\)

Câu 29.

Cho tứ diện ABCD có \(DA \bot mp(ABC),\) \(DB \bot BC,AD = AB = BC = a.\) Kí hiệu \({V_1},{V_2},{V_3}\) lần lượt là thể tích của hình nón xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi quay quanh BC. Trong các mệnh đề sau, mệnh đề nào đúng ?

\(\eqalign{  & (A)\;{V_1} + {V_2} = {V_3};  \cr  & (B)\;{V_1} + {V_3} = {V_2};  \cr  & (C)\;{V_2} + {V_3} = {V_1};  \cr  & (D)\;{V_1} = {V_2} = {V_3}. \cr} \)

Lời giải chi tiết:

Chọn (A).

Câu 30.

Một hình nón có bán kính đáy bằng R, đường cao \({{4R} \over 3}\). Khi đó, góc ở đỉnh của hình nón là \(2\alpha \) mà

\(\eqalign{  & (A)\sin \alpha  = {3 \over 5};  \cr  & (B)\cos \alpha  = {3 \over 5};  \cr  & (C)\tan \alpha  = {3 \over 5};  \cr  & (D)\cot \alpha  = {3 \over 5}. \cr} \)

Lời giải chi tiết:

Chọn (A).

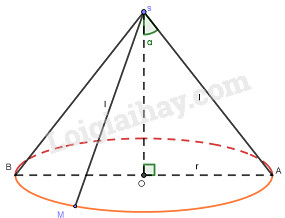
\(\begin{array}{l}
OA = R,SO = \frac{{4R}}{3}\\
\Rightarrow SA = \sqrt {O{A^2} + S{O^2}} \\
= \sqrt {{R^2} + {{\left( {\frac{{4R}}{3}} \right)}^2}} = \frac{{5R}}{3}\\
\Rightarrow \sin \alpha = \frac{{OA}}{{SA}} = \frac{R}{{\frac{{5R}}{3}}} = \frac{3}{5}
\end{array}\)