Bài 1: Dao động điều hòa

Video bài giảng

1. Dao động cơ, dao động tuần hoàn

Dao động cơ là chuyển động qua lại của vật quanh vị trí cân bằng.
Dao động tuần hoàn là dao động mà sau những khoảng thời gian bằng nhau, gọi là chu kì, vật trở lại vị trí cũ theo hướng cũ. Dao động tuần hoàn đơn giản nhất là dao động điều hòa.

2. Dao động điều hòa

a. Ví dụ dao động điều hòa

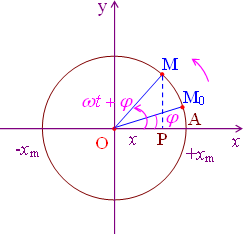
Giả sử M chuyển động theo chiều dương vận tốc góc là \(\omega, P\) là hình chiếu của M lên Ox.
- Tại t = 0, M có tọa độ góc \(\varphi\)
- Sau thời gian t, M có tọa độ góc \(\varphi+\omega t\)
- Khi đó: \(\overline{OP}\) = \(x\); \(x=OMcos(\omega t+\varphi)\)
- Đặt A = OM ta có: \(x=Acos(\omega t+\varphi)\)
Trong đó \(A, \omega, \varphi\) là hằng số
Do hàm cosin là hàm điều hòa nên điểm P được gọi là dao động điều hòa.

b. Định nghĩa dao động điều hòa

Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.

c. Phương trình

Phương trình \(x = Acos(\omega t + \varphi)\) gọi là phương trình của dao động điều hòa.
- A là biên độ dao động, là li độ cực đại của vật, A > 0.
- \(\omega t + \varphi\) là pha của dao động tại thời điểm t
- \(\varphi\) là pha ban đầu tại t = 0 (\(\varphi\) < 0, \(\varphi\)>0, \(\varphi\) = 0)

d. Chú ý

Điểm P dao động điều hòa trên một đoạn thẳng luôn luôn có thể coi là hình chiếu của điểm M chuyển động tròn đều lên đường kính là đoạn thẳng đó.
Ta quy ước chọn trục x làm gốc để tính pha của dao động và chiều tăng của pha tương ứng với chiều tăng của góc \(\widehat{MOP}\) trong chuyển động tròn đều.

3. Chu kì, tần số, tần số góc của dao động điều hòa

a. Chu kì và tần số

Khi vật trở về vị trí cũ hướng cũ thì ta nói vật thực hiện 1 dao động toàn phần.
- Chu kì (T): của dao động điều hòa là khoảng thời gian để vật thực hiện một dao động toàn phần. Đơn vị là s
- Tần số (f): của dao động điều hòa là số dao động tuần hoàn thực hiện trong một s. Đơn vị là 1/s hoặc Hz.

b. Tần số góc

Trong dao động điều hòa \(\omega\) được gọi là tần số góc.
Giữa tần số góc, chu kì và tần số có mối liên hệ: \(\omega = \frac{2\pi}{T}=2\pi f\)

4. Vận tốc và gia tốc của dao động điều hòa

a. Vận tốc

Vận tốc là đạo hàm của li độ theo thời gian.

\(v=x'= - \omega Asin (\omega t+\varphi)\)

Vận tốc cũng biến thiên theo thời gian.
- Tại \(x=\pm A\) thì \(v = 0\)
- Tại \(x = 0\) thì \(v = v_{max} = \omega A\)

b. Gia tốc

Gia tốc là đạo hàm của vận tốc theo thời gian

\(a=v'=x{}''= - \omega^2 Acos (\omega t+\varphi)\)

\(a= - \omega^2 x\)

Tại \(x=0\) thì \(a = 0\)
Tại \(x=\pm A\) thì \(a=a_{max}=\omega^2A\)

5. Đồ thị của dao động điều hòa

Đồ thị của dao động điều hòa với \(\varphi= 0\) có dạng hình sin nên người ta còn gọi là dao động hình sin.

Bài 1

Một vật dao động điều hòa trên đoạn thẳng dài 4cm với \(f = 10Hz\). Lúc \(t = 0\) vật qua VTCB theo chiều dương của quỹ đạo. Viết phương trình dao động của vật.

Hướng dẫn giải

Ta có tần số góc \(\omega = 2\pi f = \pi\) và biên độ \(A = \frac{MN}{2} = 2cm\)

Điều kiện ban đầu \(t = 0\): \(x_0 = 0, v_0 > 0\Rightarrow\) \(\varphi =-\frac{\pi}{2}\Rightarrow x=2cos(20\pi t-\frac{\pi}{2})\) (cm).

Bài 2

Phương trình của một vật dao động điều hòa có dạng: \(x=-6cos(\pi t+\frac{\pi}{6})\) (cm). Hãy cho biết chu kì, biên độ và pha ban đầu của dao động.

Hướng dẫn giải

Từ phương trình dao động ta có:

\(x=-6cos(\pi t+\frac{\pi}{6})\) = \(x= 6cos(\pi t+\frac{\pi}{6}-\pi)\) (cm)

\(\Rightarrow A=6\) (cm) ; \(\omega= 2 \pi\) (rad/s) ; \(\varphi= - \frac{5 \pi}{6}\) (rad)

Bài 3:

Một vật chuyển động điều hòa phải mất 0,25 s để đi từ điểm có vận tốc bằng 0 tới điểm tiếp theo cũng có vận tốc bằng 0. Khoảng cách giữa hai điểm là 36 cm. Tính chu kì, tần số và biên độ của dao động.

Hướng dẫn giải

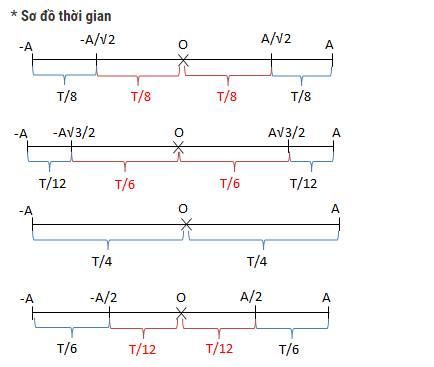
Sử dụng sơ đồ thời gian để tìm ra thời gian đi từ vị trí này đến vị trí tiếp theo của vật

Sơ đồ thời gian

a. \(T = 0,5 s. \)

b. \(f = 2 Hz; A = 18 cm.\)

Hai vị trí biên cách nhau 36 cm, nên biên độ A = 18 cm.
Thời gian đi từ vị trí nầy đến vị trí bên kia là \(\frac{1}{2}T\) nên chu kì \(T = 0,5 s. \) và tần số \(f = \frac{1}{T} = 2Hz\)

1. Dao động cơ, dao động tuần hoàn

Dao động cơ là chuyển động qua lại của vật quanh vị trí cân bằng.
Dao động tuần hoàn là dao động mà sau những khoảng thời gian bằng nhau, gọi là chu kì, vật trở lại vị trí cũ theo hướng cũ. Dao động tuần hoàn đơn giản nhất là dao động điều hòa.

2. Dao động điều hòa

a. Ví dụ dao động điều hòa

Giả sử M chuyển động theo chiều dương vận tốc góc là \(\omega, P\) là hình chiếu của M lên Ox.
- Tại t = 0, M có tọa độ góc \(\varphi\)
- Sau thời gian t, M có tọa độ góc \(\varphi+\omega t\)
- Khi đó: \(\overline{OP}\) = \(x\); \(x=OMcos(\omega t+\varphi)\)
- Đặt A = OM ta có: \(x=Acos(\omega t+\varphi)\)
Trong đó \(A, \omega, \varphi\) là hằng số
Do hàm cosin là hàm điều hòa nên điểm P được gọi là dao động điều hòa.

b. Định nghĩa dao động điều hòa

Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.

c. Phương trình

Phương trình \(x = Acos(\omega t + \varphi)\) gọi là phương trình của dao động điều hòa.
- A là biên độ dao động, là li độ cực đại của vật, A > 0.
- \(\omega t + \varphi\) là pha của dao động tại thời điểm t
- \(\varphi\) là pha ban đầu tại t = 0 (\(\varphi\) < 0, \(\varphi\)>0, \(\varphi\) = 0)

d. Chú ý

Điểm P dao động điều hòa trên một đoạn thẳng luôn luôn có thể coi là hình chiếu của điểm M chuyển động tròn đều lên đường kính là đoạn thẳng đó.
Ta quy ước chọn trục x làm gốc để tính pha của dao động và chiều tăng của pha tương ứng với chiều tăng của góc \(\widehat{MOP}\) trong chuyển động tròn đều.

3. Chu kì, tần số, tần số góc của dao động điều hòa

a. Chu kì và tần số

Khi vật trở về vị trí cũ hướng cũ thì ta nói vật thực hiện 1 dao động toàn phần.
- Chu kì (T): của dao động điều hòa là khoảng thời gian để vật thực hiện một dao động toàn phần. Đơn vị là s
- Tần số (f): của dao động điều hòa là số dao động tuần hoàn thực hiện trong một s. Đơn vị là 1/s hoặc Hz.

b. Tần số góc

Trong dao động điều hòa \(\omega\) được gọi là tần số góc.
Giữa tần số góc, chu kì và tần số có mối liên hệ: \(\omega = \frac{2\pi}{T}=2\pi f\)

4. Vận tốc và gia tốc của dao động điều hòa

a. Vận tốc

Vận tốc là đạo hàm của li độ theo thời gian.

\(v=x'= - \omega Asin (\omega t+\varphi)\)

Vận tốc cũng biến thiên theo thời gian.
- Tại \(x=\pm A\) thì \(v = 0\)
- Tại \(x = 0\) thì \(v = v_{max} = \omega A\)

b. Gia tốc

Gia tốc là đạo hàm của vận tốc theo thời gian

\(a=v'=x{}''= - \omega^2 Acos (\omega t+\varphi)\)

\(a= - \omega^2 x\)

Tại \(x=0\) thì \(a = 0\)
Tại \(x=\pm A\) thì \(a=a_{max}=\omega^2A\)

5. Đồ thị của dao động điều hòa

Đồ thị của dao động điều hòa với \(\varphi= 0\) có dạng hình sin nên người ta còn gọi là dao động hình sin.

Bài 1

Hướng dẫn giải

Ta có tần số góc \(\omega = 2\pi f = \pi\) và biên độ \(A = \frac{MN}{2} = 2cm\)

Điều kiện ban đầu \(t = 0\): \(x_0 = 0, v_0 > 0\Rightarrow\) \(\varphi =-\frac{\pi}{2}\Rightarrow x=2cos(20\pi t-\frac{\pi}{2})\) (cm).

Bài 2

Phương trình của một vật dao động điều hòa có dạng: \(x=-6cos(\pi t+\frac{\pi}{6})\) (cm). Hãy cho biết chu kì, biên độ và pha ban đầu của dao động.

Hướng dẫn giải

Từ phương trình dao động ta có:

\(x=-6cos(\pi t+\frac{\pi}{6})\) = \(x= 6cos(\pi t+\frac{\pi}{6}-\pi)\) (cm)

\(\Rightarrow A=6\) (cm) ; \(\omega= 2 \pi\) (rad/s) ; \(\varphi= - \frac{5 \pi}{6}\) (rad)

Bài 3:

Hướng dẫn giải

Sử dụng sơ đồ thời gian để tìm ra thời gian đi từ vị trí này đến vị trí tiếp theo của vật

Sơ đồ thời gian

a. \(T = 0,5 s. \)

b. \(f = 2 Hz; A = 18 cm.\)

Hai vị trí biên cách nhau 36 cm, nên biên độ A = 18 cm.
Thời gian đi từ vị trí nầy đến vị trí bên kia là \(\frac{1}{2}T\) nên chu kì \(T = 0,5 s. \) và tần số \(f = \frac{1}{T} = 2Hz\)