Bài 36 trang 60 SGK Đại số 10 nâng cao

Vẽ đồ thị của mỗi hàm số sau:

LG a

\(y = \left\{ \matrix{
- x + 1\,\,\,\,\,\,\,\,;x \le - 1 \hfill \cr 
- {x^2} + 3\,\,\,\,\,;x > - 1 \hfill \cr} \right.\)

Lời giải chi tiết:

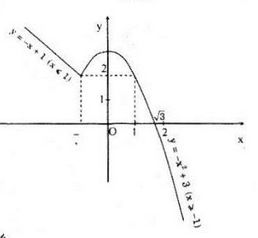
* Vẽ đường thẳng y = -x + 1 qua A(1, 0) và B(-1, 2)

* Vẽ parabol y = -x² + 3 có:

+ Đỉnh I(0, 3)

+ Trục đối xứng Oy

+ Đi qua điểm (1;2), cắt Oy tại (0;3)

Đồ thị cần vẽ gồm hai phần:

+ Phần đường thẳng ứng với \(x\le -1\), tức là để lại phần này và xóa phần đường thẳng ứng với x > -1 đi.

+ Phần parabol ứng với x > -1, tức là để lại phần này và xóa phần ứng với \(x\le -1\) đi.

Đồ thị:

LG b

\(y = \left\{ \matrix{
{1 \over 2}{(x + 3)^2}\,\,\,\,\,\,\,\,\,\,\,;x \le - 1 \hfill \cr 
2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x > - 1 \hfill \cr} \right.\)

Lời giải chi tiết:

Ta có: 

\(y = \left\{ \begin{array}{l}
\frac{1}{2}{x^2} + 3x + \frac{9}{2}\,voi\,x \le - 1\\
2\,voi\,x > - 1
\end{array} \right.\)

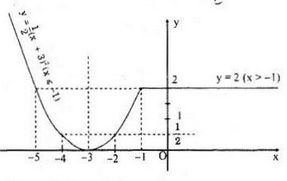
* Vẽ parabol \(y = \frac{1}{2}{x^2} + 3x + \frac{9}{2}\)

+ Đỉnh (-3;0)

+ Trục đối xứng x=-3.

+ Đi qua điểm (-1;2), (-5;2).

* Vẽ đường thẳng y=2 (song song với trục Ox và đi qua điểm (0;2)

Phần đồ thị cần tìm là hợp của hai phần sau:

+ parabol \(y = \frac{1}{2}{x^2} + 3x + \frac{9}{2}\) ứng với \(x\le -1\)

+ Nừa đường thẳng y=2 ứng với x > -1.

Đồ thị hàm số: