Bài 35 trang 60 SGK Đại số 10 nâng cao

Vẽ đồ thị và lập bảng biến thiên của các hàm số sau:

LG a

\(y = \,|{x^2} + \sqrt 2 x|\)

Phương pháp giải:

Đồ thị hàm số y=|f(x)| có được từ đồ thị hàm số y=f(x) như sau:

+) Giữ nguyên phần đồ thị phía trên trục Ox.

+) Lấy đối xứng phần dưới qua Ox và xóa phần dưới cũ đi.

Lời giải chi tiết:

Vẽ đồ thị hàm số \(y = \,{x^2} + \sqrt 2 x\)  (P₁) rồi suy ra đồ thị hàm số: \(y = \,|{x^2} + \sqrt 2 x|\)  (P)

Hoành độ của đỉnh: \({x_0} =  - {b \over {2a}} = {{ - \sqrt 2 } \over 2}\)\( \Rightarrow {y_0}  = {\left( { - \frac{{\sqrt 2 }}{2}} \right)^2} + \sqrt 2 .\left( { - \frac{{\sqrt 2 }}{2}} \right)\)\(= {1 \over 2} - 1 =  - {1 \over 2}\)

Đỉnh \(I( - {{\sqrt 2 } \over 2}; - {1 \over 2})\)

Bảng giá trị:

Đồ thị hàm số:

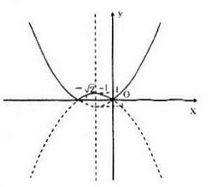
Ta giữ nguyên phần đồ thị trên trục hoành và lấy đối xứng phần đồ thị của hàm số  \(y = \,{x^2} + \sqrt 2 x\) phía dưới trục hoành qua Ox ta được đồ thị của hàm \(y = \,|{x^2} + \sqrt 2 x|\) ( đồ thị là phần nét liền trên hình vẽ)

Bảng biến thiên:

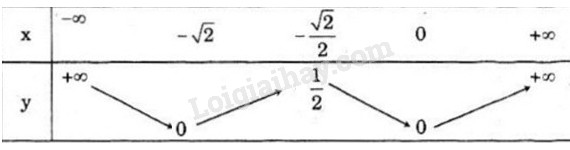
LG b

y = -x² + 2|x| + 3

Lời giải chi tiết:

Vẽ đồ thị hàm số y = -x² + 2x + 3 (P₁) rồi suy ra đồ thị hàm số: y = -x² + 2|x| + 3 (P)

Hoành độ đỉnh: \({x_0} =  - {b \over {2a}} = {{ - 2} \over { - 2}} = 1 \Rightarrow {y_0} = 4\)

Đỉnh I (1, 4)

Bảng giá trị:

Đồ thị hàm số:

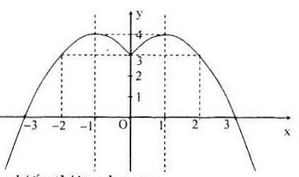
Bảng biến thiên

LG c

y = 0,5x² - |x – 1| + 1

Lời giải chi tiết:

y = 0,5x² - |x – 1| + 1

Ta có:

\(y = \left\{ \matrix{
0,5{x^2} - x + 2\,\,\,\,\,\,\,;x \ge 1 \hfill \cr 
0,5{x^2} + x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x < 1 \hfill \cr} \right.\)

Đồ thị hàm số:

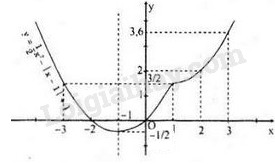
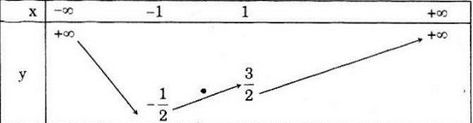
Bảng biến thiên: