Toán lớp 4 trang 17 - Bài 42: Tính chất phân phối của phép nhân đối với phép cộng - SGK Kết nối tri thức
Tính giá trị của các biểu thức sau với m = 4, n = 5, p = 3.Khối lớp Bốn có 2 lớp học vẽ, khối lớp Ba có 3 lớp học vẽ, mỗi lớp học vẽ có 12 bạn
Câu 1
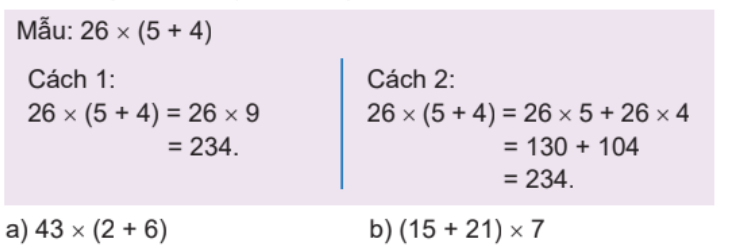
Tính bằng hai cách (theo mẫu).
Phương pháp giải:
a) Khi nhân một số với một tổng ta có thể nhân số đó với từng số hạng của tổng rồi cộng các kết quả với nhau.
a x (b + c) = a x b + a x c
b) Khi nhân một tổng với một số, ta có thể nhân từng số hạng của tổng với số đó rồi cộng các kết quả với nhau.
(a + b) x c = a x c + b x c
Lời giải chi tiết:
a) 43 x (2 + 6)
Cách 1: 43 x (2 + 6) = 43 x 8 = 344
Cách 2: 43 x (2 + 6) = 43 x 2 + 43 x 6 = 86 + 258 = 344
b) (15 + 21) x 7
Cách 1: (15 + 21) x 7 = 36 x 7 = 252
Cách 2: (15 + 21) x 7 = 15 x 7 + 21 x 7 = 105 + 147 = 252
Câu 2
a) Tính giá trị của các biểu thức sau với m = 4, n = 5, p = 3.
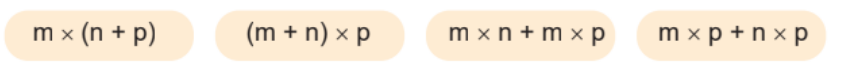
b) Hai biểu thức nào ở câu a có giá trị bằng nhau?
Phương pháp giải:
Thay chữ bằng số rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
a) Với m = 4, n = 5, p = 3 thì:
m x (n + p) = 4 x (5 + 3) = 4 x 8 = 32
(m + n) x p = (4 +5) x 3 = 9 x 3 = 27
m x n + m x p = 4 x 5 + 4 x 3 = 20 + 12 = 32
m x p + n x p = 4 x 3 + 5 x 3 = 12 + 15 = 27
b) Hai biểu thức có giá trị bằng nhau là:
m x (n + p) = m x n + m x p
(m + n) x p = m x p + n x p
Câu 3
Khối lớp Bốn có 2 lớp học vẽ, khối lớp Ba có 3 lớp học vẽ, mỗi lớp học vẽ có 12 bạn. Hỏi cả hai khối lớp có bao nhiêu bạn học vẽ?
Phương pháp giải:
Cách 1:
Bước 1: Số lớp học vẽ ở cả hai khối
Bước 2: Số bạn học vẽ = số bạn học vẽ ở mỗi lớp x số lớp học vẽ ở cả hai khối
Cách 2:
Bước 1: Tìm số bạn học vẽ ở khối lớp Bốn
Bước 2: Tìm số bạn học vẽ ở khối lớp Ba
Bước 3: Tìm số bạn học vẽ ở cả hai khối lớp
Lời giải chi tiết:
Tóm tắt:
Khối Bốn: 2 lớp
Khối Ba: 3 lớp
1 lớp: 12 bạn
Tất cả: ... ? bạn
Bài giải
Cách 1:
Số lớp học vẽ ở cả hai khối lớp là:
2 + 3 = 5 (lớp)
Số bạn học vẽ ở cả hai khối lớp là:
12 x 5 = 60 (bạn)
Đáp số: 60 bạn
Cách 2:
Số bạn học vẽ ở khối lớp Bốn là:
12 x 2 = 24 (bạn)
Số bạn học vẽ ở khối lớp Ba là:
12 x 3 = 36 (bạn)
Số bạn học vẽ ở cả hai khối lớp là:
24 + 36 = 60 (bạn)
Đáp số: 60 bạn
Câu 1
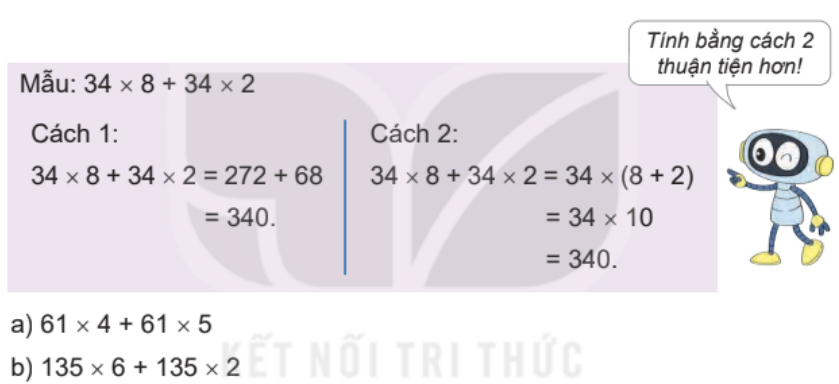
Tính bằng hai cách (theo mẫu):
Phương pháp giải:
Cách 1: Thực hiện phép nhân trước, phép cộng sau
Cách 2: Áp dụng các công thức:
a x b + a x c = a x (b + c)
Lời giải chi tiết:
a)
Cách 1: 61 x 4 + 61 x 5 = 244 + 305 = 549
Cách 2: 61 x 4 + 61 x 5 = 61 x (4 + 5) = 61 x 9 = 549
b)
Cách 1: 135 x 6 + 135 x 2 = 810 + 270 = 1 080
Cách 2: 135 x 6 + 135 x 2 = 135 x (6 + 2) = 1 080
Câu 2
Tính bằng cách thuận tiện.
a) 67 x 3 + 67 x 7
b) 45 x 6 + 45 x 4
c) 27 x 6 + 73 x 6
Phương pháp giải:
Áp dụng công thức:
a x b + a x c = a x (b + c
Lời giải chi tiết:
a) 67 x 3 + 67 x 7 = 67 x (3 + 7)
= 67 x 10 = 670
b) 45 x 6 + 45 x 4 = 45 x (6 + 4)
= 45 x 10 = 450
c) 27 x 6 + 73 x 6 = 6 x (27 + 73)
= 6 x 100 = 600
Câu 3
Tính (theo mẫu).
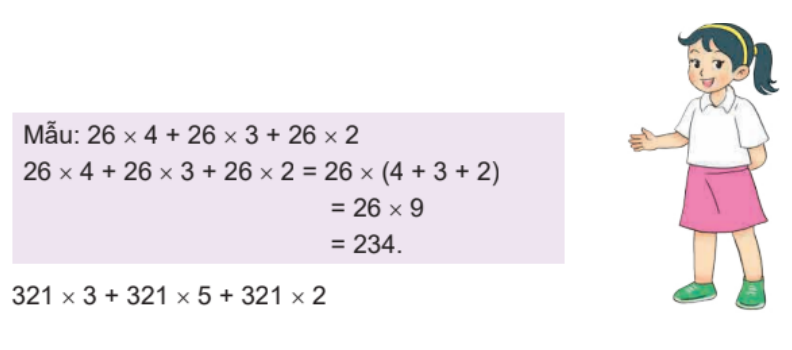
Phương pháp giải:
Áp dụng công thức:
a x b + a x c + a x d = a x (b + c + d)
Lời giải chi tiết:
321 x 3 + 321 x 5 + 321 x 2 = 321 x (3 + 5 + 2)
= 321 x 10
= 3 210
Câu 4
Người ta chuyển hàng để giúp đỡ đồng bào vùng lũ lụt. Đợt một chuyển được 3 chuyến, mỗi chuyến có 44 thùng hàng. Đợt hai chuyển được 3 chuyến, mỗi chuyến có 56 thùng hàng. Hỏi cả hai đợt đã chuyển được bao nhiêu thùng hàng?
Phương pháp giải:
Cách 1:
Bước 1: Tìm số thùng hàng chuyển đi trong đợt 1
Bước 2: Tìm số thùng hàng chuyển đi trong đợt 2
Bước 3: Tìm số thùng hàng chuyển đi trong cả hai đợt
Cách 2:
Bước 1: Tìm tổng số thùng đã chuyển đi mỗi chuyến ở cả hai đợt
Bước 2: Số thùng hàng chuyển đi trong cả hai đợt = Số thùng hàng ở mỗi chuyến x số chuyến
Lời giải chi tiết:
Tóm tắt:
Đợt 1: 3 chuyến
Mỗi chuyến: 44 thùng hàng
Đợt 2: 3 chuyến
Mỗi chuyến: 56 thùng hàng
Cả hai đợt: ? thùng hàng
Bài giải
Cách 1:
Số thùng hàng chuyển đi trong đợt 1 là:
44 x 3 = 132 (thùng hàng)
Số thùng hàng chuyển đi trong đợt 2 là:
56 x 3 = 168 (thùng hàng)
Số thùng hàng chuyển đi trong cả hai đợt là:
132 + 168 = 300 (thùng hàng)
Đáp số: 300 thùng hàng
Cách 2:
Số thùng hàng chuyển đi trong mỗi chuyến ở 2 đợt là:
44 + 56 = 100 (thùng hàng)
Số thùng hàng chuyển đi trong cả 2 đợt là:
100 x 3 = 300 (thùng hàng)
Đáp số: 300 thùng hàng.
Câu 1
Tính rồi so sánh giá trị của hai biểu thức (theo mẫu).
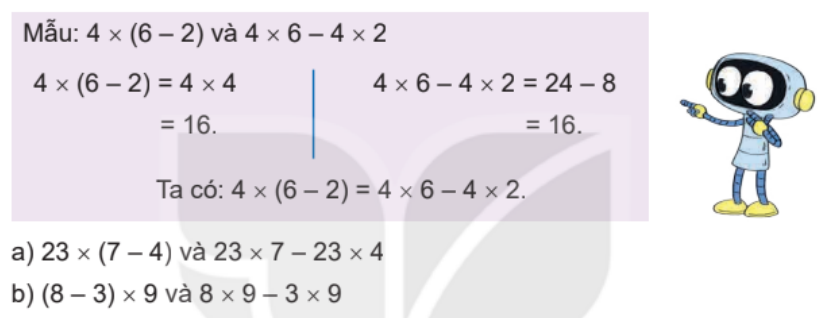
Phương pháp giải:
Tính giá trị của hai biểu thức rồi so sánh
Lời giải chi tiết:
a) 23 x (7 – 4) = 23 x 3
= 69
23 x 7 – 23 x 4 = 161 – 92
= 69
Ta có: 23 x (7 – 4) = 23 x 7 – 23 x 4
b) (8 – 3) x 9 = 5 x 9
= 45
8 x 9 – 3 x 9 = 72 – 27
= 45
Ta có: (8 – 3) x 9 = 8 x 9 – 3 x 9
Câu 2
a) Tính giá trị của biểu thức (theo mẫu)

b) >, <, =?
a x (b - c) ....... a x b - a x c
Phương pháp giải:
a) Thay chữ bằng số rồi tính giá trị của biểu thức.
b) Dựa vào kết quả của câu a để điền dấu thích hợp
Lời giải chi tiết:
a)

b) a x (b – c) = a x b – b x c
Câu 3
Tính bằng cách thuận tiện.
a) 48 x 9 – 48 x 8
b) 156 x 7 – 156 x 2
Phương pháp giải:
Áp dụng công thức: a x (b – c) = a x b – a x c
Lời giải chi tiết:
a) 48 x 9 – 48 x 8 = 48 x (9 – 8)
= 48 x 1
= 48
b) 156 x 7 – 156 x 2 = 156 x (7 – 2)
= 156 x 5
= 780
Câu 4
Một cửa hàng có 9 tấm vải hoa, mỗi tấm dài 36 m. Cửa hàng đã bán được 5 tấm vải hoa như vậy. Hỏi cửa hàng còn lại bao nhiêu mét vải hoa?
Phương pháp giải:
Cách 1:
Bước 1: Số tấm vải hoa còn lại = số tấm vải hoa có – số tấm vải hoa đã bán.
Bước 2: Số m vải hoa còn lại = độ dài mỗi tấm vải x số tấm vải hoa còn lại.
Cách 2:
Bước 1: Tìm số m vải hoa cửa hàng có
Bước 2: Tìm số m vải hoa cửa hàng đã bán
Bước 3: Số m vải hoa cửa hàng còn lại = số mét vải cửa hàng có – số mét vải cửa hàng đã bán.
Lời giải chi tiết:
Tóm tắt:
Có: 9 tấm vải
Mỗi tấm: 36 m
Đã bán: 5 tấm vải
Còn lại: ... ? m vải
Bài giải
Cách 1:
Số tấm vải hoa còn lại là:
9 – 5 = 4 (tấm)
Cửa hàng còn lại số mét vải hoa là:
36 x 4 = 144 (m)
Đáp số: 144 m vải hoa
Cách 2:
Số mét vải hoa cửa hàng có là:
36 x 9 = 324 (m)
Số mét vải hoa cửa hàng đã bán là:
36 x 5 = 180 (m)
Số mét vải hoa cửa hàng còn lại là:
324 – 180 = 144 (m)
Đáp số: 144 m vải hoa
Lý thuyết
Search google: "từ khóa + timdapan.com" Ví dụ: "Toán lớp 4 trang 17 - Bài 42: Tính chất phân phối của phép nhân đối với phép cộng - SGK Kết nối tri thức timdapan.com"







