Phương pháp giải bài tập hợp lực song song cùng chiều, ngược chiều – ngẫu lực
Tổng hợp phương pháp giải bài tập hợp lực song song cùng chiều, ngược chiều – ngẫu lực hay, chi tiết
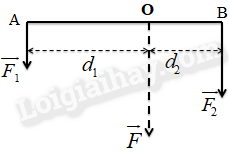
1. Quy tắc hợp lực song song cùng chiều
\(F = {F_1} + {F_2}\)
\({F_{ 1}}{d_1} = {F_2}{d_2}\)
Trong đó:
\(F\): là độ lớn hợp lực (N)
\({F_1},{F_2}\): là các thành phần lực song song cùng chiều (N)
\({d_1},{d_2}\): lần lượt là cánh tay đòn của lực \({F_1},{F_2}\) (m)
2. Momen của ngẫu lực
Đối với các trục quay vuông góc với mặt phẳng chứa ngẫu lực thì momen của ngẫu lực không phụ thuộc vào vị trí trục quay và luôn có giá trị:
\(M = F.d\)
Trong đó:
\(F\): là độ lớn của các lực tác dụng (N)
\(d\): là cánh tay đòn của ngẫu lực (m)
\(M\): là momen của ngẫu lực (N.m)
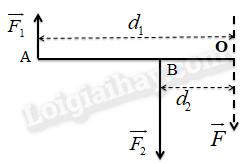
3. Quy tắc hợp lực song song ngược chiều
\(\begin{array}{l}F = \left| {{F_1} - {F_2}} \right|\\{F_1}{d_1} = {F_2}{d_2}\end{array}\)
Trong đó:
\(F\): là độ lớn hợp lực (N)
\({F_1},{F_2}\): là các thành phần lực song song ngược chiều (N)
\({d_1},{d_2}\): lần lượt là cánh tay đòn của lực \({F_1},{F_2}\) (m)
Bài tập ví dụ:
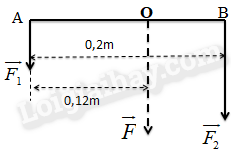
Bài 1: Hai lực song song cùng chiều, một lực có độ lớn 13 N cách lực kia 0,2m và cách giá của hợp lực 0,12m. Tính độ lớn của lực còn lại và hợp lức.
Hướng dẫn giải
Ta có:
\({d_1} = 0,12 \Rightarrow {d_2} = 0,2 - 0,12 = 0,08m\)
\({F_1}{d_1} = {F_2}{d_2} \Leftrightarrow 13.0,12 = {F_2}.0,08 \Leftrightarrow {F_2} = 19,5N\)
Hợp lực: \(F = {F_1} + {F_2} = 13 + 19,5 = 32,5N\)
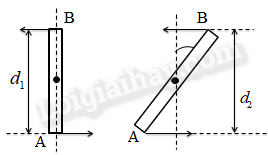
Bài 2: Thanh rắn mỏng, phẳng, đồng chất, trục quay đi qua trọng tâm của thanh. Tác dụng vào hai điểm A,B của thanh rắn cách nhau 4,5cm, ngẫu lực có độ lớn 5N. Tính momen ngẫu lực trong các trường hợp sau:
a) Thanh rắn đang ở vị trí thẳng đứng.
b) Thanh rắn đang ở vị trí hợp với phương thẳng đứng góc 300.
Hướng dẫn giải
a)
Ta có: \({d_1} = AB = 4,5cm\)
Suy ra: \(M = F.{d_1} = 5.4,{5.10^{ - 2}} = 0,225N.m\)
b)
Ta có: \({d_2} = AB.\cos {30^0} = 4,5.\frac{{\sqrt 3 }}{2} = \frac{{9\sqrt 3 }}{4}cm\)
Suy ra: \(M = F.{d_2} = 5.\frac{{9\sqrt 3 }}{4}{.10^{ - 2}} = 0,195N.m\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Phương pháp giải bài tập hợp lực song song cùng chiều, ngược chiều – ngẫu lực timdapan.com"