Lý thuyết về diện tích hình thang

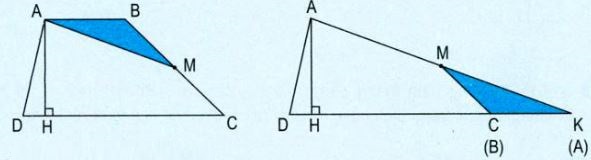
Cho hình thang ABCD và điểm M là trung điểm của cạnh BC. Cắt hình tam giác ABM rồi ghép với hình tứ giác AMCD (như hình vẽ) ta được hình tam giác ADK.

Dựa vào hình vẽ ta có:

Diện tích hình thang ABCD bằng diện tích hình tam giác ADK.

Diện tích hình tam giác ADK là \({S_{A{\rm{D}}K}} = \displaystyle{{DK \times AH} \over 2}\)

Mà \(\dfrac{HK \times AH}{2} = \dfrac{(DC+CK)\times AH}{2} \) \(=\dfrac{(DC+AB)\times AH}{2} \)

Vậy diện tích hình thang ABCD là \(\displaystyle {{\left( {DC + AB} \right) \times AH} \over 2}\).

Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.

                 \(S = \displaystyle {{\left( {a + b} \right) \times h} \over 2}\)

(\(S\) là diện tích; \(a,\,b\) là độ dài các cạnh đáy; \(h\) là chiều cao)