Lý thuyết ôn tập chương 3

I. Hình thoi

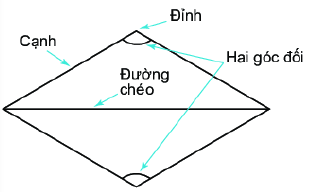
Hình thoi ABCD có:

- Bốn đỉnh A, B, C, D.

- Bốn cạnh bằng nhau:

- Hai cạnh đối AB và CD, AD và BC song song với nhau.

- Hai đường chéo AC và BD vuông góc với nhau.

Chu vi hình thoi cạnh a bằng độ dài cạnh nhân với bốn: \(C = 4a\)

Diện tích hình thoi cạnh a bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\)

II. Hình vuông

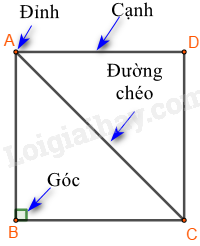
Bốn cạnh bằng nhau:  \(AB = BC = CD = DA; \)

Hai cạnh đối  \(AB \) và  \(CD; \)  \(AD \) và  \(BC \) song song với nhau;

Hai đường chéo bằng nhau:  \(AC = BD; \)

Bốn góc ở các đỉnh  \(A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D \) là góc vuông.

Chu vi hình vuông cạnh a là: \(C = 4a\)

Diện tích hình vuông cạnh a là: \(S = a.a = {a^2}\).

III. Hình bình hành

Hình bình hành ABCD có:

- Bốn đỉnh A, B, C, D.

- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,BC = AD\).

- Hai cặp cạnh đối diện song song: \(AB\) song song với \(CD\); \(BC\) song song với \(AD\).

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.

Chu vi hình bình hành : \(C = 2(a + b)\).

Diện tích hình bình hành là: \(S = b.h\)

Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.

IV. Hình chữ nhật

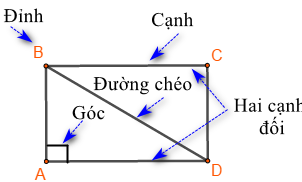
Hình chữ nhật \(ABCD\) có:

- Bốn đỉnh A, B, C, D

- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,\,BC = AD\).

- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.

- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.

- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường

Chu vi của hình chữ nhật là: \(C = 2\left( {a + b} \right);\)

Diện tích của hình chữ nhật là: \(S = a.b\)

Trong đó a, b là chiều dài và chiều rộng của HCN.

V. Hình thang cân

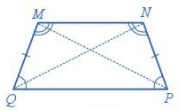
Hình thang cân \(MNPQ\) có:

Hai cạnh cạnh bên song song: \(MN\) song song với \(PQ\).

- Hai cạnh bên bằng nhau: \(MQ = NP\).

- Hai đường chéo bằng nhau: \(MP = NQ\).

- Hai góc kề với cạnh cạnh bên \(PQ\) bằng nhau.

- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó.

- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.

VI. Hình tam giác đều

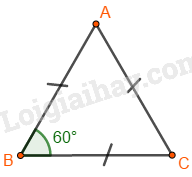
Tam giác đều \(ABC\) có:

+ Ba cạnh bằng nhau: \(AB = BC = CA\).

+ Ba góc ở các đỉnh \(A,B,\,C\) bằng nhau.

VII. Hình lục giác đều

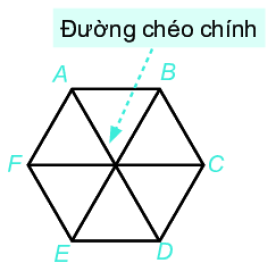
Lục giác đều \(ABCDEF\) có:

- Sáu đỉnh A, B, C, D, E, F

- Sáu cạnh bằng nhau: \(AB = BC = CD = DE = EF\).

- Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau.

- Ba đường chéo chính bằng nhau \(AD = BE = CF\).