Lý thuyết Lực từ - Cảm ứng từ

I. Lực Từ

Để dễ dàng khảo sát và đo đạc lực từ, trước hết ta khảo sát trong một từ trường đều.

1. Từ trường đều

Từ trường đều là từ trường mà đặc tính của nó giống nhau tại mọi điểm; các đường sức từ là những đường thẳng song song, cùng chiều và cách đều nhau.

2. Xác định lực từ do từ trường đều tác dụng lên một đoạn dây dẫn có dòng điện

Trong một từ trường đều có các đường sức từ thẳng đứng (tạo bởi một nam châm hình chữ U), ta đặt một đoạn dây dẫn M₁M₂ = l vuông góc với các đường sức từ. giả sử M₁M₂ được treo nằm ngang nhờ hai dây dẫn mảnh cùng độ dài O₁M₁ = O₂M₂, có hai đầu O₁ và O₂ dược giữ cố định. Dòng điện đi vào O₁ và ra O₂ qua dây dẫn M₁M₂ theo chiều từ M₁ đến M₂.

Khi cho dòng điện có cường độ I chạy qua M₁M₂ thì xuất hiện lực từ \(\overrightarrow{F}\) tác dụng lên M₁M₂. Thực nghiệm chứng tỏ rằng: \(\overrightarrow{F}\) ⊥ M₁M₂ và \(\overrightarrow{F}\) vuông góc với đường sức từ.

Kết quả \(\overrightarrow{F}\) có phương nằm ngang và có chiều như hình 20.1.

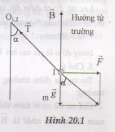
Dưới tác dụng của trọng lực mg và lực từ \(\overrightarrow{F}\), khi cân bằng \(m\overrightarrow{g}\) + \(\overrightarrow{F}\), tổng trực đối với lực căng \(\overrightarrow{T}\) của hai dây treo. Hai dây O₁M₁ và O₂M₂ lệch góc α so với phương thẳng đứng. Lực \(\overrightarrow{F}\) có cương độ được xác định bởi công thức:

\(\overrightarrow{F}\) = mgtanα.               (20.1)

II. Cảm ứng từ

1. Thí nghiệm: mô tả ở mục trên cho phép xác định lực từ \(\overrightarrow{F}\) do từ trường tác dụng lên đoạn dây dẫn M₁M₂ = l có dòng điện cường độ I chạy qua.

Tiến hành thí nghiệm trong đó cho I và l thay đổi, kết quả cho thấy thương số \(\frac{F}{Il}\)không thay đổi. thương số đó chỉ phụ thuộc vào tác dụng của từ trường tại vị trí đặt đoạn dây dẫn M₁M₂. Nói cách khác, có thể coi thương số đó đặc trưng cho tác dụng của từ trường tại vị trí khảo sát. Người ta định nghĩa thương số đó là cảm ứng từ tại vị trí khảo sát. Người ta định nghĩa thương số đó là cảm ứng từ tại vị trí đang xét, ký hiệu là B: 

B = \(\frac{F}{Il}\)                         (20.2)

2. Đơn vị cảm ứng từ

Trong hệ SI, đơn vị cảm ứng từ B là tesla (T). Trong công thức (20.2), F đo bằng niutơn (N), I đo bằng ampe (A) và l đo bằng mét (m).

3. Vectơ cảm ứng từ

Người ta biểu diễn cảm ứng từ bằng một vectơ gọi là vectơ cảm ứng từ, ký hiệu là \(\overrightarrow{B}\)

Vectơ cảm ứng từ \(\overrightarrow{B}\) tại một điểm:

-Có hướng trùng với hướng của từ trường tại điểm đó;

-Có độ lớn bằng: B = \(\frac{F}{Il}\)       

4. Biểu thức tổng quát của lực từ

Trước hết, ta định nghĩa Vectơ phần tử dòng điện I\(\overrightarrow{l}\) là véc tơ \(I\widehat{M_{1}M_{2}}\), cùng hướng với dòng điện và có độ lớn băng Il. Dựa vào những kết quả thực nghiệm đã nêu ở trên, có thể xác định lực từ \(\overrightarrow{F}\) tác dụng lên một phần tử dòng điện \(I\widehat{M_{1}M_{2}}\) = I\(\overrightarrow{l}\) khi đặt trong một từ trường đều, cảm ứng từ là \(\overrightarrow{B}\):

Lực từ \(\overrightarrow{F}\) có điểm đặt tại trung điểm của M₁M₂, có phương vuông góc với \(\overrightarrow{l}\) và \(\overrightarrow{B}\), có chiều tuân theo quy tắc bàn tay trái và có độ lớn:

F = IlBsinα

Trong đó α là góc tạo bởi \(\overrightarrow{B}\) và \(\overrightarrow{l}\).

5. Chú ý

Tương tự điện trường từ trường cũng tuân theo nguyên lí chồng chất từ trường:

Giả sử hệ có n nam châm (hay dòng điện). Tại điểm M, từ trường chỉ của nam châm thứ nhất là \(\overrightarrow{B_{1}}\), từ trường chỉ của nam châm thứ hai là \(\overrightarrow{B_{2}}\),…từ trường chỉ của nam châm thứ n là \(\overrightarrow{B_{n}}\). Gọi \(\overrightarrow{B}\) là từ trường của hệ tại M thì:

\(\overrightarrow{B}=\overrightarrow{B_{1}}+\overrightarrow{B_{2}}+...+\overrightarrow{B_{n}}\).